【題目】某小龍蝦養(yǎng)殖大戶為了更好地發(fā)揮技術優(yōu)勢，一次性收購了20000kg小龍蝦，計劃養(yǎng)殖一段時間后再出售．已知每天放養(yǎng)的費用相同，放養(yǎng)10天的總成本為30.4萬元；放養(yǎng)20天的總成本為30.8萬元（總成本=放養(yǎng)總費用+收購成本）．
（1）設每天的放養(yǎng)費用是a萬元，收購成本為b萬元，求a和b的值；
（2）設這批小龍蝦放養(yǎng)t天后的質量為m（kg），銷售單價為y元/kg．根據(jù)以往經驗可知：m與t的函數(shù)關系為
；y與t的函數(shù)關系如圖所示．
①分別求出當0≤t≤50和50＜t≤100時，y與t的函數(shù)關系式；
②設將這批小龍蝦放養(yǎng)t天后一次性出售所得利潤為W元，求當t為何值時，W最大？并求出最大值．（利潤=銷售總額﹣總成本）
【答案】（1）a的值為0.04，b的值為30；（2）①當0≤t≤50時，
，當50＜t≤100時，
；（3）放養(yǎng)55天時，W最大，最大值為180250元．
【解析】
（1）由放養(yǎng)10天的總成本為30.4萬元；放養(yǎng)20天的總成本為30.8萬元可得答案；
（2）①分0≤t≤50、50<t≤100兩種情況，結合函數(shù)圖象利用待定系數(shù)法求解可得；
②就以上兩種情況，根據(jù)“利潤=銷售總額-總成本”列出函數(shù)解析式，依據(jù)一次函數(shù)性質和二次函數(shù)性質求得最大值即可得．
（1）由題意，得：
，解得：
．
答：a的值為0.04，b的值為30．
（2）①當0≤t≤50時，設y與t的函數(shù)解析式為
，將（0，15）、（50，25）代入，得：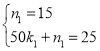
，解得：
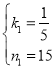，∴y與t的函數(shù)解析式為
當50＜t≤100時，設y與t的函數(shù)解析式為
，將點（50，25）、（100，20）代入，得：
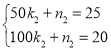，解得：
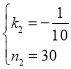，∴y與t的函數(shù)解析式為
②由題意，當0≤t≤50時，W=20000（
t+15）﹣（400t+300000）=3600t．
∵3600＞0，∴當t=50時，W最大值=180000（元）；
當50＜t≤100時，W=（100t+15000）（﹣
t+30）﹣（400t+300000）
=﹣10t2+1100t+150000=﹣10（t﹣55）2+180250．
∵﹣10＜0，∴當t=55時，W最大值=180250（元）．
綜上所述：放養(yǎng)55天時，W最大，最大值為180250元．
科目：初中數(shù)學 來源： 題型：
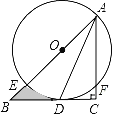
【題目】如圖，在Rt△ABC中，∠C＝90°，AD平分∠BAC，交BC于點D，點O在AB上，⊙O經過A，D兩點，交AB于點E，交AC于點F
（1）求證：BC是⊙O的切線；
（2）若⊙O半徑是2cm，F是弧AD的中點，求陰影部分的面積（結果保留π和根號）
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
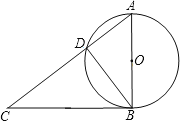
【題目】如圖，Rt△ABC中，∠ABC＝90°，以AB為直徑作⊙O交AC于點D，連接BD．
（1）求證：∠A＝∠CBD．
（2）若AB＝10，AD＝6，M為線段BC上一點，請寫出一個BM的值，使得直線DM與⊙O相切，并說明理由．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】下圖是學習分式方程應用時，老師板書的問題和兩名同學所列的方程．
根據(jù)以上信息，解答下列問題：
（1）甲同學所列方程中的
表示_________________；乙同學所列方程中的
表示________________；
（2）兩個方程中任選一個，解方程并回答老師提出的問題．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】為了了解某區(qū)的綠化進程，小明同學查詢了園林綠化政務網，根據(jù)網站發(fā)布的近幾年該城市城市綠化資源情況的相關數(shù)據(jù)，繪制了如下統(tǒng)計圖（不完整）
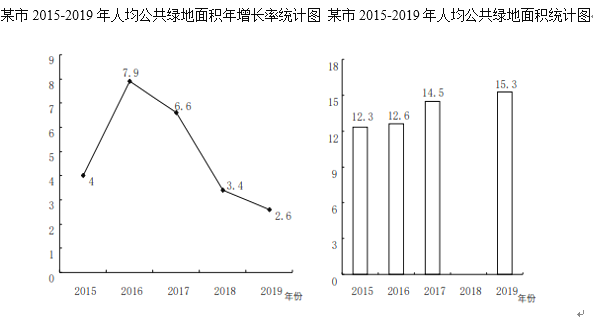
請根據(jù)以上信息解答下列問題：
求2018年該市人均公共綠地面積是多少平方米(精確到
？
補全條形統(tǒng)計圖；
小明同學還了解到自己身邊的許多同學都樹立起了綠色文明理念，從自身做起，多種樹，為提高人均公共綠地面積做貢獻，他對所在班級的多
名同學2019年參與植樹的情況做了調查，并根據(jù)調查情況繪制出如下統(tǒng)計表：
種樹棵數(shù)（棵） |
|
|
|
|
|
|
人數(shù) |
|
|
|
|
|
|
如果按照小明的統(tǒng)計數(shù)據(jù)，請你通過計算估計，他所在學校的
名同學在2019年共植樹多少棵？
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】“校園安全”越來越受到人們的關注，我市某中學對部分學生就校園安全知識的了解程度，采用隨機抽樣調查的方式，并根據(jù)收集到的信息進行統(tǒng)計，繪制了下面兩幅尚不完整的統(tǒng)計圖．根據(jù)圖中信息回答下列問題：
（1）接受問卷調查的學生共有______人，條形統(tǒng)計圖中m的值為______；
（2）扇形統(tǒng)計圖中“了解很少”部分所對應扇形的圓心角的度數(shù)為______；
（3）若該中學共有學生1800人，根據(jù)上述調查結果，可以估計出該學校學生中對校園安全知識達到“非常了解”和“基本了解”程度的總人數(shù)為______人；
（4）若從對校園安全知識達到“非常了解”程度的2名男生和2名女生中隨機抽取2人參加校園安全知識競賽，請用列表或畫樹狀圖的方法，求恰好抽到1名男生和1名女生的概率．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知△ABC的三個頂點坐標分別是A（1，1），B（4，1），C（3，3）．
（1）將△ABC向下平移5個單位后得到△A1B1C1，請畫出△A1B1C1；
（2）將△ABC繞原點O逆時針旋轉90°后得到△A2B2C2，請畫出△A2B2C2；
（3）判斷以O，A1，B為頂點的三角形的形狀．（無須說明理由）
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，矩形ABCD長與寬的比為3：2，點E，F分別在邊AB、BC上，tan∠1＝
，tan∠2＝
，則cos（∠1+∠2）＝（ ）
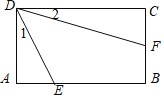
A.
B.
C.
D.1
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
