
【題目】(10分)已知△ABC是等邊三角形,點D是直線BC上一點,以AD為一邊在AD的右側作等邊△ADE.
(1)如圖①,點D在線段BC上移動時,直接寫出∠BAD和∠CAE的大小關系;
(2)如圖②,點D在線段BC的延長線上移動時,猜想∠DCE的大小是否發生變化.若不變請求出其大小;若變化,請說明理由.

【答案】(1)∠BAD=∠CAE;(2)∠DCE=60°,不發生變化.
【解析】試題分析:(1)由等邊三角形的性質得出∠BAC=∠DAE,容易得出結論;
(2)由△ABC和△ADE是等邊三角形可以得出AB=BC=AC,AD=AE,∠ABC=∠ACB=∠BAC=∠DAE=60°,得出∠ABD=120°,再證明△ABD≌△ACE,得出∠ABD=∠ACE=120°,即可得出結論;
解:(1)∠BAD=∠CAE;理由:
∵△ABC和△ADE是等邊三角形,
∴∠BAC=∠DAE=60°,
∴∠BAD=∠CAE;
(2)∠DCE=60°,不發生變化;理由如下:
∵△ABC是等邊三角形,△ADE是等邊三角形,
∴∠DAE=∠BAC=∠ABC=∠ACB=60°,AB=AC,AD=AE.
∴∠ABD=120°,∠BAC﹣∠BAE=∠DAE﹣∠BAE
∴∠DAB=∠CAE.
在△ABD和△ACE中,
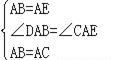 ,
,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠ABD=120°.
∴∠DCE=∠ACE﹣∠ACB=120°﹣60°=60°.
點睛:本題考查了全等三角形的判定與性質以及等邊三角形的性質;熟練掌握等邊三角形的性質,證明三角形全等是解決問題的關鍵.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:
【題目】小明在學了三角形的角平分線后,遇到下列4個問題,請你幫他解決.如圖,在△ABC中,∠BAC= 50°,點I是∠ABC、∠ACB平分線的交點.

問題(1):填空:∠BIC=_________°.
問題(2):若點D是兩條外角平分線的交點,則∠BDC=_________°.
問題(3):若點E是內角∠ABC、外角∠ACG的平分線的交點,則∠BEC與∠BAC的數量關系是________;
問題(4):在問題(3)的條件下,當∠ACB等于__________°時,CE∥AB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() ,
, ![]() ,點
,點![]() 點
點![]() 分別在射線
分別在射線![]() ,射線
,射線![]() 上,若點
上,若點![]() 與點
與點![]() 關于
關于![]() 對稱,點
對稱,點![]() 點
點![]() 關于
關于![]() 對稱,
對稱, ![]() 與
與![]() 相交于點
相交于點![]() ,有以下命題:①
,有以下命題:①![]() ;②
;②![]() ;③若
;③若![]() ,
, ![]() ;④
;④![]() 是等腰直角三角形,則正確的命題有( ).
是等腰直角三角形,則正確的命題有( ).

A. ![]() 個 B.
個 B. ![]() 個 C.
個 C. ![]() 個 D.
個 D. ![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示:∠AOB的內部有一點P,到頂點O的距離為5cm,M、N分別是射線OA、OB上的動點.若∠AOB =30![]() ,則△PMN周長的最小值為________.
,則△PMN周長的最小值為________.
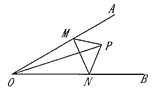
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀下面的內容,再解決問題.
例題:若![]() , 求m和n的值
, 求m和n的值
解:∵![]()
∴![]()
∴![]()
∴![]() ,
, ![]()
∴![]() ,
, ![]()
問題:(1)若![]() ,求
,求![]() 的值.
的值.
(2)已知a,b,c是△ABC的三邊長,滿足![]() ,且c是△ABC中最長的邊,求c的取值范圍.
,且c是△ABC中最長的邊,求c的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在八年級(1)班學生中開展對于“我國國家公祭日”知曉情況的問卷調查.
問卷調查的結果分為A、B、C、D四類,其中A類表示“非常了解”;B類表示“比較了解”;C類表示“基本了解”;D類表示“不太了解”;班長將本班同學的調查結果繪制成下列兩幅不完整的統計圖.

請根據上述信息解答下列問題:
(1)該班參與問卷調查的人數有 人;補全條形統計圖;
(2)求出C類人數占總調查人數的百分比及扇形統計圖中![]() 類所對應扇形圓心角的度數.
類所對應扇形圓心角的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠MON=30°,點A1,A2,A3,…在射線ON上,點B1,B2,B3,…在射線OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均為等邊三角形,若OA1=2,則△A5B5A6的邊長為( )

A. 8 B. 16 C. 24 D. 32
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某特產專賣店銷售核桃,其進價為每千克40元,按每千克60元出售,平均每天可售出100千克,后來經過市場調查發現,單價每降低2元,則平均每天的銷售可增加20千克,若該專賣店銷售這種核桃要想平均每天獲利2240元,請回答:
(1)每千克核桃應降價多少元?
(2)在平均每天獲利不變的情況下,為盡可能讓利于顧客,贏得市場,該店應按原售價的幾折出售?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com