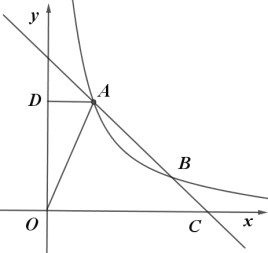
【題目】如圖，一次函數
的圖象與反比例函數
在第一象限的圖象交于
和B兩點，與x軸交于點C．
（1）求反比例函數的解析式及點C的坐標.
（2）求△OCA的面積
【答案】(1) 
,C(3.0);(2) 3.
【解析】
（1）先把點A代入一次函數解析式求出a,再把點A代入反比例函數的解析式即可求出k,即可求出反比例函數解析式;令一次函數y=0,可求出C的坐標.
（2）連接OA,過點A作
于點D, 先算出△OCE和△OAE的面積,所求面積就是△OCE的面積-△OAE的面積,即可求得結果.
（1）由題可知點A既在一次函數圖象上,又在反比例函數圖象上,把點
代入
中,得
,
∴
,
把點A代入
中，得到k=2.
∴反比例函數的解析式為.
由圖可知,點C是一次函數圖象與x軸的交點,令一次函數y=0,可得x=3,
∴
.
∴反比例函數的解析式為,C點的坐標為
.
（2）如圖,連接OA,過點A作于點D,
由（1）可得,
∴AD=1,
由圖可知,E點是一次函數與y軸的交點,
∴
,
∴OE=3,
又∵OC=3,
∴
,
,
∴
.
所以△OCA的面積是3.
科目：初中數學 來源： 題型：
【題目】如圖，方格紙中每個小正方形的邊長都是1個單位長度，△ABC在平面直角坐標系中的位置如圖所示．
（1）將△ABC向上平移3個單位后，得到△A1B1C1，請畫出△A1B1C1，并直接寫出點A1的坐標．
（2）將△ABC繞點O順時針旋轉90°，請畫出旋轉后的△A2B2C2，并求點B所經過的路徑長（結果保留π）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=5，AD=4，BD=DC=3，且DE⊥AB于E，DF⊥AC于點F．
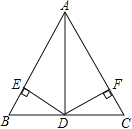
（1）請寫出與A點有關的三個正確結論；
（2）DE與DF在數量上有何關系？并給出證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，PA、PB為⊙O的切線，M、N是PA、AB的中點，連接MN交⊙O點C，連接PC交⊙O于D，連接ND交PB于Q，求證：MNQP為菱形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲，乙兩輛汽車分別從A，B兩地同時出發(fā)，沿同一條公路相向而行，乙車出發(fā)2h后休息，與甲車相遇后，繼續(xù)行駛．設甲、乙兩車與B地的路程分別為y甲（km），y乙（km），甲車行駛的時間為x（h），y甲，y乙與x之間的函數圖象如圖所示，結合圖象解答下列問題：
（1）乙車休息了 _________ h；
（2）求乙車與甲車相遇后y乙與x的函數解析式，并寫出自變量x的取值范圍；．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，觀察數軸，請回答：
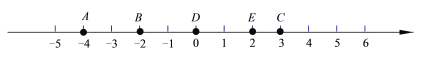
（1）點C與點D的距離為______ ，點B與點D的距離為______ ；
（2）點B與點E的距離為______ ，點A與點C的距離為______ ；
發(fā)現：在數軸上，如果點M與點N分別表示數m，n，則他們之間的距離可表示為 ______（用m，n表示）
（3）利用發(fā)現的結論解決下列問題： 數軸上表示x的點P與B之間的距離是1，則 x 的值是______ ．
查看答案和解析>>
科目：初中數學 來源： 題型：
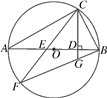
【題目】如圖，已知AB是⊙O的直徑，點C是⊙O上一點，連接BC，AC，過點C作直線CD⊥AB于點D，點E是AB上一點，直線CE交⊙O于點F，連接BF與直線CD延長線交于點G.求證：BC2＝BG·BF.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知如圖，在菱形ABCD中，對角線AC、BD相交于點O，DE∥AC，AE∥BD．
（1）求證：四邊形AODE是矩形；
（2）若AB=12，∠BCD=120°，求四邊形AODE的面積
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，點D、E、F分別在AB、BC、AC邊上，已知DE﹦DF，∠EDF＝∠A。
（1）找出圖中相似的三角形，并證明；
（2）求證： 
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com