【題目】依據下列解方程
的過程，請在前面括號內填寫變形步驟，在后面的括號內填寫變形依據.
解：原方程可變形為
，
去分母，得
.(____________________)
去括號，得
.(____________________)
移項，得
.(____________________)
合并，得
.(合并同類項）
(______)，得
.（______________）
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖,在平面直角坐標系中,以A(3,0)為圓心,以5為半徑的圓與x軸相交于B. C,與y軸的負半軸相交于D,拋物線y=x
+bx+c經過B. C. D三點。
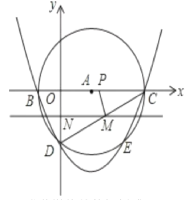
(1)求此拋物線的解析式；
(2)若動直線MN(MN∥x軸)從點D開始，以每秒1個長度單位的速度沿y軸的正方向移動，且與線段CD、y軸分別交于M、N兩點，動點P同時從點C出發，在線段OC上以每秒2個長度單位的速度向原點O運動，連接PM，設運動時間為t秒，若以P、C. M為頂點的三角形與△OCD相似，求實數t的值；
②當t為何值時,
的值最大，并求出最大值。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】矩形紙片ABCD中，已知AD=8，AB=6，E是邊BC上的點，以AE為折痕折疊紙片，使點B落在點F處，連接FC，當△EFC為直角三角形時，BE的長為 ．
【答案】3或6
【解析】試題分析：
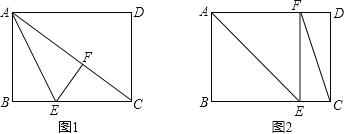
由題意可知有兩種情況，見圖1與圖2；
圖1：當點F在對角線AC上時，∠EFC=90°，
∵∠AFE=∠B=90°，∠EFC=90°，
∴點A、F、C共線，
∵矩形ABCD的邊AD=8，
∴BC=AD=8，
在Rt△ABC中，AC=
=10，
設BE=x，則CE=BC﹣BE=8﹣x，
由翻折的性質得，AF=AB=6，EF=BE=x，
∴CF=AC﹣AF=10﹣6=4，
在Rt△CEF中，EF2+CF2=CE2，
即x2+42=（8﹣x）2，
解得x=3，
即BE=3；
圖2：當點F落在AD邊上時，∠CEF=90°，
由翻折的性質得，∠AEB=∠AEF=
×90°=45°，
∴四邊形ABEF是正方形，
∴BE=AB=6，
綜上所述，BE的長為3或6．
故答案為：3或6．
考點：1、軸對稱（翻折變換）；2、勾股定理
【題型】填空題
【結束】
15
【題目】計算：(
)﹣2﹣
+（
﹣4）0﹣
cos45°．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對于任意四個有理數a，b，c，d，可以組成兩個有理數對（a，b）與（c，d）．我們規定：
（a，b）★（c，d）=bc－ad．
例如：（1，2）★（3，4）=2×3－1×4=2．
根據上述規定解決下列問題：
（1）有理數對（2，－3）★（3，－2）=_______；
（2）若有理數對（－3，2x－1）★（1，x+1）=7，則x=_______；
（3）當滿足等式（－3，2x－1）★（k，x＋k）=5＋2k的x是整數時，求整數k的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在□ABCD中，點E、F、G、H分別在邊AB、BC、CD、DA上，AE＝CG，AH＝CF．
（1）求證：△AEH≌△CGF；
（2）若EG平分∠HEF，求證：四邊形EFGH是菱形．
查看答案和解析>>
科目：初中數學 來源： 題型：
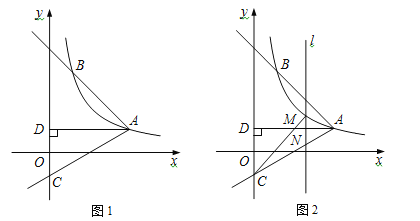
【題目】如圖1，反比例函數
（x＞0）的圖象經過點A（
，1），射線AB與反比例函數圖象交于另一點B（1，a），射線AC與y軸交于點C，∠BAC＝75°，AD⊥y軸，垂足為D．
（1）求k的值；
（2）求tan∠DAC的值及直線AC的解析式；
（3）如圖2，M是線段AC上方反比例函數圖象上一動點，過M作直線l⊥x軸，與AC相交于點N，連接CM，求△CMN面積的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某研究性學習小組進行了探究活動．如圖，已知一架竹梯AB斜靠在墻角MON處，竹梯AB=13m，梯子底端離墻角的距離BO=5m．
（1）求這個梯子頂端A距地面有多高；
（2）如果梯子的頂端A下滑4 m到點C，那么梯子的底部B在水平方向上滑動的距離BD=4 m嗎？為什么？
（3）亮亮在活動中發現無論梯子怎么滑動，在滑動的過程中梯子上總有一個定點到墻角O的距離始終是不變的定值，會思考問題的你能說出這個點并說明其中的道理嗎？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在一張長為7cm，寬為5cm的矩形紙片上，現在剪下一個腰長為4cm的等腰三角形，要求等腰三角形的一個頂點與矩形的一個頂點重合，其余的兩個頂點在矩形的邊上，則剪下的等腰三角形一腰上的的高為_____________。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2014年1月，國家發改委出臺指導意見，要求2015年底前，所有城市原則上全面實行居民階梯水價制度．小明為了解市政府調整水價方案的社會反響，隨機訪問了自己居住小區的部分居民，就“每月每戶的用水量”和“調價對用水行為改變”兩個問題進行調查，并把調查結果整理繪制成下面的統計圖（圖1，圖2）．
小明發現每月每戶的用水量在5m3-35m3之間，有8戶居民對用水價格調價漲幅抱無所謂，不會考慮用水方式的改變，根據小明繪制的圖表和發現的信息，完成下列問題：
（Ⅰ）n= ，小明調查了 戶居民，并補全圖2；
（Ⅱ）每月每戶用水量的中位數和眾數分別落在什么范圍？
（Ⅲ）如果小明所在小區有1800戶居民，請你估計“視調價漲幅采取相應的用水方式改變”的居民戶數有多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
