
【題目】如圖1,反比例函數![]() (x>0)的圖象經過點A(
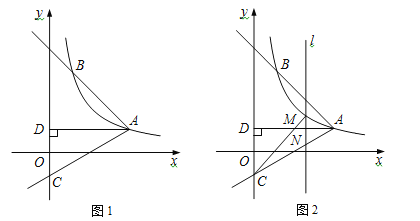
(x>0)的圖象經過點A(![]() ,1),射線AB與反比例函數圖象交于另一點B(1,a),射線AC與y軸交于點C,∠BAC=75°,AD⊥y軸,垂足為D.
,1),射線AB與反比例函數圖象交于另一點B(1,a),射線AC與y軸交于點C,∠BAC=75°,AD⊥y軸,垂足為D.
(1)求k的值;
(2)求tan∠DAC的值及直線AC的解析式;
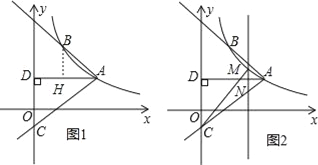
(3)如圖2,M是線段AC上方反比例函數圖象上一動點,過M作直線l⊥x軸,與AC相交于點N,連接CM,求△CMN面積的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]()
【解析】試題分析:(1)根據反比例函數圖象上點的坐標特征易得k=2![]() ;
;
(2)作BH⊥AD于H,如圖1,根據反比例函數圖象上點的坐標特征確定B點坐標為(1,2![]() ),則AH=2
),則AH=2![]() ﹣1,BH=2
﹣1,BH=2![]() ﹣1,可判斷△ABH為等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC﹣∠BAH=30°,根據特殊角的三角函數值得tan∠DAC=
﹣1,可判斷△ABH為等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC﹣∠BAH=30°,根據特殊角的三角函數值得tan∠DAC=![]() ;由于AD⊥y軸,則OD=1,AD=2
;由于AD⊥y軸,則OD=1,AD=2![]() ,然后在Rt△OAD中利用正切的定義可計算出CD=2,易得C點坐標為(0,﹣1),于是可根據待定系數法求出直線AC的解析式為y=
,然后在Rt△OAD中利用正切的定義可計算出CD=2,易得C點坐標為(0,﹣1),于是可根據待定系數法求出直線AC的解析式為y=![]() x﹣1;
x﹣1;
(3)利用M點在反比例函數圖象上,可設M點坐標為(t,![]() )(0<t<2
)(0<t<2![]() ),由于直線l⊥x軸,與AC相交于點N,得到N點的橫坐標為t,利用一次函數圖象上點的坐標特征得到N點坐標為(t,
),由于直線l⊥x軸,與AC相交于點N,得到N點的橫坐標為t,利用一次函數圖象上點的坐標特征得到N點坐標為(t,![]() t﹣1),則MN=
t﹣1),則MN=![]() ﹣
﹣![]() t+1,根據三角形面積公式得到S△CMN=
t+1,根據三角形面積公式得到S△CMN=![]() t(
t(![]() ﹣
﹣![]() t+1),再進行配方得到S=﹣
t+1),再進行配方得到S=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() (0<t<2
(0<t<2![]() ),最后根據二次函數的最值問題求解.
),最后根據二次函數的最值問題求解.
試題解析:(1)把A(2![]() ,1)代入y=
,1)代入y=![]() ,得k=2
,得k=2![]() ×1=2
×1=2![]() ;
;
(2)作BH⊥AD于H,如圖1,
把B(1,a)代入反比例函數解析式y=![]() ,得a=2
,得a=2![]() ,
,
∴B點坐標為(1,2![]() ),
),
∴AH=2![]() ﹣1,BH=2
﹣1,BH=2![]() ﹣1,
﹣1,
∴△ABH為等腰直角三角形,∴∠BAH=45°,
∵∠BAC=75°,∴∠DAC=∠BAC﹣∠BAH=30°,
∴tan∠DAC=tan30°=![]() ;
;
∵AD⊥y軸,∴OD=1,AD=2![]() ,∵tan∠DAC=
,∵tan∠DAC=![]() =
=![]() ,
,
∴CD=2,∴OC=1,
∴C點坐標為(0,﹣1),
設直線AC的解析式為y=kx+b,
把A(2![]() ,1)、C(0,﹣1)代入得
,1)、C(0,﹣1)代入得![]() ,解得
,解得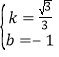 ,
,
∴直線AC的解析式為y=![]() x﹣1;
x﹣1;
(3)設M點坐標為(t,![]() )(0<t<2
)(0<t<2![]() ),
),
∵直線l⊥x軸,與AC相交于點N,∴N點的橫坐標為t,∴N點坐標為(t,![]() t﹣1),
t﹣1),
∴MN=![]() ﹣(
﹣(![]() t﹣1)=
t﹣1)=![]() ﹣
﹣![]() t+1,
t+1,
∴S△CMN=![]() t(
t(![]() ﹣
﹣![]() t+1)=﹣
t+1)=﹣![]() t2+
t2+![]() t+
t+![]() =﹣
=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() (0<t<2
(0<t<2![]() ),
),
∵a=﹣![]() <0,∴當t=
<0,∴當t=![]() 時,S有最大值,最大值為
時,S有最大值,最大值為![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,∠BAD的平分線交BC于點E,∠ABC的平分線交AD于點F.若BF=12,AB=10,則AE的長為( )

A. 10 B. 12 C. 16 D. 18
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中考體育測試前,某區教育局為了了解選報引體向上的初三男生的成績情況,隨機抽測了本區部分選報引體向上項目的初三男生的成績,并將測試得到的成績繪成了下面兩幅不完整的統計圖:
請你根據圖中的信息,解答下列問題:
(![]() )寫出扇形圖中
)寫出扇形圖中![]() __________
__________![]() ,并補全條形圖.
,并補全條形圖.
(![]() )在這次抽測中,測試成績的眾數和中位數分別是__________個、__________個.
)在這次抽測中,測試成績的眾數和中位數分別是__________個、__________個.
(![]() )該區體育中考選報引體向上的男生共有
)該區體育中考選報引體向上的男生共有![]() 人,如果體育中考引體向上達
人,如果體育中考引體向上達![]() 個以上(含
個以上(含![]() 個)得滿分,請你估計該區體育中考中選報引體向上的男生能獲得滿分的有多少名?
個)得滿分,請你估計該區體育中考中選報引體向上的男生能獲得滿分的有多少名?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】依據下列解方程![]() 的過程,請在前面括號內填寫變形步驟,在后面的括號內填寫變形依據.
的過程,請在前面括號內填寫變形步驟,在后面的括號內填寫變形依據.
解:原方程可變形為![]() ,
,
去分母,得![]() .(____________________)
.(____________________)
去括號,得![]() .(____________________)
.(____________________)
移項,得![]() .(____________________)
.(____________________)
合并,得![]() .(合并同類項)
.(合并同類項)
(______),得![]() .(______________)
.(______________)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
![]() ,
,![]() ,
,![]() ,
,
由以上三個等式相加,可得
![]()
![]() .
.
讀完以上材料,請你計算下列各題:
(1)![]() (寫出過程);
(寫出過程);
(2)![]() __________________________(直接寫出答案);
__________________________(直接寫出答案);
(3)![]() _____________________(直接寫出答案).
_____________________(直接寫出答案).
查看答案和解析>>
科目:初中數學 來源: 題型:
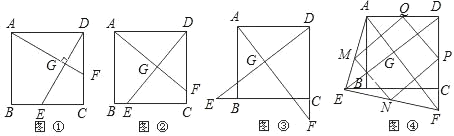
【題目】如圖1,在正方形ABCD中,點E、F分別為邊BC、CD的中點,AF、DE相交于點G,則可得結論:①AF=DE,②AF⊥DE(不須證明).
(1)如圖②,若點E、F不是正方形ABCD的邊BC、CD的中點,但滿足CE=DF,則上面的結論①、②是否仍然成立;(請直接回答“成立”或“不成立”)
(2)如圖③,若點E、F分別在正方形ABCD的邊CB的延長線和DC的延長線上,且CE=DF,此時上面的結論①、②是否仍然成立?若成立,請寫出證明過程;若不成立,請說明理由.
(3)如圖④,在(2)的基礎上,連接AE和EF,若點M、N、P、Q分別為AE、EF、FD、AD的中點,請先判斷四邊形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一種,并寫出證明過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2014年1月,國家發改委出臺指導意見,要求2015年底前,所有城市原則上全面實行居民階梯水價制度.小明為了解市政府調整水價方案的社會反響,隨機訪問了自己居住在小區的部分居民,就“每月每戶的用水量”和“調價對用水行為改變”兩個問題進行調查,并把調查結果整理成下面的圖1,圖2.

小明發現每月每戶的用水量在5m2-35m2之間,有8戶居民對用水價格調價漲幅抱無所謂,不用考慮用水方式的改變.根據小明繪制的圖表和發現的信息,完成下列問題:
(1)n= ,小明調查了 戶居民,并補全圖1;
(2)每月每戶用水量的中位數和眾數分別落在什么范圍?
(3)如果小明所在的小區有1800戶居民,請你估計“視調價漲幅采取相應的用水方式改變”的居民戶數有多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出以下命題:
①函數![]() 是偶函數,但不是奇函數;
是偶函數,但不是奇函數;
②已知回歸直線方程為![]() ,樣本點的中心為
,樣本點的中心為![]() ,則
,則![]() ;
;
③函數![]() 圖象關于點
圖象關于點![]() 對稱且在
對稱且在![]() 上單調遞增;
上單調遞增;
④根據黨中央關于“精準”脫貧的要求,我州某農業經濟部門決定派出五位相關專家對三個貧困地區進行調研,每個地區至少派遣一位專家,其中甲、乙兩位專家需要派遣至同一地區,則不同的派遣方案種數有![]() 種;
種;
⑤已知雙曲線![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,過
,過![]() 的直線交雙曲線右支于
的直線交雙曲線右支于![]() 兩點,且
兩點,且![]() ,若
,若![]() ,則雙曲線的離心率為
,則雙曲線的離心率為![]() .
.
其中正確的命題序號為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com