
【題目】如圖,在![]() 中,
中,![]() ,以
,以![]() 為直徑作圓
為直徑作圓![]() ,分別交
,分別交![]() 于點
于點![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,連接
,連接![]() 交線段
交線段![]() 于點
于點![]() .
.

(1)求證:![]() 是圓
是圓![]() 的切線;
的切線;
(2)若![]() 為
為![]() 的中點,求
的中點,求![]() 的值;
的值;
(3)若![]() ,求圓
,求圓![]() 的半徑.
的半徑.
【答案】(1)見解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據同圓的半徑相等和等邊對等角證明:∠ODB=∠OBD=∠ACB,則DH⊥OD,DH是圓O的切線;
(2)如圖2,先證明∠E=∠B=∠C,則H是EC的中點,設AE=x,EC=4x,則AC=3x,由OD是△ABC的中位線,得:![]() ,證明△AEF∽△ODF,列比例式可得結論;
,證明△AEF∽△ODF,列比例式可得結論;
(3)如圖2,設⊙O的半徑為r,即OD=OB=r,證明DF=OD=r,則DE=DF+EF=r+1,BD=CD=DE=r+1,證明△BFD∽△EFA,列比例式為:![]() ,則
,則![]() ,求出r的值即可.
,求出r的值即可.
證明:(1)連接![]() 如圖1所示
如圖1所示
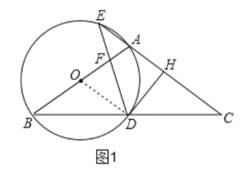
![]()
![]() 是等腰三角形
是等腰三角形
![]()
又在![]() 中
中![]()
![]()
由①②得: ![]()
![]()
![]()
![]()
![]() 是圓
是圓![]() 的切線
的切線
(2)如圖2,在圓![]() 中,
中,
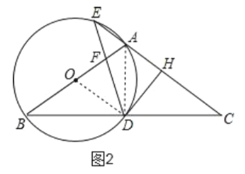
![]() ,
,
∴由(1)可知:![]() ,
,
![]() 是等腰三角形,
是等腰三角形,
![]() , 且點
, 且點![]() 是
是![]() 中點,
中點,
設![]() ,
,![]() ,則
,則![]() ,
,
連接![]() , 則在圓
, 則在圓![]() 中,
中,![]() ,
, ![]() ,
,
![]() ,
,
![]() 是
是![]() 的中點,
的中點,
![]() 是
是![]() 的中位線,
的中位線,
![]()
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
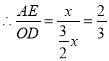
![]()
(3)如圖2,設![]() 的半徑為
的半徑為![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
則![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,![]() 是等腰三角形,
是等腰三角形,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
![]()
![]() ,
,
![]() ,
,
![]()
解得: ![]() ,
,![]() (舍)
(舍)
綜上所述, ![]() 的半徑為
的半徑為![]() .
.


科目:初中數學 來源: 題型:
【題目】在矩形![]() 中,
中,![]() ,將其沿對角線
,將其沿對角線![]() 折疊,頂點
折疊,頂點![]() 的對應點
的對應點![]() ,
,![]() 交
交![]() 于點
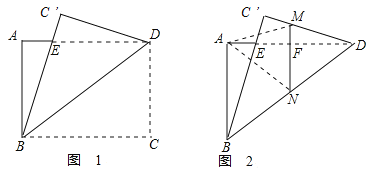
于點![]() 如圖1,再折疊,使點
如圖1,再折疊,使點![]() 落在
落在![]() 處,折痕
處,折痕![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,得到圖2,則折痕
,得到圖2,則折痕![]() 的長為____________.
的長為____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形![]() 的邊長為6,點
的邊長為6,點![]() 是
是![]() 的中點,連接
的中點,連接![]() 與對角線
與對角線![]() 交于點
交于點![]() ,連接
,連接![]() 并延長,交
并延長,交![]() 于點
于點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .以下結論:①
.以下結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正確結論的個數是( )
,其中正確結論的個數是( )
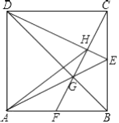
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
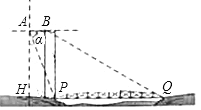
【題目】如圖示一架水平飛行的無人機AB的尾端點A測得正前方的橋的左端點P的
俯角為α其中tanα=2![]() ,無人機的飛行高度AH為500
,無人機的飛行高度AH為500![]() 米,橋的長度為1255米.
米,橋的長度為1255米.
①求點H到橋左端點P的距離;
②若無人機前端點B測得正前方的橋的右端點Q的俯角為30°,求這架無人機的長度AB.
查看答案和解析>>
科目:初中數學 來源: 題型:
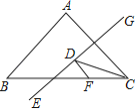
【題目】如圖,等腰△ABC的底邊BC=20,面積為120,點F在邊BC上,且BF=3FC,EG是腰AC的垂直平分線,若點D在EG上運動,則△CDF周長的最小值為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】事件發生的可能性有大有小,請你把下列事件發生可能性的大小按由小到大的順序排列起來__________.(只排序號)
①書包里有12本不同科目的教科書,隨手摸出一本,恰好是數學書;
②花2元買了一張彩票,就中了500萬大獎;
③我拋了兩次硬幣,都正面向上;
④若![]() ,則
,則![]() 和
和![]() 互為相反數.
互為相反數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,定義點P(x,y)的變換點為P′(x+y,x﹣y).
(1)如圖1,如果⊙O的半徑為![]() ,
,
①請你判斷M(2,0),N(﹣2,﹣1)兩個點的變換點與⊙O的位置關系;
②若點P在直線y=x+2上,點P的變換點P′在⊙O的內,求點P橫坐標的取值范圍.
(2)如圖2,如果⊙O的半徑為1,且P的變換點P′在直線y=﹣2x+6上,求點P與⊙O上任意一點距離的最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“機動車行駛到斑馬線要禮讓行人”等交通法規實施后,某校數學課外實踐小組就對這些交通法規的了解情況在全校隨機調查了部分學生,調查結果分為四種:A.非常了解,B.比較了解,C.基本了解,D.不太了解,實踐小組把此次調查結果整理并繪制成下面不完整的條形統計圖和扇形統計圖.
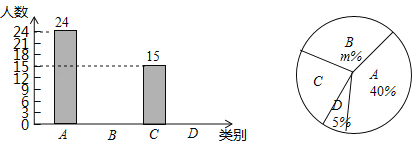
請結合圖中所給信息解答下列問題:
(1)填空:本次共調查_____名學生;扇形統計圖中C所對應扇形的圓心角度數是_____°;
(2)請直接補全條形統計圖;
(3)填空:扇形統計圖中,m的值為_____;
(4)該校共有500名學生,根據以上信息,請你估計全校學生中對這些交通法規“非常了解”的約有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,D為直線BC上一點,E為直線AC上一點,
,D為直線BC上一點,E為直線AC上一點,![]() ,設
,設![]() ,
,![]() .
.
(1)如圖1,若點D在線段C上,點E在線段AC上,![]() ,
,![]() ,則
,則![]() ______
______![]() ;
;![]() ________
________![]() .
.
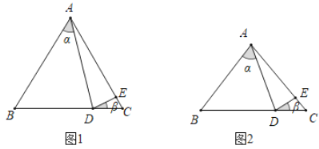
(2)如圖2,若點D在線段BC上,點E在線段AC上,則![]() ,
,![]() 之間有什么關系式?它說明理由.
之間有什么關系式?它說明理由.
(3)是否存在不同于(2)中的![]() ,
,![]() 之間的關系式?請寫出這個關系式(寫出一種即可),說明理由:若不存在,請說明理由.
之間的關系式?請寫出這個關系式(寫出一種即可),說明理由:若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com