
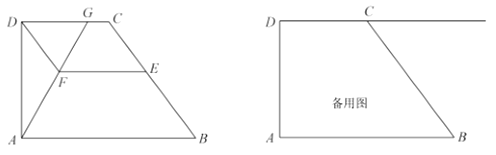
【題目】如圖,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是邊
是邊![]() 上一點(diǎn),過
上一點(diǎn),過![]() 、
、![]() 分別作
分別作![]() 、
、![]() 的平行線交于點(diǎn)
的平行線交于點(diǎn)![]() ,聯(lián)結(jié)
,聯(lián)結(jié)![]() 并延長,與射線
并延長,與射線![]() 交于點(diǎn)
交于點(diǎn)![]() .
.
(1)當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時,求
重合時,求![]() 的值;
的值;
(2)當(dāng)點(diǎn)![]() 在邊
在邊![]() .上時,設(shè)
.上時,設(shè)![]() ,求
,求![]() 的面積;(用含
的面積;(用含![]() 的代數(shù)式表示)
的代數(shù)式表示)
(3)當(dāng)![]() 時,求
時,求![]() 的余弦值.
的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由題意可得四邊形DCEF是平行四邊形,可得CD=EF,通過證明△CFE∽△CAB進(jìn)行分析求值即可;
(2)根據(jù)題意延長AG,BC交為于點(diǎn)M,過點(diǎn)C作CN⊥AB于點(diǎn)N,交EF于點(diǎn)H,由題意可得四邊形ADCN是矩形,可得AD=CN=4,CD=AN=3,BN=3,由平行線分線段成比例可求BE,ME,MC,CH,GC的長,即可求GD的長,由三角求形面積公式可△DFG的面積;
(3)根據(jù)題意由△AFD∽△ADG,可得∠AFD=∠ADG=90°,由余角的性質(zhì)可得∠DAG=∠B,即可求∠DAG的余弦值.
解:(1)如圖,
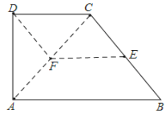
∵DC∥EF,DF∥CE,
∴四邊形DCEF是平行四邊形,
∴CD=EF,
∵AB=2CD=6,
∴AB=2EF,
∵EF∥CD,AB∥CD,
∴EF∥AB,
∴△CFE∽△CAB,
∴![]() ,
,
∴BC=2CE,
∴BE=CE,
∴EC:BE=1:1=1.
(2)如圖,延長AG,BC交為于點(diǎn)M,過點(diǎn)C作CN⊥AB于點(diǎn)N,交EF于點(diǎn)H,
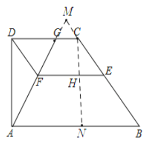
∵AD⊥CD,CN⊥CD,
∴AD∥CN,且CD∥AB,
∴四邊形ADCN是平行四邊形,
又∵∠DAB=90°,
∴四邊形ADCN是矩形,
∴AD=CN=4,CD=AN=3,
∴BN=AB-AN=3,
在Rt△BCN中,BC=![]() ,
,
∴BE=BC-CE=5-m,
∵EF∥AB,
∴![]() 即
即![]() ,
,
∴ME=BE=5-m,
∴MC=ME-CE=5-2m,
∵EF∥AB,
∴![]() ,
,
∴HC=![]() ,
,
∵CG∥EF,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)過點(diǎn)C作CN⊥AB于點(diǎn)N,
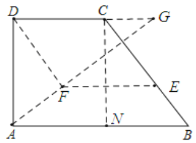
∵AB∥CD,∠DAB=90°,
∴∠DAB=∠ADG=90°,
若△AFD∽△ADG,
∴∠AFD=∠ADG=90°,
∴DF⊥AG,
又∵DF∥BC,
∴AG⊥BC,
∴∠B+∠GAB=90°,且∠DAG+∠GAB=90°,
∴∠B=∠DAG,
∴![]() .
.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,以
,以![]() 為直徑作圓
為直徑作圓![]() ,分別交
,分別交![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 的延長線于點(diǎn)
的延長線于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() 交線段
交線段![]() 于點(diǎn)
于點(diǎn)![]() .
.
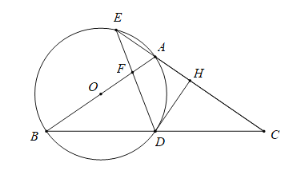
(1)求證:![]() 是圓
是圓![]() 的切線;
的切線;
(2)若![]() 為
為![]() 的中點(diǎn),求
的中點(diǎn),求![]() 的值;
的值;
(3)若![]() ,求圓
,求圓![]() 的半徑.
的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商場為了吸引顧客,設(shè)立了一個可以自由轉(zhuǎn)動的轉(zhuǎn)盤,如圖所示,并規(guī)定:顧客消費(fèi)200元(含200元)以上,就能獲得一次轉(zhuǎn)動轉(zhuǎn)盤的機(jī)會,如果轉(zhuǎn)盤停止后,指針正好對準(zhǔn)九折、八折、七折區(qū)域,顧客就可以獲得此項優(yōu)惠,如果指針恰好在分割線上時,則需重新轉(zhuǎn)動轉(zhuǎn)盤.
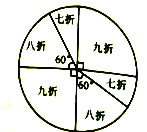
(1)某顧客正好消費(fèi)220元,他轉(zhuǎn)一次轉(zhuǎn)盤,他獲得九折、八折、七折優(yōu)惠的概率分別是多少?
(2)某顧客消費(fèi)中獲得了轉(zhuǎn)動一次轉(zhuǎn)盤的機(jī)會,實際付費(fèi)168元,請問他消費(fèi)所購物品的原價應(yīng)為多少元.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校在宣傳“民族團(tuán)結(jié)”活動中,采用四種宣傳形式:A.器樂,B.舞蹈,C.朗誦,D.唱歌.每名學(xué)生從中選擇并且只能選擇一種最喜歡的,學(xué)校就宣傳形式對學(xué)生進(jìn)行了抽樣調(diào)查,并將調(diào)查結(jié)果繪制了如下兩幅不完整的統(tǒng)計圖.
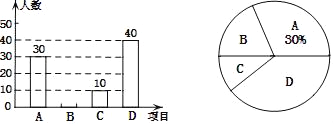
請結(jié)合圖中所給信息,解答下列問題:
(1)本次調(diào)查的學(xué)生共有_____人;
(2)補(bǔ)全條形統(tǒng)計圖;
(3)該校共有1200名學(xué)生,請估計選擇“唱歌”的學(xué)生有多少人?
(4)七年一班在最喜歡“器樂”的學(xué)生中,有甲、乙、丙、丁四位同學(xué)表現(xiàn)優(yōu)秀,現(xiàn)從這四位同學(xué)中隨機(jī)選出兩名同學(xué)參加學(xué)校的器樂隊,請用列表或畫樹狀圖法求被選取的兩人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,將
,將![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時針旋轉(zhuǎn)得到
逆時針旋轉(zhuǎn)得到![]() ,點(diǎn)
,點(diǎn)![]() 、
、![]() 分別與點(diǎn)
分別與點(diǎn)![]() 、
、![]() 對應(yīng),
對應(yīng),![]() 與邊
與邊![]() 交于點(diǎn)
交于點(diǎn)![]() .如果
.如果![]() ,那么
,那么![]() 的長是____________.
的長是____________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,D是邊BC的中點(diǎn),DE⊥AC,垂足為點(diǎn) E.
(1)求證:DECD=ADCE;
(2)設(shè)F為DE的中點(diǎn),連接AF、BE,求證:AFBC=ADBE.
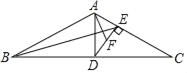
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】若一個三角形一條邊的平方等于另兩條的乘積,我們把這個三角形叫做比例三角形.
(1)已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,請直接寫出所有滿足條件的
,請直接寫出所有滿足條件的![]() 的長;
的長;
(2)如圖,在四邊形![]() 中,
中,![]() ,對角線
,對角線![]() 平分
平分![]() ,
,![]() .求證:
.求證:![]() 是比例三角形;
是比例三角形;
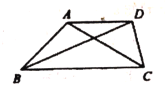
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 和
和![]() 是有公共頂點(diǎn)的直角三角形,
是有公共頂點(diǎn)的直角三角形,![]() ,點(diǎn)P為射線BD,CE的交點(diǎn).
,點(diǎn)P為射線BD,CE的交點(diǎn).
(1)如圖1,若![]() 和
和![]() 是等腰三角形,求證:
是等腰三角形,求證:![]() ;
;
(2)如圖2,若![]() ,問:(1)中的結(jié)論是否成立?請說明理由.
,問:(1)中的結(jié)論是否成立?請說明理由.
(3)在(1)的條件下,若![]() ,
,![]() ,若把
,若把![]() 繞點(diǎn)A旋轉(zhuǎn),當(dāng)
繞點(diǎn)A旋轉(zhuǎn),當(dāng)![]() 時,求PB的長.
時,求PB的長.
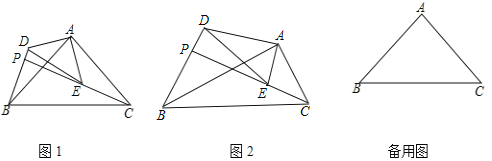
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】對于一個函數(shù),如果它的自變量 x 與函數(shù)值 y 滿足:當(dāng)1≤x≤1 時,1≤y≤1,則稱這個函數(shù)為“閉 函數(shù)”.例如:y=x,y=x 均是“閉函數(shù)”. 已知 y ax2 bx c(a0) 是“閉函數(shù)”,且拋物線經(jīng)過點(diǎn) A(1,1)和點(diǎn) B(1,1),則 a 的取值范圍是______________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com