
【題目】如圖,四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,PA=PD=CD=BC=1.
,PA=PD=CD=BC=1.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)見證明;(2)![]()
【解析】
(1)推導出AD⊥BD,PA⊥BD,從而BD⊥平面PAD,由此能證明平面PAD⊥平面ABCD.
(2)取AD中點O,連結PO,則PO⊥AD,以O為坐標原點,以過點O且平行于BC的直線為x軸,過點O且平行于AB的直線為y軸,直線PO為z軸,建立空間直角坐標系,利用空間向量法能求出直線PA與平面PBC所成角的正弦值.
(1)∵AB∥CD,∠BCD![]() ,PA=PD=CD=BC=1,
,PA=PD=CD=BC=1,
∴BD![]() ,∠ABC
,∠ABC![]() ,
,![]() ,∴
,∴![]() ,
,
∵AB=2,∴AD![]() ,∴AB2=AD2+BD2,∴AD⊥BD,
,∴AB2=AD2+BD2,∴AD⊥BD,
∵PA⊥BD,PA∩AD=A,∴BD⊥平面PAD,
∵BD平面ABCD,∴平面PAD⊥平面ABCD.
(2)取AD中點O,連結PO,則PO⊥AD,且PO![]() ,
,
由平面PAD⊥平面ABCD,知PO⊥平面ABCD,
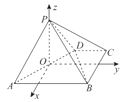
以O為坐標原點,以過點O且平行于BC的直線為x軸,過點O且平行于AB的直線為y軸,
直線PO為z軸,建立如圖所示的空間直角坐標系,
則A(![]() ,0),B(
,0),B(![]() ,0),C(
,0),C(![]() ,0),P(0,0,
,0),P(0,0,![]() ),
),
![]() (﹣1,0,0),
(﹣1,0,0),![]() (
(![]() ,
,![]() ),
),
設平面PBC的法向量![]() (x,y,z),
(x,y,z),
則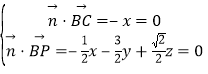 ,取z
,取z![]() ,得
,得![]() (0,
(0,![]() ,
,![]() ),
),
∵![]() (
(![]() ,
,![]() ),
),
∴cos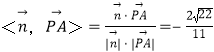 ,
,
∴直線PA與平面PBC所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
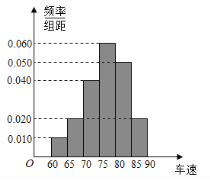
【題目】2012年“雙節”期間,高速公路車輛較多![]() 某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速
某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速![]() 分成六段:
分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后得到如圖的頻率分布直方圖.
后得到如圖的頻率分布直方圖.
![]() 某調查公司在采樣中,用到的是什么抽樣方法?
某調查公司在采樣中,用到的是什么抽樣方法?
![]() 求這40輛小型車輛車速的眾數和中位數的估計值.
求這40輛小型車輛車速的眾數和中位數的估計值.
![]() 若從車速在
若從車速在![]() 的車輛中任抽取2輛,求車速在
的車輛中任抽取2輛,求車速在![]() 的車輛至少有一輛的概率.
的車輛至少有一輛的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為了解中學生的課外閱讀時間,決定在該中學的1200名男生和800名女生中按分層抽樣的方法抽取20名學生,對他們的課外閱讀時間進行問卷調查。現在按課外閱讀時間的情況將學生分成三類:A類(不參加課外閱讀),B類(參加課外閱讀,但平均每周參加課外閱讀的時間不超過3小時),C類(參加課外閱讀,且平均每周參加課外閱讀的時間超過3小時)。調查結果如下表:
A類 | B類 | C類 | |
男生 | x | 5 | 3 |
女生 | y | 3 | 3 |
(1)求出表中x,y的值;
(2)根據表中的統計數據,完成下面的列聯表,并判斷是否有90%的把握認為“參加課外閱讀與否”與性別有關;
男生 | 女生 | 總計 | |
不參加課外閱讀 | |||
參加課外閱讀 | |||
總計 |
附:K2=![]()
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,過點
,過點![]() 向圓
向圓![]() 引兩條切線
引兩條切線![]() ,
,![]() ,切點為
,切點為![]() ,
,![]() ,若點
,若點![]() 的坐標為
的坐標為![]() ,則直線
,則直線![]() 的方程為____________;若
的方程為____________;若![]() 為直線
為直線![]() 上一動點,則直線
上一動點,則直線![]() 經過定點__________.
經過定點__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】求滿足下列條件的橢圓的標準方程:
(1)焦點在y軸上,焦距是4,且經過點M(3,2);
(2)c∶a=5∶13,且橢圓上一點到兩焦點的距離的和為26.
查看答案和解析>>
科目:高中數學 來源: 題型:
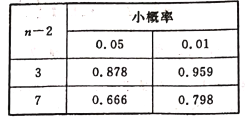
【題目】隨著電子閱讀的普及,傳統紙質媒體遭受到了強烈的沖擊.某雜志社近9年來的紙質廣告收入如下表所示:

根據這9年的數據,對![]() 和
和![]() 作線性相關性檢驗,求得樣本相關系數的絕對值為0.243;
作線性相關性檢驗,求得樣本相關系數的絕對值為0.243;
根據后5年的數據,對![]() 和
和![]() 作線性相關性檢驗,求得樣本相關系數的絕對值為0.984.
作線性相關性檢驗,求得樣本相關系數的絕對值為0.984.
(1)如果要用線性回歸方程預測該雜志社2019年的紙質廣告收入,現在有兩個方案,
方案一:選取這9年數據進行預測,方案二:選取后5年數據進行預測.
從實際生活背景以及線性相關性檢驗的角度分析,你覺得哪個方案更合適?
附:相關性檢驗的臨界值表:
(2)某購物網站同時銷售某本暢銷書籍的紙質版本和電子書,據統計,在該網站購買該書籍的大量讀者中,只購買電子書的讀者比例為![]() ,紙質版本和電子書同時購買的讀者比例為
,紙質版本和電子書同時購買的讀者比例為![]() ,現用此統計結果作為概率,若從上述讀者中隨機調查了3位,求購買電子書人數多于只購買紙質版本人數的概率.
,現用此統計結果作為概率,若從上述讀者中隨機調查了3位,求購買電子書人數多于只購買紙質版本人數的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面命題正確的是( )
A.“![]() ”是“
”是“![]() ”的 充 分不 必 要條件
”的 充 分不 必 要條件
B.命題“若![]() ,則
,則![]() ”的 否 定 是“ 存 在
”的 否 定 是“ 存 在![]() ,則
,則![]() ”.
”.
C.設![]() ,則“
,則“![]() 且
且![]() ”是“
”是“![]() ”的必要而不充分條件
”的必要而不充分條件
D.設![]() ,則“
,則“![]() ”是“
”是“![]() ”的必要 不 充 分 條件
”的必要 不 充 分 條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為定義域R上的奇函數,且在R上是單調遞增函數,函數
為定義域R上的奇函數,且在R上是單調遞增函數,函數![]() ,數列
,數列![]() 為等差數列,且公差不為0,若
為等差數列,且公差不為0,若![]() ,則
,則![]() ( )
( )
A. 45B. 15C. 10D. 0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com