
【題目】如圖所示的多面體的底面![]() 為直角梯形,四邊形
為直角梯形,四邊形![]() 為矩形,且
為矩形,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 的中點.
的中點.
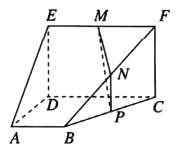
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)答案見解析.(2)![]()
【解析】
(1)先證明![]() 平面
平面![]() ,可得
,可得![]() ,取
,取![]() 中點
中點![]() ,利用等腰三角形的性質(zhì)可得
,利用等腰三角形的性質(zhì)可得![]() ,由線面垂直的判定即可得證;
,由線面垂直的判定即可得證;
(2)建立空間直角坐標系,求出各點坐標后,再求出平面![]() 的一個法向量
的一個法向量![]() 和直線
和直線![]() 的方向向量
的方向向量![]() ,求出兩向量夾角的余弦值后利用平方關(guān)系即可得解.
,求出兩向量夾角的余弦值后利用平方關(guān)系即可得解.
(1)證明:![]()
![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,![]()
![]() ,
,
![]() 四邊形
四邊形![]() 為矩形,
為矩形,![]()
![]() ,
,
又![]()
![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() ,
,
取![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,
![]() 點
點![]() ,
,![]() ,
,![]() ,
,![]() 同在平面
同在平面![]() 內(nèi).
內(nèi).
在![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 中點,
中點,
![]()
![]() ,
,
又![]()
![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() .
.
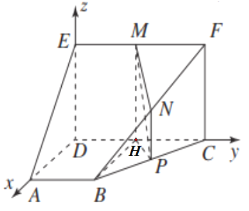
(2)由(1)知![]() ,
,![]() ,
,![]() 三條直線兩兩垂直且交于點
三條直線兩兩垂直且交于點![]() ,以
,以![]() 為原點,
為原點,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標系,如圖.
軸,建立空間直角坐標系,如圖.
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() 分別為
分別為![]() ,
,![]() 中點,可得
中點,可得![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,
設(shè)平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則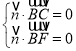 ,即
,即![]() ,
,
令![]() ,可得
,可得![]() ,
,![]() ,
,![]()
![]() ,
,
所以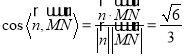 .
.
所以![]() 與平面
與平面![]() 所成角的余弦值為
所成角的余弦值為 .
.


科目:高中數(shù)學 來源: 題型:
【題目】電影《厲害了,我的國》于2018年3月正式登陸全國院線,網(wǎng)友紛紛表示,看完電影熱血沸騰“我為我的國家驕傲,我為我是中國人驕傲!”《厲害了,我的國》正在召喚我們每一個人,不忘初心,用奮斗書寫無悔人生,小明想約甲、乙、丙、丁四位好朋友一同去看《厲害了,我的國》,并把標識為![]() 的四張電影票放在編號分別為1,2,3,4的四個不同的盒子里,讓四位好朋友進行猜測:
的四張電影票放在編號分別為1,2,3,4的四個不同的盒子里,讓四位好朋友進行猜測:
甲說:第1個盒子里放的是![]() ,第3個盒子里放的是
,第3個盒子里放的是![]()
乙說:第2個盒子里放的是![]() ,第3個盒子里放的是
,第3個盒子里放的是![]()
丙說:第4個盒子里放的是![]() ,第2個盒子里放的是
,第2個盒子里放的是![]()
丁說:第4個盒子里放的是![]() ,第3個盒子里放的是
,第3個盒子里放的是![]()
小明說:“四位朋友你們都只說對了一半”
可以預(yù)測,第4個盒子里放的電影票為_________
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】改革開放以來,中國快遞行業(yè)持續(xù)快速發(fā)展,快遞業(yè)務(wù)量從上世紀![]() 年代的
年代的![]() 萬件提升到2018年的
萬件提升到2018年的![]() 億件,快遞行業(yè)的發(fā)展也給我們的生活帶來了很大便利.已知某市某快遞點的收費標準為:首重(重量小于等于
億件,快遞行業(yè)的發(fā)展也給我們的生活帶來了很大便利.已知某市某快遞點的收費標準為:首重(重量小于等于![]() )收費
)收費![]() 元,續(xù)重
元,續(xù)重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一個包裹重量為
算). (如:一個包裹重量為![]() 則需支付首付
則需支付首付![]() 元,續(xù)重
元,續(xù)重![]() 元,一共
元,一共![]() 元快遞費用)
元快遞費用)
(1)若你有三件禮物![]() 重量分別為
重量分別為![]() ,要將三個禮物分成兩個包裹寄出(如:
,要將三個禮物分成兩個包裹寄出(如:![]() 合為一個包裹,
合為一個包裹,![]() 一個包裹),那么如何分配禮物,使得你花費的快遞費最少?
一個包裹),那么如何分配禮物,使得你花費的快遞費最少?
(2)為了解該快遞點2019年的攬件情況,在2019年內(nèi)隨機抽查了![]() 天的日攬收包裹數(shù)(單位:件),得到如下表格:
天的日攬收包裹數(shù)(單位:件),得到如下表格:
包裹數(shù)(單位:件) |
|
|
|
|
天數(shù)(天) |
|
|
|
|
現(xiàn)用這![]() 天的日攬收包裹數(shù)估計該快遞點2019年的日攬收包裏數(shù).若從2019年任取
天的日攬收包裹數(shù)估計該快遞點2019年的日攬收包裏數(shù).若從2019年任取![]() 天,記這
天,記這![]() 天中日攬收包裹數(shù)超過
天中日攬收包裹數(shù)超過![]() 件的天數(shù)為隨機變量
件的天數(shù)為隨機變量![]() 求
求![]() 的分布列和期望
的分布列和期望
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).以坐標原點為極點,
為參數(shù)).以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的方程為
的方程為![]() .
.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)射線![]() 與曲線
與曲線![]() 、直線
、直線![]() 分別交于
分別交于![]() 、
、![]() 兩點(
兩點(![]() 異于極點
異于極點![]() ),求
),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
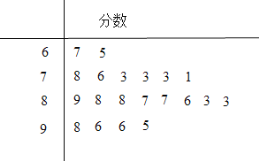
【題目】某大型單位舉行了一次全體員工都參加的考試,從中隨機抽取了20人的分數(shù).以下莖葉圖記錄了他們的考試分數(shù)(以十位數(shù)字為莖,個位數(shù)字為葉):若分數(shù)不低于95分,則稱該員工的成績?yōu)椤皟?yōu)秀”.

組別 | 分組 | 頻數(shù) | 頻率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
(Ⅰ)從這20人中成績?yōu)椤皟?yōu)秀”的員工中任取2人,求恰有1人的分數(shù)為96的概率;
(Ⅱ)根據(jù)這20人的分數(shù)補全頻率分布表和頻率分布直方圖,并根據(jù)頻率分布直方圖估計所有員工的平均分數(shù)(同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,矩形![]() 所在的平面與正三角形
所在的平面與正三角形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() 為
為![]() 的中點,連接
的中點,連接![]() .
.
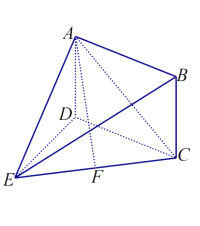
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】近年來,隨著互聯(lián)網(wǎng)的發(fā)展,諸如“滴滴打車”“神州專車”等網(wǎng)約車服務(wù)在我國各:城市迅猛發(fā)展,為人們出行提供了便利,但也給城市交通管理帶來了一些困難.為掌握網(wǎng)約車在![]() 省的發(fā)展情況,
省的發(fā)展情況,![]() 省某調(diào)查機構(gòu)從該省抽取了
省某調(diào)查機構(gòu)從該省抽取了![]() 個城市,分別收集和分析了網(wǎng)約車的
個城市,分別收集和分析了網(wǎng)約車的![]() 兩項指標數(shù)
兩項指標數(shù)![]() ,數(shù)據(jù)如下表所示:
,數(shù)據(jù)如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
|
|
|
|
|
|
|
|
|
|
|
|
經(jīng)計算得: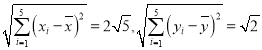
(1)試求![]() 與
與![]() 間的相關(guān)系數(shù)
間的相關(guān)系數(shù)![]() ,并利用
,并利用![]() 說明
說明![]() 與
與![]() 是否具有較強的線性相關(guān)關(guān)系(若
是否具有較強的線性相關(guān)關(guān)系(若![]() ,則線性相關(guān)程度很高,可用線性回歸模型擬合);
,則線性相關(guān)程度很高,可用線性回歸模型擬合);
(2)立![]() 關(guān)于
關(guān)于![]() 的回歸方程,并預(yù)測當
的回歸方程,并預(yù)測當![]() 指標數(shù)為
指標數(shù)為![]() 時,
時,![]() 指標數(shù)的估計值.
指標數(shù)的估計值.
附:相關(guān)公式: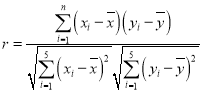 ,
,
參考數(shù)據(jù):![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標原點為極點,
為參數(shù)),以坐標原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,直線
軸的正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)若射線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() ).設(shè)
).設(shè)![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() ,求
,求![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com