Question

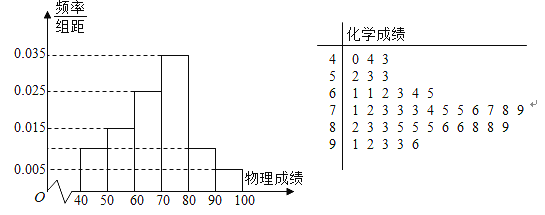
【題目】近年來，在新高考改革中，打破文理分科的“”模式初露端倪，其中語、數、外三門課為必考科目，剩下三門為選考科目選考科目成績采用“賦分制”，即原始分數不直接用，而是按照學生分數在本科目考試的排名來劃分等級并以此打分得到最后得分，假定省規定：選考科目按考生成績從高到低排列，按照占總體、、、分別賦分分、分、分、分，為了讓學生們體驗“賦分制”計算成績的方法，省某高中高一（）班（共人）舉行了以此摸底考試（選考科目全考，單料全班排名），知這次摸底考試中的物理成績（滿分分）頻率分布直方圖，化學成績（滿分分）莖葉圖如圖所示，小明同學在這次考試中物理分，化學多分．

（1）采用賦分制后，求小明物理成績的最后得分；

（2）若小明的化學成績最后得分為分，求小明的原始成績的可能值；

（3）若小明必選物理，其他兩科從化學、生物、歷史、地理、政治五科中任選，求小明此次考試選考科目包括化學的概率．

Answer 1

【答案】（1）分；（2）；（3）.

【解析】

（1）根據物理分判斷所處的百分比，根據百分比確定分數；（2）先排除賦分分的分數，然后利用百分比計算賦分分的人數，結合數據，給出可能的取值；（3）采用列舉法以及古典概型的概率計算公式來求解.

（1）∵，，

∴此次考試物理成績落在，內的頻率依次為，，頻率之和為，且小明的物理成績為分，大于分，處于前，

∴小明物理成績的最后得分為分.

（2）因為名學生中，賦分分的有人，這六人成績分別為，，，，，；賦分分的有人，其中包含多分的共人，多分的有人，分數分別為，，，；因為小明的化學成績最后得分為分，且小明化學多分，所以小明的原始成績的可能值為，，，.

（3）記物理、化學、生物、歷史、地理、政治依次為，，，，，，小明的所有可能選法有，，，，，

，，，，共10種，

其中包括化學的有，，，共4種，

∵若小明必選物理，其他兩科在剩下的五科中任選，所選科目包括化學的概率為：.