【題目】某市10000名職業中學高三學生參加了一項綜合技能測試，從中隨機抽取100名學生的測試成績，制作了以下的測試成績
（滿分是184分）的頻率分布直方圖.
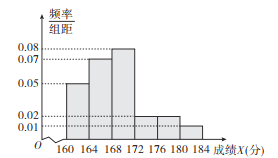
市教育局規定每個學生需要繳考試費100元.某企業根據這100000名職業中學高三學生綜合技能測試成績來招聘員工，劃定的招聘錄取分數線為172分，且補助已經被錄取的學生每個人
元的交通和餐補費.
（1）已知甲、乙兩名學生的測試成績分別為168分和170分，求技能測試成績的中位數，并對甲、乙的成績作出客觀的評價；
（2）令
表示每個學生的交費或獲得交通和餐補費的代數和，把用的函數來表示，并根據頻率分布直方圖估計
的概率.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】如圖，在四棱柱ABCDA1B1C1D1中，側棱A1A⊥底面ABCD，AB⊥AC，AB＝1，AC＝AA1＝2，AD＝CD＝
，且點M和N分別為B1C和D1D的中點．
（Ⅰ）求證：MN∥平面ABCD；
（Ⅱ）求二面角D1－AC－B1的正弦值；
（Ⅲ）設E為棱A1B1上的點．若直線NE和平面ABCD所成角的正弦值為
，求線段A1E的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，其圖像相鄰的兩個對稱中心之間的距離為
，且有一條對稱軸為直線
，則下列判斷正確的是 （ ）
A. 函數
的最小正周期為
B. 函數的圖象關于直線
對稱
C. 函數在區間
上單調遞增
D. 函數的圖像關于點
對稱
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知以點
為圓心的圓C被直線
截得的弦長為
．
（1）求圓C的標準方程：
（2）求過
與圓C相切的直線方程：
（3）若Q是直線
上的動點，QR，QS分別切圓C于R，S兩點．試問：直線RS是否恒過定點？若是，求出恒過點坐標：若不是，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，若在定義域內存在
，使得
成立，則稱為函數
的局部對稱點.
（1）若
，證明：函數
必有局部對稱點；
（2）若函數
在區間
內有局部對稱點，求實數
的取值范圍；
（3）若函數
在
上有局部對稱點，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，其圖象與
軸相鄰的兩個交點的距離為
.
（1）求函數
的解析式；
（2）若將的圖象向左平移
個長度單位得到函數
的圖象恰好經過點
，求當
取得最小值時，在
上的單調區間.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高三年級有500名學生，為了了解數學學科的學習情況，現隨機抽出若干名學生在一次測試中的數學成績（滿分150分），制成如下頻率分布表：
分組 | 頻數 | 頻率 |
| ① | ② |
| 0.050 | |
| 0.200 | |
| 12 | 0.300 |
| 0.275 | |
| 4 | ③ |
| 0.050 | |
合計 | ④ |
（1）①②③④處應分別填什么？
（2）根據頻率分布表完成頻率分布直方圖.
（3）試估計該校高三年級在這次測試中數學成績的平均分.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知以點
為圓心的圓過點
和
，線段
的垂直平分線交圓于點
，且
.
（1）求直線
的方程；
（2）求圓的方程；
（3）是否存在點
在圓上，使得
的面積為
？若存在，請指出共有幾個這樣的點？說明理由，并求出這些點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
