
【題目】已知以點![]() 為圓心的圓C被直線
為圓心的圓C被直線![]() 截得的弦長為
截得的弦長為![]() .
.
(1)求圓C的標準方程:
(2)求過![]() 與圓C相切的直線方程:
與圓C相切的直線方程:
(3)若Q是直線![]() 上的動點,QR,QS分別切圓C于R,S兩點.試問:直線RS是否恒過定點?若是,求出恒過點坐標:若不是,說明理由.
上的動點,QR,QS分別切圓C于R,S兩點.試問:直線RS是否恒過定點?若是,求出恒過點坐標:若不是,說明理由.
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)直線RS恒過定點
(3)直線RS恒過定點![]()
【解析】
(1)由弦長可得![]() ,進而求解即可;
,進而求解即可;
(2)分別討論直線的斜率存在與不存在的情況,再利用圓心到直線距離等于半徑求解即可;
(3)由QR,QS分別切圓C于R,S兩點,可知![]() ,
,![]() 在以
在以![]() 為直徑的圓上,設
為直徑的圓上,設![]() 為
為![]() ,則可得到以
,則可得到以![]() 為直徑的圓的方程,與圓
為直徑的圓的方程,與圓![]() 聯立可得
聯立可得![]() ,由
,由![]() 求解即可
求解即可
(1)由題,設點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
則![]() ,
,
則弦長![]() ,解得
,解得![]() ,
,
所以圓![]() 的標準方程為:
的標準方程為:![]()
(2)當切線斜率不存在時,直線方程為![]() ,圓心到直線距離為2,故此時相切;
,圓心到直線距離為2,故此時相切;
當切線斜率存在時,設切線方程為![]() ,即
,即![]() ,
,
則 ,解得
,解得![]() ,
,
則直線方程為![]() ,即
,即![]() ,
,
綜上,切線方程為![]() 或
或![]()
(3)直線RS恒過定點,
由題,![]() ,則
,則![]() ,
,![]() 在以
在以![]() 為直徑的圓上,
為直徑的圓上,
設![]() 為
為![]() ,
,
則以![]() 為直徑的圓的方程為:
為直徑的圓的方程為: ,
,
整理可得![]() ,
,
與圓![]() :
:![]() 聯立可得:
聯立可得:![]() ,
,
即![]() ,
,
令![]() ,解得
,解得 ,
,
故無論![]() 取何值時,直線
取何值時,直線![]() 恒過定點
恒過定點![]()


科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 某廠一批產品的次品率為![]() ,則任意抽取其中10件產品一定會發現一件次品
,則任意抽取其中10件產品一定會發現一件次品
B. 擲一枚硬幣,連續出現5次正面向上,第六次出現反面向上的概率與正面向上的概率仍然都為0.5
C. 某醫院治療一種疾病的治愈率為10%,那么前9個病人都沒有治愈,第10個人就一定能治愈
D. 氣象部門預報明天下雨的概率是90%,說明明天該地區90%的地方要下雨,其余10%的地方不會下雨
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線C1的漸近線是![]() x±2y=0,焦點坐標是F1(-
x±2y=0,焦點坐標是F1(-![]() ,0)、F2(
,0)、F2(![]() ,0).
,0).
(1)求雙曲線C1的方程;
(2)若橢圓C2與雙曲線C1有公共的焦點,且它們的離心率之和為![]() ,點P在橢圓C2上,且|PF1|=4,求∠F1PF2的大小.
,點P在橢圓C2上,且|PF1|=4,求∠F1PF2的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區間是:[50,60),[60,70),[70,80),[80,90),[90,100].
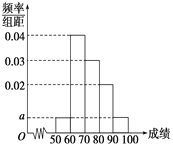
(1)求圖中a的值;
(2)根據頻率分布直方圖,估計這100名學生語文成績的平均分;
(3)若這100名學生語文成績某些分數段的人數(x)與數學成績相應分數段的人數(y)之比如下表所示,求數學成績在[50,90)之外的人數.
分數段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 是亞太區域國家與地區加強多邊經濟聯系、交流與合作的重要組織,其宗旨和目標是“相互依存、共同利益,堅持開放性多邊貿易體制和減少區域間貿易壁壘.”2017年
是亞太區域國家與地區加強多邊經濟聯系、交流與合作的重要組織,其宗旨和目標是“相互依存、共同利益,堅持開放性多邊貿易體制和減少區域間貿易壁壘.”2017年![]() 會議于11月10日至11日在越南峴港舉行.某研究機構為了了解各年齡層對
會議于11月10日至11日在越南峴港舉行.某研究機構為了了解各年齡層對![]() 會議的關注程度,隨機選取了100名年齡在
會議的關注程度,隨機選取了100名年齡在![]() 內的市民進行了調查,并將結果繪制成如圖所示的頻率分布直方圖(分組區間分別為
內的市民進行了調查,并將結果繪制成如圖所示的頻率分布直方圖(分組區間分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
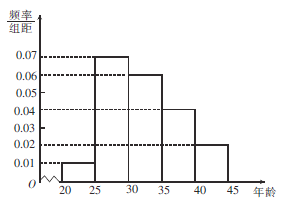
(1)求選取的市民年齡在![]() 內的人數;
內的人數;
(2)若從第3,4組用分層抽樣的方法選取5名市民進行座談,再從中選取2人參與![]() 會議的宣傳活動,求參與宣傳活動的市民中至少有一人的年齡在
會議的宣傳活動,求參與宣傳活動的市民中至少有一人的年齡在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市10000名職業中學高三學生參加了一項綜合技能測試,從中隨機抽取100名學生的測試成績,制作了以下的測試成績![]() (滿分是184分)的頻率分布直方圖.
(滿分是184分)的頻率分布直方圖.
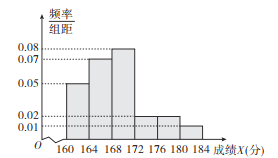
市教育局規定每個學生需要繳考試費100元.某企業根據這100000名職業中學高三學生綜合技能測試成績來招聘員工,劃定的招聘錄取分數線為172分,且補助已經被錄取的學生每個人![]() 元的交通和餐補費.
元的交通和餐補費.
(1)已知甲、乙兩名學生的測試成績分別為168分和170分,求技能測試成績![]() 的中位數,并對甲、乙的成績作出客觀的評價;
的中位數,并對甲、乙的成績作出客觀的評價;
(2)令![]() 表示每個學生的交費或獲得交通和餐補費的代數和,把
表示每個學生的交費或獲得交通和餐補費的代數和,把![]() 用
用![]() 的函數來表示,并根據頻率分布直方圖估計
的函數來表示,并根據頻率分布直方圖估計![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() =(
=(![]() sin x,cos x),
sin x,cos x),![]() =(cos x,cos x),
=(cos x,cos x),![]() =(2
=(2![]() ,1).
,1).
(1)若![]() ∥
∥![]() ,求sin xcos x的值;
,求sin xcos x的值;
(2)若0<x≤![]() ,求函數f(x)=
,求函數f(x)=![]() ·
·![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() (
(![]() ),
),![]() .
.
(1)若曲線![]() 與
與![]() 在它們的交點
在它們的交點![]() 處有相同的切線,求實數
處有相同的切線,求實數![]() ,
,![]() 的值;
的值;
(2)當![]() 時,若函數
時,若函數![]() 在區間
在區間![]() 內恰有兩個零點,求實數a的取值范圍;
內恰有兩個零點,求實數a的取值范圍;
(3)當![]() ,
,![]() 時,求函數
時,求函數![]() 在區間
在區間![]() 上的最小值.
上的最小值.
[選修4-4:坐標系與參數方程]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高中為了選拔學生參加“全國高中數學聯賽”,先在本校進行初賽(滿分150分),隨機抽取100名學生的成績作為樣本,并根據他們的初賽成績得到如圖所示的頻率分布直方圖.

(1)求頻率分布直方圖中a的值;
(2)根據頻率分布直方圖,估計這次初賽成績的平均數、中位數、眾數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com