
【題目】如圖,正方形![]() 和梯形
和梯形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,
,![]() ,
,![]() 分別為線段
分別為線段![]() ,
,![]() 的中點.
的中點.

(Ⅰ)求證:![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,求證:平面
,求證:平面![]() 平面
平面![]() .
.
【答案】詳見解析
【解析】
(Ⅰ)推導出AC⊥BD,從而AC⊥平面BDEF,由此能證明AC⊥BF;
(Ⅱ)法一:取AD中點M,連接ME,MG,則GM∥BD且![]() ,從而GM∥EF且GM=EF,進而四邊形GMEF為平行四邊形,從而GF∥ME,由此能證明GF∥平面ADE;
,從而GM∥EF且GM=EF,進而四邊形GMEF為平行四邊形,從而GF∥ME,由此能證明GF∥平面ADE;
法二:連接OF,OG,推導出四邊形DOFE為平行四邊形,從而OF∥DE,進而OF∥平面ADE,由O,G分別為BD,AB的中點,得OG∥AD,從而OG∥平面ADE,進而平面GOF∥平面ADE,由此能證明GF∥平面ADE;
(Ⅲ)連接OH,則OH∥DF,由DF⊥BF,得OH⊥BF,再由BF⊥AC,得BF⊥平面AHC,由此能證明平面AHC⊥平面BGF.
解:(Ⅰ)因為![]() 為正方形,所以
為正方形,所以![]() .又因為平面
.又因為平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .又因為
.又因為![]() 平面
平面![]() ,
,
所以![]() .
.
(Ⅱ)方法一:取![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,
,
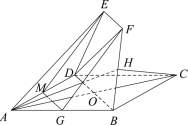
在![]() 中,
中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,
所以![]() 且
且![]() .又因為
.又因為![]() 且
且![]() ,
,
所以![]() 且
且![]() .所以四邊形
.所以四邊形![]() 為平行四邊形.
為平行四邊形.
所以![]() .因為
.因為![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
方法二:連接![]() ,
,![]() ,
,
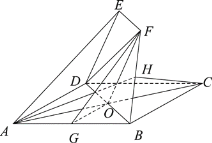
因為![]() 且
且![]() ,
,
所以![]() 且
且![]() .
.
所以四邊形![]() 為平行四邊形.所以
為平行四邊形.所以![]() .
.
因為![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .因為
.因為![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,
所以![]() .又因為
.又因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .因為
.因為![]() ,
,
所以平面![]() 平面
平面![]() .因為
.因為![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅲ)連接![]() ,
,
在![]() 中,
中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,
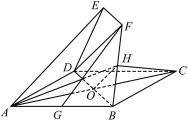
所以![]() .因為
.因為![]() ,
,
所以![]() .因為
.因為![]() ,
,
![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .因為
.因為![]() 平面
平面![]() ,
,
所以平面![]()
![]() 平面
平面![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的兩個焦點與短軸的一個端點是直角三角形的三個頂點,直線
的兩個焦點與短軸的一個端點是直角三角形的三個頂點,直線![]() :
: ![]() 與橢圓
與橢圓![]() 有且只有一個公共點.
有且只有一個公共點.
(Ⅰ)求橢圓![]() 的方程及點
的方程及點![]() 的坐標;
的坐標;
(Ⅱ)設![]() 是坐標原點,直線
是坐標原點,直線![]() 平行于
平行于![]() ,與橢圓
,與橢圓![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() ,且與直線
,且與直線![]() 交于點
交于點![]() ,證明:存在常數
,證明:存在常數![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】部分與整體以某種相似的方式呈現稱為分形,一個數學意義上分形的生成是基于一個不斷迭代的方程式,即一種基于遞歸的反饋系統.分形幾何學不僅讓人們感悟到科學與藝木的融合,數學與藝術審美的統一,而且還有其深刻的科學方法論意義.如圖,由波蘭數學家謝爾賓斯基1915年提出的謝爾賓斯基三角形就屬于-種分形,具體作法是取一個實心三角形,沿三角形的三邊中點連線,將它分成4個小三角形,去掉中間的那一個小三角形后,對其余3個小三角形重復上述過程逐次得到各個圖形.

若在圖④中隨機選取-點,則此點取自陰影部分的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,則“存在常數
,則“存在常數![]() ,對任意的
,對任意的![]() ,且
,且![]() ,都有
,都有![]() ”是“數列
”是“數列![]() 為等差數列”的( )
為等差數列”的( )
A. 充分而不必要條件 B. 必要而不充分條件
C. 充分必要條件 D. 既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年1月22日,依照中國文聯及中國民間文藝家協會命名中國觀音文化之鄉的有關規定,中國文聯、中國民協正式命名四川省遂寧市為“中國觀音文化之鄉”.
下表為2014年至2018年觀音文化故里某土特產企業的線下銷售額(單位:萬元)
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
線下銷售額 | 90 | 170 | 210 | 280 | 340 |
為了解“祝福觀音、永保平安”活動的支持度.某新聞調查組對40位老年市民和40位年輕市民進行了問卷調查(每位市民從“很支持”和“支持”中任選一種),其中很支持的老年市民有30人,支持的年輕市民有15人.
(1)從以上5年中任選2年,求其銷售額均超過200萬元的概率;
(2)請根據以上信息列出列聯表,并判斷能否有85%的把握認為支持程度與年齡有關.
附:![]() ,其中
,其中![]()
參考數據:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com