【題目】選修4-4：坐標系與參數方程
在直角坐標系
中，過點
的直線
的參數方程為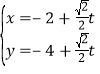
（
為參數），以坐標原點
為極點，以
軸正半軸為極軸，建立極坐標系，已知曲線
的極坐標方程為
，記直線與曲線分別交于
兩點.
（1）求曲線和的直角坐標方程；
（2）證明：
成等比數列.
新非凡教輔沖刺100分系列答案科目：高中數學 來源： 題型：
【題目】已知數列
中
，前
項和為
，若對任意的
，均有
（
是常數，且
）成立，則稱數列為“
數列”.
（1）若數列為“
數列”，求數列的前項和；
（2）若數列為“
數列”，且
為整數，試問：是否存在數列，使得
對一切
，恒成立？如果存在，求出這樣數列的的所有可能值，如果不存在，請說明理由；
（3）若數列為“數列”，且
，證明：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學生將語文、數學、英語、物理、化學、生物6科的作業安排在周六、周日完成，要求每天至少完成兩科，且數學，物理作業不在同一天完成，則完成作業的不同順序種數為（ ）
A. 600B. 812C. 1200D. 1632
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】盒子中裝有四張大小形狀均相同的卡片，卡片上分別標有數
其中
是虛數單位．稱“從盒中隨機抽取一張，記下卡片上的數后并放回”為一次試驗（設每次試驗的結果互不影響）．
（1）求事件
“在一次試驗中，得到的數為虛數”的概率
與事件
“在四次試驗中，
至少有兩次得到虛數” 的概率
；
（2）在兩次試驗中，記兩次得到的數分別為
，求隨機變量
的分布列與數學期望
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】由中央電視臺綜合頻道（
）和唯眾傳媒聯合制作的《開講啦》是中國首檔青年電視公開課，每期節目由一位知名人士講述自己的故事，分享他們對于生活和生命的感悟，給予中國青年現實的討論和心靈的滋養，討論青年們的人生問題，同時也在討論青春中國的社會問題，受到青年觀眾的喜愛，為了了解觀眾對節目的喜愛程度，電視臺隨機調查了A、B兩個地區共100名觀眾，得到如下的
列聯表：
非常滿意 | 滿意 | 合計 | |
A | 30 | y | |
B | x | z | |
合計 |
已知在被調查的100名觀眾中隨機抽取1名，該觀眾是
地區當中“非常滿意”的觀眾的概率為0.35，且
.請完成上述表格，并根據表格判斷是否有95%的把握認為觀眾的滿意程度與所在地區有關系？
附:參考公式：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】當生物死亡后，它機體內原有的碳14會按確定的規律衰減.按照慣例，人們將每克組織的碳14含量作為一個單位大約每經過5730年，一個單位的碳14衰減為原來的一半，這個時間稱為“半衰期”.當死亡生物組織內的碳14的含量不足死亡前的千分之一時，用一般的放射性探測器就測不到碳14了.如果用一般的放射性探測器不能測到碳14，那么死亡生物組織內的碳14至少經過了_____個“半衰期”.（提示：
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方體
的棱長為
， 
分別是
的中點，點
在棱
上， 
（
）.
（Ⅰ）三棱錐
的體積分別為
，當
為何值時， 
最大？最大值為多少？
（Ⅱ）若
平面
，證明：平面
平面
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】圖①是一棟新農村別墅，它由上部屋頂和下部主體兩部分組成．如圖②，屋頂由四坡屋面構成，其中前后兩坡屋面ABFE和CDEF是全等的等腰梯形，左右兩坡屋面EAD和FBC是全等的三角形．點F在平面ABCD和BC上的射影分別為H，M．已知HM 5 m，BC 10 m，梯形ABFE的面積是△FBC面積的2.2倍．設∠FMH 
．
（1）求屋頂面積S關于的函數關系式；
（2）已知上部屋頂造價與屋頂面積成正比，比例系數為k（k為正的常數），下部主體造價與其 高度成正比，比例系數為16 k．現欲造一棟上、下總高度為6 m的別墅，試問：當為何值時，總造價最低？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
