
【題目】紅鈴蟲是棉花的主要害蟲之一,能對農作物造成嚴重傷害,每只紅鈴蟲的平均產卵數y和平均溫度x有關,現收集了以往某地的7組數據,得到下面的散點圖及一些統計量的值.(表中![]() )
)
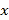
平均溫度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 | ||
平均產卵數 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | ||
|
|
|
|
| |||||
27.429 | 81.286 | 3.612 | 40.182 | 147.714 | |||||
(1)根據散點圖判斷,![]() 與
與![]() (其中
(其中![]() 自然對數的底數)哪一個更適宜作為平均產卵數y關于平均溫度x的回歸方程類型?(給出判斷即可,不必說明理由)并由判斷結果及表中數據,求出y關于x的回歸方程.(計算結果精確到小數點后第三位)
自然對數的底數)哪一個更適宜作為平均產卵數y關于平均溫度x的回歸方程類型?(給出判斷即可,不必說明理由)并由判斷結果及表中數據,求出y關于x的回歸方程.(計算結果精確到小數點后第三位)
(2)根據以往統計,該地每年平均溫度達到28℃以上時紅鈴蟲會造成嚴重傷害,需要人工防治,其他情況均不需要人工防治記該地每年平均溫度達到28℃以上的概率為![]() .
.
①記該地今后5年中,恰好需要3次人工防治的概率為![]() ,求
,求![]() 的最大值,并求出相應的概率p.
的最大值,并求出相應的概率p.
②當![]() 取最大值時,記該地今后5年中,需要人工防治的次數為X,求X的數學期望和方差.
取最大值時,記該地今后5年中,需要人工防治的次數為X,求X的數學期望和方差.
附:線性回歸方程系數公式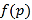 .
.
【答案】(1)![]() 更適宜,
更適宜,![]() ;(2)①
;(2)①![]() ,
,![]() ;②
;②![]() ,
,![]()
【解析】
(1)根據散點圖選擇合適函數模擬,利用變量![]() ,構造線性回歸方程,利用已知量求解出
,構造線性回歸方程,利用已知量求解出![]() 關于
關于![]() 的線性回歸方程,即可求解出y關于x的回歸方程;
的線性回歸方程,即可求解出y關于x的回歸方程;
(2)①先表示出![]() ,然后根據
,然后根據![]() 分析出
分析出![]() 的最大值以及
的最大值以及![]() 的值;
的值;
②根據![]() 的值以及二項分布的均值與方差的計算方法求解出結果即可.
的值以及二項分布的均值與方差的計算方法求解出結果即可.
解:(1)根據散點圖可以判斷,![]() 更適宜作為平均產卵數
更適宜作為平均產卵數
y關于平均溫度x的回歸方程類型;
對![]() 兩邊取自然對數,得
兩邊取自然對數,得![]() ;
;
令![]() ,得
,得![]() ;
;
因為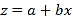 ,
,
![]() ;
;
所以z關于x的回歸方程為![]() ;
;
所以y關于x的回歸方程為![]() ;
;
(2)(i)由![]() ,
,
得![]() ,
,
因為![]() ,令
,令![]() ,得
,得![]() ,解得
,解得![]() ;
;
所以![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
所以![]() 有唯一的極大值為
有唯一的極大值為![]() ,也是最大值;
,也是最大值;
所以當![]() 時,
時,![]() ;
;
(ii)由(i)知,當![]() 取最大值時,
取最大值時,![]() ,所以
,所以![]() ,
,
所以X的數學期望為![]() ,
,
方差為![]() .
.


 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:高中數學 來源: 題型:
【題目】對于定義在![]() 上的函數
上的函數![]() ,若函數
,若函數![]() 滿足:①在區間
滿足:①在區間![]() 上單調遞減;②存在常數p,使其值域為
上單調遞減;②存在常數p,使其值域為![]() ,則稱函數
,則稱函數![]() 為
為![]() 的“漸近函數”;
的“漸近函數”;
(1)證明:函數![]() 是函數
是函數![]()
![]() 的漸近函數,并求此時實數p的值;
的漸近函數,并求此時實數p的值;
(2)若函數![]()
![]()
![]() ,證明:當
,證明:當![]() 時,
時,![]() 不是
不是![]() 的漸近函數.
的漸近函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)![]() a(x﹣1)2+(x﹣2)ex(a>0).
a(x﹣1)2+(x﹣2)ex(a>0).
(1)討論函數f(x)的單調性;
(2)若關于x的方程f(x)![]() a=0存在3個不相等的實數根,求實數a的取值范圍.
a=0存在3個不相等的實數根,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系xOy的原點為極坐標系的極點,x軸的正半軸為極軸.已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,P是
,P是![]() 上一動點,
上一動點,![]() ,Q的軌跡為
,Q的軌跡為![]() .
.
(1)求曲線![]() 的極坐標方程,并化為直角坐標方程,
的極坐標方程,并化為直角坐標方程,
(2)若點![]() ,直線l的參數方程為
,直線l的參數方程為![]() (t為參數),直線l與曲線
(t為參數),直線l與曲線![]() 的交點為A,B,當
的交點為A,B,當![]() 取最小值時,求直線l的普通方程.
取最小值時,求直線l的普通方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業打算處理一批產品,這些產品每箱100件,以箱為單位銷售.已知這批產品中每箱出現的廢品率只有![]() 或者
或者![]() 兩種可能,兩種可能對應的概率均為0.5.假設該產品正品每件市場價格為100元,廢品不值錢.現處理價格為每箱8400元,遇到廢品不予更換.以一箱產品中正品的價格期望值作為決策依據.
兩種可能,兩種可能對應的概率均為0.5.假設該產品正品每件市場價格為100元,廢品不值錢.現處理價格為每箱8400元,遇到廢品不予更換.以一箱產品中正品的價格期望值作為決策依據.
(1)在不開箱檢驗的情況下,判斷是否可以購買;
(2)現允許開箱,有放回地隨機從一箱中抽取2件產品進行檢驗.
①若此箱出現的廢品率為![]() ,記抽到的廢品數為
,記抽到的廢品數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
②若已發現在抽取檢驗的2件產品中,其中恰有一件是廢品,判斷是否可以購買.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,短軸的兩個端點分別為
,短軸的兩個端點分別為![]() .
.
(Ⅰ)若![]() 為等邊三角形,求橢圓
為等邊三角形,求橢圓![]() 的方程;
的方程;
(Ⅱ)若橢圓![]() 的短軸長為
的短軸長為![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為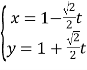 (
(![]() 為參數),以坐標原點為極點,以
為參數),以坐標原點為極點,以![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 交于
交于![]() 兩點,點
兩點,點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() :
: ![]() 滿足:
滿足: ![]() ,
, ![]() 或1(
或1(![]() ).對任意
).對任意![]() ,都存在
,都存在![]() ,使得
,使得![]() .,其中
.,其中![]()
![]() 且兩兩不相等.
且兩兩不相等.
(I)若![]() .寫出下列三個數列中所有符合題目條件的數列的序號;
.寫出下列三個數列中所有符合題目條件的數列的序號;
①1,1,1,2,2,2;②1,1,1,1,2,2,2,2;③1,l,1,1,1,2,2,2,2
(Ⅱ)記![]() .若
.若![]() ,證明:
,證明: ![]() ;
;
(Ⅲ)若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com