
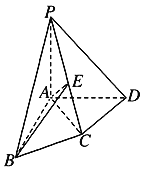
【題目】如圖,在四棱錐![]() 中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中點.證明:
中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中點.證明:
(1)CD⊥AE;
(2)PD⊥平面ABE.
【答案】(1)詳見解析;(2)詳見解析.
【解析】
(1)關鍵證明CD⊥平面PAC,(2)關鍵證明AE⊥PD,AB⊥PD。
證明:(1)在四棱錐![]() 中,
中,
∵PA⊥平面ABCD,CD平面ABCD,
∴PA⊥CD.∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.
而AE平面PAC,∴CD⊥AE.
(2)由PA=AB=BC,∠ABC=60°,可得AC=PA.
∵E是PC的中點,∴AE⊥PC.
由(1)知AE⊥CD,且PC∩CD=C,
∴AE⊥平面PCD.
而PD平面PCD,∴AE⊥PD.
∵PA⊥平面ABCD,∴PA⊥AB.
又∵AB⊥AD且PA∩AD=A,
∴AB⊥平面PAD,而PD平面PAD,
∴AB⊥PD.
又∵AB∩AE=A,
∴PD⊥平面ABE.


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】某超市為調查會員某年度上半年的消費情況制作了有獎調查問卷發放給所有會員,并從參與調查的會員中隨機抽取![]() 名了解情況并給予物質獎勵.調查發現抽取的
名了解情況并給予物質獎勵.調查發現抽取的![]() 名會員消費金額(單位:萬元)都在區間
名會員消費金額(單位:萬元)都在區間![]() 內,調查結果按消費金額分成
內,調查結果按消費金額分成![]() 組,制作成如下的頻率分布直方圖.
組,制作成如下的頻率分布直方圖.
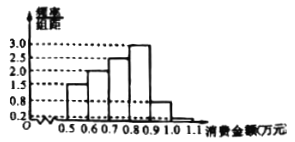
(1)求該![]() 名會員上半年消費金額的平均值與中位數;(以各區間的中點值代表該區間的均值)
名會員上半年消費金額的平均值與中位數;(以各區間的中點值代表該區間的均值)
(2)現采用分層抽樣的方式從前![]() 組中選取
組中選取![]() 人進行消費愛好調查,然后再從前
人進行消費愛好調查,然后再從前![]() 組選取的人中隨機選
組選取的人中隨機選![]() 人,求這
人,求這![]() 人都來自第
人都來自第![]() 組的概率.
組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2021年開始,我省將試行“3+1+2“的普通高考新模式,即除語文、數學、外語3門必選科目外,考生再從物理、歷史中選1門,從化學、生物、地理、政治中選2門作為選考科目.為了幫助學生合理選科,某中學將高一每個學生的六門科目綜合成績按比例均縮放成5分制,繪制成雷達圖.甲同學的成績雷達圖如圖所示,下面敘述一定不正確的是( )

A.甲的物理成績領先年級平均分最多
B.甲有2個科目的成績低于年級平均分
C.甲的成績從高到低的前3個科目依次是地理、化學、歷史
D.對甲而言,物理、化學、地理是比較理想的一種選科結果
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 中心在坐標原點,焦點在
中心在坐標原點,焦點在![]() 軸上,且過
軸上,且過![]() ,直線
,直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點(
兩點(![]() ,
,![]() 兩點不是左右頂點),若直線
兩點不是左右頂點),若直線![]() 的斜率為
的斜率為![]() 時,弦
時,弦![]() 的中點
的中點![]() 在直線
在直線![]() 上.
上.
(Ⅰ)求橢圓![]() 的方程.
的方程.
(Ⅱ)若以![]() ,
,![]() 兩點為直徑的圓過橢圓的右頂點,則直線
兩點為直徑的圓過橢圓的右頂點,則直線![]() 是否經過定點,若是,求出定點坐標,若不是,請說明理由.
是否經過定點,若是,求出定點坐標,若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com