
【題目】已知橢圓C:![]() +
+![]() =1(a>b>0)的一個焦點是F(1,0),且離心率為
=1(a>b>0)的一個焦點是F(1,0),且離心率為![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)設經過點F的直線交橢圓C于M,N兩點,線段MN的垂直平分線交y軸于點P(0,y0),求y0的取值范圍.
【答案】(1)![]() +
+![]() =1. (2)
=1. (2)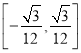
【解析】
試題解:(Ⅰ)設橢圓C的半焦距是c.依題意,得c=1.
因為橢圓C的離心率為![]() ,
,
所以a=2c=2,b2=a2-c2=3.
故橢圓C的方程為![]() +
+![]() =1.
=1.
(Ⅱ)當MN⊥x軸時,顯然y0=0.
當MN與x軸不垂直時,可設直線MN的方程為
y=k(x-1)(k≠0).
由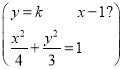
消去y并整理得(3+4k2)x2-8k2x+4(k2-3)=0.
設M(x1,y1),N(x2,y2),線段MN的中點為Q(x3,y3),
則x1+x2=![]() .
.
所以x3=![]() =
=![]() ,y3=k(x3-1)=
,y3=k(x3-1)=![]() .
.
線段MN的垂直平分線的方程為
y+![]() =-
=-![]()
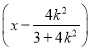 .
.
在上述方程中,令x=0,得y0=![]() =
=![]() .
.
當k<0時,![]() +4k≤-4
+4k≤-4![]() ;當k>0時,
;當k>0時,![]() +4k≥4
+4k≥4![]() .
.
所以-![]() ≤y0<0或0<y0≤
≤y0<0或0<y0≤![]() .
.
綜上,y0的取值范圍是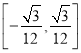 .
.


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】給出以下命題,
①命題“若![]() ,則
,則![]() 或
或![]() ”為真命題;
”為真命題;
②命題“若![]() ,則
,則![]() ”的否命題為真命題;
”的否命題為真命題;
③若平面![]() 上不共線的三個點到平面
上不共線的三個點到平面![]() 距離相等,則
距離相等,則![]()
④若![]() ,
,![]() 是兩個不重合的平面,直線
是兩個不重合的平面,直線![]() ,命題
,命題![]() ,命題
,命題![]() ,則
,則![]() 是
是![]() 的必要不充分條件;
的必要不充分條件;
⑤平面![]() 過正方體
過正方體![]() 的三個頂點
的三個頂點![]() ,且
,且![]() 與底面
與底面![]() 的交線為
的交線為![]() ,則
,則![]() ∥
∥![]() ;
;
其中,真命題的序號是______
查看答案和解析>>
科目:高中數學 來源: 題型:
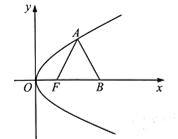
【題目】在平面直角坐標系![]() 中,已知點F為拋物線
中,已知點F為拋物線![]() 的焦點,點A在拋物線E上,
的焦點,點A在拋物線E上,
點B在x軸上,且![]() 是邊長為2的等邊三角形。
是邊長為2的等邊三角形。
(1)求拋物線E的方程;
(2)設C是拋物線E上的動點,直線![]() 為拋物線E在點C處的切線,求點B到直線
為拋物線E在點C處的切線,求點B到直線![]() 距離的最小值,并求此時點C的坐標。
距離的最小值,并求此時點C的坐標。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場對顧客實行購物優惠活動,規定 :一次購物總額
1)如果不超過500元,那么不予優惠;
2)如果超過500元但不超過1000元,那么超過500元部分按標價給予8折優惠;
3)如果超過1000元,那么其中超過500不超過1000元給予8折優惠,超過1000元部分給予5折優惠.設一次購物標價總額為x元,優惠后實際付款額為f(x)元.
(1)試寫出f(x)的解析式;
(2)如果某顧客實際付款額為1600元,在這次優惠活動中他實際付款額比購物標價總額少支出多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過點A(0,1)且斜率為k的直線l與圓C:(x-2)2+(y-3)2=1交于M,N兩點.
(1)求k的取值范圍;
(2)若![]() =12,其中O為坐標原點,求|MN|.
=12,其中O為坐標原點,求|MN|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于圓周率![]() ,數學發展史上出現過許多很有創意的求法,如著名的蒲豐實驗和查理斯實驗.受其啟發,我們也可以通過設計下面的實驗來估計
,數學發展史上出現過許多很有創意的求法,如著名的蒲豐實驗和查理斯實驗.受其啟發,我們也可以通過設計下面的實驗來估計![]() 的值:先請
的值:先請![]() 名同學,每人隨機寫下一個都小于1的正實數對
名同學,每人隨機寫下一個都小于1的正實數對![]() ;再統計兩數能與1構成鈍角三角形三邊的數對
;再統計兩數能與1構成鈍角三角形三邊的數對![]() 的個數
的個數![]() ;最后再根據統計數
;最后再根據統計數![]() 來估計
來估計![]() 的值.假如統計結果是
的值.假如統計結果是![]() ,那么可以估計
,那么可以估計![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com