
【題目】某動漫影視制作公司長期堅持文化自信,不斷挖掘中華優秀傳統文化中的動漫題材,創作出一批又一批的優秀動漫影視作品,獲得市場和廣大觀眾的一致好評,同時也為公司贏得豐厚的利潤.該公司![]() 年至
年至![]() 年的年利潤
年的年利潤![]() 關于年份代號
關于年份代號![]() 的統計數據如下表(已知該公司的年利潤與年份代號線性相關).
的統計數據如下表(已知該公司的年利潤與年份代號線性相關).
年份 |
|
|
|
|
|
|
|
年份代號 |
|
|
|
|
|
|
|
年利潤 |
|
|
|
|
|
|
|
(Ⅰ)求![]() 關于
關于![]() 的線性回歸方程,并預測該公司
的線性回歸方程,并預測該公司![]() 年(年份代號記為
年(年份代號記為![]() )的年利潤;
)的年利潤;
(Ⅱ)當統計表中某年年利潤的實際值大于由(Ⅰ)中線性回歸方程計算出該年利潤的估計值時,稱該年為![]() 級利潤年,否則稱為
級利潤年,否則稱為![]() 級利潤年.將(Ⅰ)中預測的該公司
級利潤年.將(Ⅰ)中預測的該公司![]() 年的年利潤視作該年利潤的實際值,現從
年的年利潤視作該年利潤的實際值,現從![]() 年至
年至![]() 年這
年這![]() 年中隨機抽取
年中隨機抽取![]() 年,求恰有
年,求恰有![]() 年為
年為![]() 級利潤年的概率.
級利潤年的概率.
參考公式: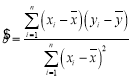 ,
,![]() .
.
【答案】(Ⅰ)![]() ,該公司
,該公司![]() 年年利潤的預測值為
年年利潤的預測值為![]() 億元;(Ⅱ)
億元;(Ⅱ)![]() .
.
【解析】
(Ⅰ)求出![]() 和
和![]() 的值,將表格中的數據代入最小二乘法公式,求得
的值,將表格中的數據代入最小二乘法公式,求得![]() 和
和![]() 的值,進而可求得
的值,進而可求得![]() 關于
關于![]() 的線性回歸方程,然后將
的線性回歸方程,然后將![]() 代入回歸直線方程,可得出該公司
代入回歸直線方程,可得出該公司![]() 年年利潤的估計值;
年年利潤的估計值;
(Ⅱ)利用(Ⅰ)中的回歸直線方程計算出從![]() 年至
年至![]() 年這
年這![]() 年被評為
年被評為![]() 級利潤年的年數,然后利用組合計數原理結合古典概型的概率可得出所求事件的概率.
級利潤年的年數,然后利用組合計數原理結合古典概型的概率可得出所求事件的概率.
(Ⅰ)根據表中數據,計算可得![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,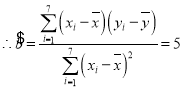 ,
,
![]() ,
,![]() 關于
關于![]() 的線性回歸方程為
的線性回歸方程為![]() .
.
將![]() 代入回歸方程得
代入回歸方程得![]() (億元),
(億元),
![]() 該公司
該公司![]() 年的年利潤的預測值為
年的年利潤的預測值為![]() 億元.
億元.
(Ⅱ)由(Ⅰ)可知![]() 年至
年至![]() 年的年利潤的估計值分別為
年的年利潤的估計值分別為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() (單位:億元),其中實際利潤大于相應估計值的有
(單位:億元),其中實際利潤大于相應估計值的有![]() 年.
年.
故這![]() 年中被評為
年中被評為![]() 級利潤年的有
級利潤年的有![]() 年,評為
年,評為![]() 級利潤年的有
級利潤年的有![]() 年.
年.
記“從![]() 年至
年至![]() 年這
年這![]() 年的年利潤中隨機抽取
年的年利潤中隨機抽取![]() 年,恰有
年,恰有![]() 年為
年為![]() 級利潤年”的概率為
級利潤年”的概率為![]() ,
,![]() .
.


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:高中數學 來源: 題型:
【題目】冠狀病毒是一個大型病毒家族,己知可引起感冒以及中東呼吸綜合征(![]() )和嚴重急性呼吸綜合征(
)和嚴重急性呼吸綜合征(![]() )等較嚴重疾病.而今年出現在湖北武漢的新型冠狀病毒(
)等較嚴重疾病.而今年出現在湖北武漢的新型冠狀病毒(![]() )是以前從未在人體中發現的冠狀病毒新毒株.人感染了新型冠狀病毒后常見體征有呼吸道癥狀、發熱、咳嗽、氣促和呼吸困難等.在較嚴重病例中,感染可導致肺炎、嚴重急性呼吸綜合征、腎衰竭,甚至死亡.
)是以前從未在人體中發現的冠狀病毒新毒株.人感染了新型冠狀病毒后常見體征有呼吸道癥狀、發熱、咳嗽、氣促和呼吸困難等.在較嚴重病例中,感染可導致肺炎、嚴重急性呼吸綜合征、腎衰竭,甚至死亡.
某醫院為篩查冠狀病毒,需要檢驗血液是否為陽性,現有n(![]() )份血液樣本,有以下兩種檢驗方式:
)份血液樣本,有以下兩種檢驗方式:
方式一:逐份檢驗,則需要檢驗n次.
方式二:混合檢驗,將其中k(![]() 且
且![]() )份血液樣本分別取樣混合在一起檢驗.
)份血液樣本分別取樣混合在一起檢驗.
若檢驗結果為陰性,這k份的血液全為陰性,因而這k份血液樣本只要檢驗一次就夠了,如果檢驗結果為陽性,為了明確這k份血液究竟哪幾份為陽性,就要對這k份再逐份檢驗,此時這k份血液的檢驗次數總共為![]() .
.
假設在接受檢驗的血液樣本中,每份樣本的檢驗結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為p(![]() ).現取其中k(
).現取其中k(![]() 且
且![]() )份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數為
)份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數為![]() ,采用混合檢驗方式,樣本需要檢驗的總次數為
,采用混合檢驗方式,樣本需要檢驗的總次數為![]() .
.
(1)若![]() ,試求p關于k的函數關系式
,試求p關于k的函數關系式![]() ;
;
(2)若p與干擾素計量![]() 相關,其中
相關,其中![]() (
(![]() )是不同的正實數,
)是不同的正實數,
滿足![]() 且
且![]() (
(![]() )都有
)都有![]() 成立.
成立.
(i)求證:數列![]() 等比數列;
等比數列;
(ii)當![]() 時,采用混合檢驗方式可以使得樣本需要檢驗的總次數的期望值比逐份檢驗的總次數的期望值更少,求k的最大值
時,采用混合檢驗方式可以使得樣本需要檢驗的總次數的期望值比逐份檢驗的總次數的期望值更少,求k的最大值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 、點
、點![]() 及拋物線
及拋物線![]() .
.
(1)若直線![]() 過點
過點![]() 及拋物線
及拋物線![]() 上一點
上一點![]() ,當
,當![]() 最大時求直線
最大時求直線![]() 的方程;
的方程;
(2)![]() 軸上是否存在點
軸上是否存在點![]() ,使得過點
,使得過點![]() 的任一條直線與拋物線
的任一條直線與拋物線![]() 交于點
交于點![]() ,且點
,且點![]() 到直線
到直線![]() 的距離相等?若存在,求出點
的距離相等?若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了鼓勵運動提高所有用戶的身體素質,特推出一款運動計步數的軟件,所有用戶都可以通過每天累計的步數瓜分紅包,大大增加了用戶走步的積極性,所以該軟件深受廣大用戶的歡迎.該公司為了研究“日平均走步數和性別是否有關”,統計了2019年1月份所有用戶的日平均步數,規定日平均步數不少于8000的為“運動達人”,步數在8000以下的為“非運動達人”,采用按性別分層抽樣的方式抽取了100個用戶,得到如下列聯表:
運動達人 | 非運動達人 | 總計 | |
男 | 35 | 60 | |
女 | 26 | ||
總計 | 100 |
(1)(i)將![]() 列聯表補充完整;
列聯表補充完整;
(ii)據此列聯表判斷,能否有![]() 的把握認為“日平均走步數和性別是否有關”?
的把握認為“日平均走步數和性別是否有關”?
(2)從樣本中的運動達人中抽取7人參加“幸運抽獎”活動,通過抽獎共產生2位幸運用戶,求這2位幸運用戶恰好男用戶和女用戶各一位的概率.
附:
|
|
|
|
|
|
|
|
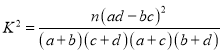
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩焦點與短軸的一個端點的連線構成面積為
的兩焦點與短軸的一個端點的連線構成面積為![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求橢圓E的標準方程;
(2)直線![]() 與橢圓交于點A、B,線段
與橢圓交于點A、B,線段![]() 的中點為M,射線MO與橢圓交于點P,點O為
的中點為M,射線MO與橢圓交于點P,點O為![]() 的重心,試問:
的重心,試問:![]() 的面積S是否為定值,若是,求出這個值;若不是,求S的取值范圍.
的面積S是否為定值,若是,求出這個值;若不是,求S的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com