
【題目】某電視臺舉行一個比賽類型的娛樂節目,![]() 兩隊各有六名選手參賽,將他們首輪的比賽成績作為樣本數據,繪制成莖葉圖如圖所示,為了增加節目的趣味性,主持人故意將
兩隊各有六名選手參賽,將他們首輪的比賽成績作為樣本數據,繪制成莖葉圖如圖所示,為了增加節目的趣味性,主持人故意將![]() 隊第六位選手的成績沒有給出,并且告知大家
隊第六位選手的成績沒有給出,并且告知大家![]() 隊的平均分比
隊的平均分比![]() 隊的平均分多4分,同時規定如果某位選手的成績不少于21分,則獲得“晉級”.
隊的平均分多4分,同時規定如果某位選手的成績不少于21分,則獲得“晉級”.
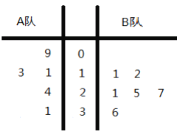
(1)主持人從![]() 隊所有選手成績中隨機抽取2個,求至少有一個為“晉級”的概率;
隊所有選手成績中隨機抽取2個,求至少有一個為“晉級”的概率;
(2)主持人從![]() 兩隊所有選手成績中分別隨機抽取2個,記抽取到“晉級”選手的總人數為
兩隊所有選手成績中分別隨機抽取2個,記抽取到“晉級”選手的總人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
【答案】(1)![]() ;(2)分布列見解析,2.
;(2)分布列見解析,2.
【解析】
(1)先由題意求得![]() 隊第六位選手的成績,則可得
隊第六位選手的成績,則可得![]() 隊中成績不少于21分的有2個,再利用對立事件求概率即可;
隊中成績不少于21分的有2個,再利用對立事件求概率即可;
(2)由(1)可得![]() 隊中所有選手成績能“晉級”的有2個,
隊中所有選手成績能“晉級”的有2個,![]() 隊中所有選手成績能“晉級”的有4個,則
隊中所有選手成績能“晉級”的有4個,則![]() 的可能取值有
的可能取值有![]() ,分別討論求解即可得到分布列,利用公式求得期望即可
,分別討論求解即可得到分布列,利用公式求得期望即可
(1)![]() 隊選手的平均分為
隊選手的平均分為![]() ,
,
設![]() 隊第6位選手的成績為
隊第6位選手的成績為![]() 分,因為
分,因為![]() 隊的平均分比
隊的平均分比![]() 隊的平均分多4分,
隊的平均分多4分,
則![]() ,得
,得![]() ,
,
則![]() 隊中成績不少于21分的有2個,
隊中成績不少于21分的有2個,
因為從中抽取2個至少有一個為“晉級”的對立事件為兩人都沒有“晉級”,
則概率![]()
(2)由(1),![]() 隊中所有選手成績能“晉級”的有2個,
隊中所有選手成績能“晉級”的有2個,![]() 隊中所有選手成績能“晉級”的有4個,則
隊中所有選手成績能“晉級”的有4個,則![]() 的可能取值有
的可能取值有![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
∴![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
∴![]()


科目:高中數學 來源: 題型:
【題目】近來天氣變化無常,陡然升溫、降溫幅度大于![]() 的天氣現象出現增多.陡然降溫幅度大于
的天氣現象出現增多.陡然降溫幅度大于![]() 容易引起幼兒傷風感冒疾病.為了解傷風感冒疾病是否與性別有關,在某婦幼保健院隨機對人院的
容易引起幼兒傷風感冒疾病.為了解傷風感冒疾病是否與性別有關,在某婦幼保健院隨機對人院的![]() 名幼兒進行調查,得到了如下的列聯表,若在全部
名幼兒進行調查,得到了如下的列聯表,若在全部![]() 名幼兒中隨機抽取
名幼兒中隨機抽取![]() 人,抽到患傷風感冒疾病的幼兒的概率為
人,抽到患傷風感冒疾病的幼兒的概率為![]() ,
,
(1)請將下面的列聯表補充完整;
患傷風感冒疾病 | 不患傷風感冒疾病 | 合計 | |
男 | 25 | ||
女 | 20 | ||
合計 | 100 |
(2)能否在犯錯誤的概率不超過![]() 的情況下認為患傷風感冒疾病與性別有關?說明你的理由;
的情況下認為患傷風感冒疾病與性別有關?說明你的理由;
(3)已知在患傷風感冒疾病的![]() 名女性幼兒中,有
名女性幼兒中,有![]() 名又患黃痘病.現在從患傷風感冒疾病的
名又患黃痘病.現在從患傷風感冒疾病的![]() 名女性中,選出
名女性中,選出![]() 名進行其他方面的排查,記選出患黃痘病的女性人數為
名進行其他方面的排查,記選出患黃痘病的女性人數為![]() ,求
,求![]() 的分布列以及數學期望.下面的臨界值表供參考:
的分布列以及數學期望.下面的臨界值表供參考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式: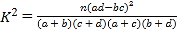 ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() 且側棱
且側棱![]() 其中
其中![]() 為
為![]() 的
的![]() 交點.
交點.
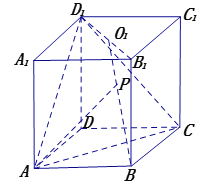
(1)求點![]() 到平面
到平面![]() 的距離;
的距離;
(2)在線段![]() 上,是否存在一個點
上,是否存在一個點![]() ,使得直線
,使得直線![]() 與
與![]() 垂直?若存在,求出線段
垂直?若存在,求出線段![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,游客從某旅游景區的景點A處下山至C處有兩種路徑.一種是從A沿直線步行到C,另一種是先從A沿索道乘纜車到B,然后從B沿直線步行到C.現有甲、乙兩位游客從A處下山,甲沿AC勻速步行,速度為50 m/min.在甲出發2 min后,乙從A乘纜車到B,在B處停留1 min后,再從B勻速步行到C.假設纜車勻速直線運行的速度為130 m/min,山路AC長為1260 m,經測量,cos A=![]() ,cos C=
,cos C=![]()
(1)求索道AB的長;
(2)問乙出發多少分鐘后,乙在纜車上與甲的距離最短?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個不相等的非零向量![]() ,兩組向量
,兩組向量![]() 和
和![]() 均由2個
均由2個![]() 和3個
和3個![]() 排列而成,記
排列而成,記![]() ,
,![]() 表示
表示![]() 所有可能取值中的最小值,則下列命題中
所有可能取值中的最小值,則下列命題中
(1)![]() 有5個不同的值;(2)若
有5個不同的值;(2)若![]() 則
則![]() 與
與![]() 無關;(3)若
無關;(3)若![]() ,則
,則![]() 與
與![]() 無關;(4)若
無關;(4)若![]() ,則
,則![]() ;(5)若
;(5)若![]() ,
,![]() ,則
,則![]() 與
與![]() 的夾角為
的夾角為![]() .正確的是( )
.正確的是( )
A.(1)(2)B.(2)(4)C.(3)(5)D.(1)(4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了配合今年上海迪斯尼游園工作,某單位設計了統計人數的數學模型![]() :以
:以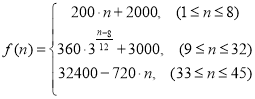 表示第
表示第![]() 個時刻進入園區的人數;以
個時刻進入園區的人數;以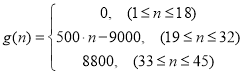 表示第
表示第![]() 個時刻離開園區的人數.設定以
個時刻離開園區的人數.設定以![]() 分鐘為一個計算單位,上午
分鐘為一個計算單位,上午![]() 點
點![]() 分作為第
分作為第![]() 個計算人數單位,即
個計算人數單位,即![]() ;
;![]() 點
點![]() 分作為第
分作為第![]() 個計算單位,即
個計算單位,即![]() ;依次類推,把一天內從上午
;依次類推,把一天內從上午![]() 點到晚上
點到晚上![]() 點
點![]() 分分成
分分成![]() 個計算單位(最后結果四舍五入,精確到整數).
個計算單位(最后結果四舍五入,精確到整數).
(1)試計算當天![]() 點至
點至![]() 點這一小時內,進入園區的游客人數
點這一小時內,進入園區的游客人數![]() 、離開園區的游客人數
、離開園區的游客人數![]() 各為多少?
各為多少?
(2)假設當日園區游客總人數達到或超過![]() 萬時,園區將采取限流措施.該單位借助該數學模型知曉當天
萬時,園區將采取限流措施.該單位借助該數學模型知曉當天![]() 點(即
點(即![]() )時,園區總人數會達到最高,請問當日是否要采取限流措施?說明理由.
)時,園區總人數會達到最高,請問當日是否要采取限流措施?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某人打算做一個正四棱錐形的金字塔模型,先用木料搭邊框,再用其他材料填充,已知金字塔的每一條棱和邊都相等.
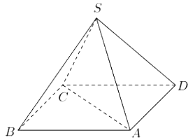
(1)求證:直線AC垂直于直線SD;
(2)若搭邊框共使用木料24米,則需要多少立方米的填充材料才能將整個金字塔內部填滿?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (其中
(其中![]() )的最小周期為
)的最小周期為![]() .
.
(1)求![]() 的值及
的值及![]() 的單調遞增區間;
的單調遞增區間;
(2)將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位,再將圖象上各點的橫坐標縮短為原來的
個單位,再將圖象上各點的橫坐標縮短為原來的![]() (縱坐標不變)得到函數
(縱坐標不變)得到函數![]() 的圖象,若關于x的方程
的圖象,若關于x的方程![]() 在區間
在區間![]() 上有且只有一個解,求實數m的取值范圍.
上有且只有一個解,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com