
【題目】已知函數![]() .
.
![]() Ⅰ
Ⅰ![]() 若曲線
若曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直,求函數
垂直,求函數![]() 的單調區間;
的單調區間;
![]() Ⅱ
Ⅱ![]() 若對于
若對于![]() 都有
都有![]() 成立,試求a的取值范圍;
成立,試求a的取值范圍;
![]() Ⅲ
Ⅲ![]() 記
記![]() 當
當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上有兩個零點,求實數b的取值范圍.
上有兩個零點,求實數b的取值范圍.
【答案】解: (I) 直線![]() 的斜率為1.
的斜率為1.
函數![]() 的定義域為
的定義域為![]() ,
,
因為![]() ,所以
,所以![]() ,所以
,所以![]() .
.
所以![]() .
.![]() .
.
由![]() 解得
解得![]() ;由
;由![]() 解得
解得![]() .
.
所以![]() 的單調增區間是
的單調增區間是![]() ,單調減區間是
,單調減區間是![]() . ……………………4分
. ……………………4分
(II)![]() ,
,
由![]() 解得
解得![]() ;由
;由![]() 解得
解得![]() .
.
所以![]() 在區間
在區間![]() 上單調遞增,在區間
上單調遞增,在區間![]() 上單調遞減.
上單調遞減.
所以當![]() 時,函數
時,函數![]() 取得最小值,
取得最小值,![]() .
.
因為對于![]() 都有
都有![]() 成立,
成立,
所以![]() 即可.
即可.
則![]() . 由
. 由![]() 解得
解得![]() .
.
所以![]() 的取值范圍是
的取值范圍是![]() . ………………………………8分
. ………………………………8分
(III)依題得![]() ,則
,則![]() .
.
由![]() 解得
解得![]() ;由
;由![]() 解得
解得![]() .
.
所以函數![]() 在區間
在區間![]() 為減函數,在區間
為減函數,在區間![]() 為增函數.
為增函數.
又因為函數![]() 在區間
在區間![]() 上有兩個零點,所以
上有兩個零點,所以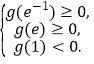
解得![]() .
.
所以![]() 的取值范圍是
的取值范圍是![]() . ……………………………………13分
. ……………………………………13分
【解析】
![]() Ⅰ
Ⅰ![]() 求出函數的定義域,在定義域內,求出導數大于0的區間,即為函數的增區間,求出導數小于0的區間即為函數的減區間;
求出函數的定義域,在定義域內,求出導數大于0的區間,即為函數的增區間,求出導數小于0的區間即為函數的減區間;![]() Ⅱ
Ⅱ![]() 根據函數的單調區間求出函數的最小值,要使
根據函數的單調區間求出函數的最小值,要使![]() 恒成立,需使函數的最小值大于
恒成立,需使函數的最小值大于![]() ,從而求得a的取值范圍;
,從而求得a的取值范圍;![]() Ⅲ
Ⅲ![]() 利用導數的符號求出單調區間,再根據函數
利用導數的符號求出單調區間,再根據函數![]() 在區間
在區間![]() 上有兩個零點,得到
上有兩個零點,得到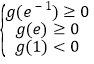 ,解出實數b的取值范圍.
,解出實數b的取值范圍.
![]() Ⅰ
Ⅰ![]() 直線
直線![]() 的斜率為1,函數
的斜率為1,函數![]() 的定義域為
的定義域為![]() ,
,
因為![]() ,所以,
,所以,![]() ,所以,
,所以,![]() .
.
所以,![]() ,
,![]() 由
由 ![]() 解得
解得![]() ;由
;由![]() 解得
解得![]() .
.
所以![]() 的單調增區間是
的單調增區間是![]() ,單調減區間是
,單調減區間是![]() .
.
![]() Ⅱ
Ⅱ![]()
![]() ,由
,由![]() ,解得
,解得![]() ;由
;由![]() 解得
解得![]() .
.
所以,![]() 在區間
在區間![]() 上單調遞增,在區間
上單調遞增,在區間![]() 上單調遞減.
上單調遞減.
所以,當![]() 時,函數
時,函數![]() 取得最小值,
取得最小值,![]() 因為對于
因為對于![]() 都有
都有![]() 成立,
成立,
所以,![]() 即可
即可![]() 則
則![]() 由
由![]() 解得
解得![]() .
.
所以,a的取值范圍是![]() .
.
![]() Ⅲ
Ⅲ![]() 依題得
依題得![]() ,則
,則![]() .
.
由![]() 解得
解得![]() ; 由
; 由![]() 解得
解得![]() .
.
所以函數![]() 在區間
在區間![]() 為減函數,在區間
為減函數,在區間![]() 為增函數.
為增函數.
又因為函數![]() 在區間
在區間![]() 上有兩個零點,所以
上有兩個零點,所以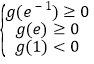 ,
,
解得![]() 所以,b的取值范圍是
所以,b的取值范圍是![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設點A,B的坐標分別為(-2,0),(2,0)直線AM,BM相交于點M,且它們的斜率之積是-![]() .
.
(1)求點M的軌跡E的方程;
(2)設直線l:y=kx與E交于C,D兩點,F1(-1,0),F2(1,0),若E上存在點P,使得![]() ,求實數k的取值范圍.
,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商店銷售某海鮮,統計了春節前后50天該海鮮的需求量![]() (
(![]() ,單位:公斤),其頻率分布直方圖如圖所示,該海鮮每天進貨1次,商店每銷售1公斤可獲利50元;若供大于求,剩余的削價處理,每處理1公斤虧損10元;若供不應求,可從其它商店調撥,銷售1公斤可獲利30元.假設商店每天該海鮮的進貨量為14公斤,商店的日利潤為
,單位:公斤),其頻率分布直方圖如圖所示,該海鮮每天進貨1次,商店每銷售1公斤可獲利50元;若供大于求,剩余的削價處理,每處理1公斤虧損10元;若供不應求,可從其它商店調撥,銷售1公斤可獲利30元.假設商店每天該海鮮的進貨量為14公斤,商店的日利潤為![]() 元.
元.

(1)求商店日利潤![]() 關于需求量
關于需求量![]() 的函數表達式;
的函數表達式;
(2)假設同組中的每個數據用該組區間的中點值代替.
①求這50天商店銷售該海鮮日利潤的平均數;
②估計日利潤在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了解全校高中學生五一小長假參加實踐活動的情況,抽查了100名學生,統計他們假期參加實踐活動的時間,繪成的頻率分布直方圖如圖所示.
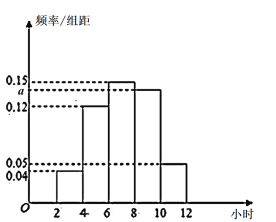
(1)估計這100名學生參加實踐活動時間的眾數、中位數和平均數.
(2)估計這100名學生參加實踐活動時間的上四分位數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() ,現以極點
,現以極點![]() 為原點,極軸為
為原點,極軸為![]() 軸的非負半軸建立平面直角坐標系,曲線
軸的非負半軸建立平面直角坐標系,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)求直線![]() 的直角坐標方程和曲線
的直角坐標方程和曲線![]() 的普通方程;
的普通方程;
(2)若曲線![]() 為曲線
為曲線![]() 關于直線
關于直線![]() 的對稱曲線,點
的對稱曲線,點![]() 分別為曲線
分別為曲線![]() 、曲線
、曲線![]() 上的動點,點
上的動點,點![]() 坐標為
坐標為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,攝影愛好者在某公園A處,發現正前方B處有一立柱,測得立柱頂端O的仰角和立柱底部B的俯角均為![]() ,已知攝影愛好者的身高約為
,已知攝影愛好者的身高約為![]() 米(將眼睛S距地面的距離SA按
米(將眼睛S距地面的距離SA按![]() 米處理).
米處理).
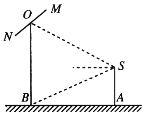
(1)求攝影愛好者到立柱的水平距離AB和立柱的高度OB;
(2)立柱的頂端有一長為2米的彩桿MN,且MN繞其中點O在攝影愛好者與立柱所在的平面內旋轉.在彩桿轉動的任意時刻,攝影愛好者觀察彩桿MN的視角![]() (設為
(設為![]() )是否存在最大值?若存在,請求出
)是否存在最大值?若存在,請求出![]() 取最大值時
取最大值時![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將![]() 這9個正整數分別寫在三張卡片上,要求每一張卡片上的任意兩數之差都不在這張卡片上,現在第一張卡片上已經寫有
這9個正整數分別寫在三張卡片上,要求每一張卡片上的任意兩數之差都不在這張卡片上,現在第一張卡片上已經寫有![]() 和
和![]() ,第二張卡片上寫有
,第二張卡片上寫有![]() ,第三張卡片上寫有
,第三張卡片上寫有![]() ,則
,則![]() 應該寫在第__________張卡片上;第三張卡片上的所有書組成的集合是__________.
應該寫在第__________張卡片上;第三張卡片上的所有書組成的集合是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了解畢業班學業水平考試學生的數學考試情況,抽取了該校100名學生的數學成績,將所有數據整理后,畫出了樣頻率分布直方圖(所圖所示),若第1組第9組的頻率各為x.

(1)求x的值,并估計這次學業水平考試數學成績的眾數;
(2)若全校有1500名學生參加了此次考試,估計成績在[80,100)分內的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com