
【題目】在四棱錐![]() 的底面
的底面![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中點,且
的中點,且![]()

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ,若存在指出點
,若存在指出點![]() 的位置,若不存在請說明理由.
的位置,若不存在請說明理由.
科目:高中數(shù)學 來源: 題型:
【題目】關(guān)于圓周率π,數(shù)學發(fā)展史上出現(xiàn)過許多很有創(chuàng)意的求法,如著名的浦豐實驗和查理斯實驗.受其啟發(fā),我們也可以通過設計下面的實驗來估計![]() 的值:先請全校
的值:先請全校![]() 名同學每人隨機寫下一個都小于
名同學每人隨機寫下一個都小于![]() 的正實數(shù)對
的正實數(shù)對![]() ;再統(tǒng)計兩數(shù)能與
;再統(tǒng)計兩數(shù)能與![]() 構(gòu)成鈍角三角形三邊的數(shù)對
構(gòu)成鈍角三角形三邊的數(shù)對![]() 的個數(shù)
的個數(shù)![]() ;最后再根據(jù)統(tǒng)計數(shù)
;最后再根據(jù)統(tǒng)計數(shù)![]() 估計
估計![]() 的值,那么可以估計
的值,那么可以估計![]() 的值約為( )
的值約為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,過
,過![]() 作
作![]() 軸的垂線交橢圓
軸的垂線交橢圓![]() 于點
于點![]() (點
(點![]() 在
在![]() 軸上方),斜率為
軸上方),斜率為![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() 兩點,過點
兩點,過點![]() 作直線
作直線![]() 交橢圓
交橢圓![]() 于點
于點![]() ,且
,且![]() ,直線
,直線![]() 交
交![]() 軸于點
軸于點![]() .
.
(1)設橢圓![]() 的離心率為
的離心率為![]() ,當點
,當點![]() 為橢圓
為橢圓![]() 的右頂點時,
的右頂點時,![]() 的坐標為
的坐標為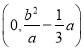 ,求
,求![]() 的值.
的值.
(2)若橢圓![]() 的方程為
的方程為![]() ,且
,且![]() ,是否存在
,是否存在![]() 使得
使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】光伏發(fā)電是將光能直接轉(zhuǎn)變?yōu)殡娔艿囊环N技術(shù),具有資源的充足性及潛在的經(jīng)濟性等優(yōu)點,在長期的能源戰(zhàn)略中具有重要地位,2015年起,國家能源局、國務院扶貧辦聯(lián)合在6省的30個縣開展光伏扶貧試點,在某縣居民中隨機抽取50戶,統(tǒng)計其年用量得到以下統(tǒng)計表.以樣本的頻率作為概率.
用電量(單位:度) |
|
|
|
|
|
戶數(shù) | 7 | 8 | 15 | 13 | 7 |
(Ⅰ)在該縣居民中隨機抽取10戶,記其中年用電量不超過600度的戶數(shù)為![]() ,求
,求![]() 的數(shù)學期望;
的數(shù)學期望;
(Ⅱ)在總結(jié)試點經(jīng)驗的基礎上,將村級光伏電站穩(wěn)定為光伏扶貧的主推方式.已知該縣某自然村有居民300戶.若計劃在該村安裝總裝機容量為300千瓦的光伏發(fā)電機組,該機組所發(fā)電量除保證該村正常用電外,剩余電量國家電網(wǎng)以0.8元/度的價格進行收購.經(jīng)測算每千瓦裝機容量的發(fā)電機組年平均發(fā)電1000度,試估計該機組每年所發(fā)電量除保證正常用電外還能為該村創(chuàng)造直接受益多少元?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】科赫曲線是一種外形像雪花的幾何曲線,一段科赫曲線可以通過下列操作步驟構(gòu)造得到,任畫一條線段,然后把它均分成三等分,以中間一段為邊向外作正三角形,并把中間一段去掉,這樣,原來的一條線段就變成了4條小線段構(gòu)成的折線,稱為“一次構(gòu)造”;用同樣的方法把每條小線段重復上述步驟,得到16條更小的線段構(gòu)成的折線,稱為“二次構(gòu)造”,…,如此進行“![]() 次構(gòu)造”,就可以得到一條科赫曲線.若要在構(gòu)造過程中使得到的折線的長度達到初始線段的1000倍,則至少需要通過構(gòu)造的次數(shù)是( ).(取
次構(gòu)造”,就可以得到一條科赫曲線.若要在構(gòu)造過程中使得到的折線的長度達到初始線段的1000倍,則至少需要通過構(gòu)造的次數(shù)是( ).(取![]() ,
,![]() )
)
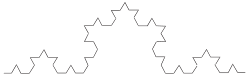
A.16B.17C.24D.25
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為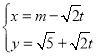 (其中
(其中![]() 為參數(shù),
為參數(shù),![]() ).以坐標原點
).以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
,![]() 被
被![]() 截得的弦長為
截得的弦長為![]() .
.
(1)求實數(shù)![]() 的值;
的值;
(2)設![]() 與
與![]() 交于點
交于點![]() ,
,![]() ,若點
,若點![]() 的坐標為
的坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() .底面
.底面![]() 為梯形,
為梯形,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
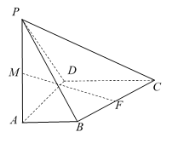
(1)求證:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)若![]() 是棱
是棱![]() 的中點,求證:對于棱
的中點,求證:對于棱![]() 上任意一點
上任意一點![]() ,
,![]() 與
與![]() 都不平行.
都不平行.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知雙曲線E![]() 的左、右焦點分別為F1,F2,P是雙曲線E上的一點,且|PF2|=2|PF1|,若直線PF2與雙曲線E的漸近線交于點M,且M為PF2的中點,則雙曲線E的漸近線方程為( )
的左、右焦點分別為F1,F2,P是雙曲線E上的一點,且|PF2|=2|PF1|,若直線PF2與雙曲線E的漸近線交于點M,且M為PF2的中點,則雙曲線E的漸近線方程為( )
A.y=±![]() B.y=±
B.y=±![]() C.y=±2xD.y=±3x
C.y=±2xD.y=±3x
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com