
杭州學軍中學高三年級2006學年第三次月考
數學試卷(文科)
一、選擇題:(本大題共12小題,每小題5分,共60分。在每小題給出的四個選項中,只有一項是符合題目要求的)
1.已知集合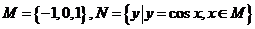 ,則
,則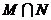 是
( )
是
( )
(A)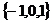 (B)
(B)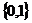 (C)
(C)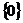 (D)
(D)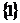
2.若條件 ,條件
,條件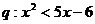 ,則
,則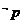 是
是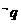 的txjy
的txjy
(A)必要不充分條件 (B)充分不必要條件
(C)充要條件 (D)既不充分又不必要條件
3.定義域為R的函數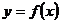 的值域為
的值域為 ,則函數
,則函數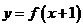 的值域為 ( )
的值域為 ( )
(A) (B)
(B)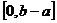 (C)
(C) (D)
(D)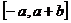
4.函數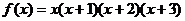 …
…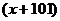 在
在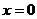 處導數值為 ( )
處導數值為 ( )
(A)0 (B)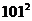 (C)1
(D)
(C)1
(D)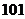 !
!
5.設函數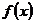 是定義在R上的以3為周期的奇函數,若
是定義在R上的以3為周期的奇函數,若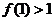 ,
, ,
,
則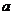 取值范圍是
( )
取值范圍是
( )
(A)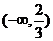 (B)
(B)
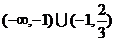
(C) 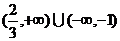 (D)
(D)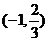
6.下列命題正確的是( )
(A)函數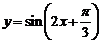 在區間
在區間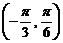 內單調遞增
內單調遞增
(B)函數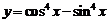 的最小正周期為
的最小正周期為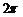
(C)函數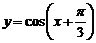 的圖像是關于點
的圖像是關于點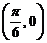 成中心對稱的圖形
成中心對稱的圖形
(D)函數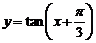 的圖像是關于直線
的圖像是關于直線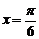 成軸對稱的圖形
成軸對稱的圖形
7.已知等比數列 的公比
的公比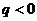 ,前
,前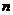 項的和為
項的和為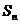 ,則
,則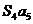 與
與 的大小關系
的大小關系
(A) (B)
(B)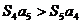 (C)
(C)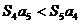 (D)不確定
(D)不確定
8.袋中有40個小球,其中紅色球16個、藍色球12個、白色球8個、黃色球4個,從中隨機抽取10球作成一個樣本,則這個樣本恰好是按分層抽樣得到的概率為 ( )
(A)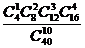 (B)
(B)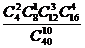 (C)
(C)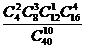 (D)
(D)
9.使關于 的不等式
的不等式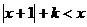 有解的實數
有解的實數 的取值范圍是
( )
的取值范圍是
( )
(A)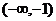 (B)
(B) (C)
(C)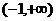 (D)
(D)
10.已知函數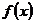 是定義在R上的不恒為零的函數,且對于任意的
是定義在R上的不恒為零的函數,且對于任意的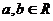 ,滿足
,滿足
下列結論:①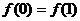 ,②
,②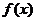 為偶函數;③數列
為偶函數;③數列 為等比數列;④數列
為等比數列;④數列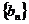 為等差數列。其中正確的是
( )
為等差數列。其中正確的是
( )
(A)①② (B)②④ (C)①③④ (D)①②③④
二、填空題:本大題共4小題,每小題4分,共16分。
11.若指數函數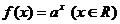 的部分對應值如下表
的部分對應值如下表

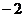
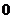
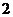
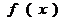

1
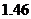
則不等式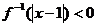 的解集為____________。
的解集為____________。
12.函數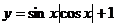 的最小正周期與最大值的和為 。
的最小正周期與最大值的和為 。
13.設等差數列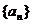 的前n項和為Sn,若
的前n項和為Sn,若 ,則
,則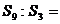 。
。
14.已知奇函數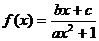 有最大值
有最大值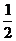 , 且
, 且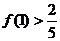 , 其中實數
, 其中實數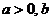 是正整數.
是正整數.
則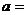 ____________
____________ 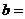 .
. 。
。

 杭州學軍中學高三年級2006學年第三次月考
杭州學軍中學高三年級2006學年第三次月考
數學答卷(文科)
座位號
題號
1
2
3
4
5
6
7
8
9
10
答案
二、填空題:本大題共4小題;每小題4分,共16分。
11. 12.
13. 14.
三、解答題:本大題共6小題,每小題14分,共84分。解答應寫出文字說明,證明過程或演算步驟。
15.(本小題滿分14分)
設集合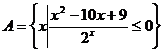
 ,若
,若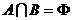 ,求實數
,求實數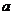 的取值范圍.
的取值范圍.
16..(本小題滿分14分)
已知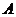 、
、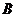 、
、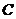 三點的坐標分別為
三點的坐標分別為 、
、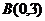 、
、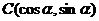 ,
,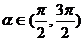 ,
,
(1)若 ,求角
,求角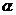 的值;
的值;
(2)若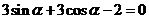 ,求
,求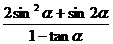 的值。
的值。
17.(本小題滿分14分)
已知函數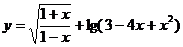 的定義域為
的定義域為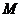 ,當
,當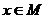 時,
時,
求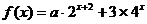
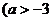 )的最小值。
)的最小值。
18.(本小題滿分14分)
已知數列 的前
的前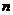 項和為
項和為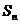 ,若
,若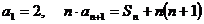 ,
,
(1)求數列 的通項公式;
的通項公式;
(2)令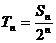 ,問數列
,問數列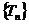 是否有最大的項,若存在則求出最大項的值;若不存在則說明理由。
是否有最大的項,若存在則求出最大項的值;若不存在則說明理由。
19.(本小題滿分14分)
已知函數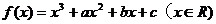 在
在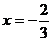 處取得極值,其圖象在點
處取得極值,其圖象在點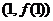 處的切線與直線
處的切線與直線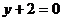 平行
平行
(1)求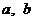 的值;
的值;
(2)若對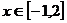 都有
都有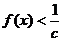 恒成立,求
恒成立,求 的取值范圍。
的取值范圍。

 20.(本小題滿分14分)
20.(本小題滿分14分)
已知二次函數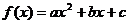 和一次函數
和一次函數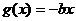 其中
其中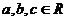 且
且
滿足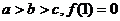 .
.
(1)證明:函數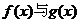 的圖象交于不同的兩點A,B;
的圖象交于不同的兩點A,B;
(2)若函數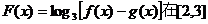 上的最小值為2,最大值為3,求
上的最小值為2,最大值為3,求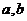 值;
值;
(3)求線段AB在 軸上的射影A1B1的長的取值范圍.
軸上的射影A1B1的長的取值范圍.
一、選擇題:(本題每小題5分,共50分)
1
2
3
4
5
6
7
8
9
10
D
B
C
D
D
C
B
A
A
C
二、填空題:(本題每小題4分,共16分)
11. 12.
12. 13.
13. 14.
14.
三、解答題(本大題6小題,共84分。解答應寫出文字說明,證明過程或演算步驟)
15.(本小題滿分14分)
解 得
得 …………………4分
…………………4分
又

∵
 +1>
+1> 得B={y|y<
得B={y|y< 或y>
或y>
 +1}……………………8分
+1}……………………8分
∵A∩B=φ
 ∴
∴ 
 1
1

 +1
+1 9…………………12分
9…………………12分
∴
 -2
-2 …………………14分
…………………14分
16.(本小題滿分14分)
解:(1) ,
,
由 得
得 又
又
 ………6分
………6分
(2)因

 ………8分
………8分
又 ,
, ,則
,則
即 …………………10分
…………………10分

 …14分
…14分
17.(本小題滿分14分)
解: (…………………3分)
(…………………3分)
 =
= (…………………7分)
(…………………7分)
又 ,
, ,
,
(1)若 ,即
,即 時,
時, =
= =
= ,(…………10分)
,(…………10分)
(2)若 ,即
,即
 時,
時,
所以當 即
即 時,
時, =
= (…………………13分)
(…………………13分)
 (…………………14分)
(…………………14分)
18.(本小題滿分14分)
解:(1)令 ,
, ,即
,即
由

∵ ,∴
,∴ ,即數列
,即數列 是以
是以 為首項、
為首項、 為公差的等差數列, ∴
為公差的等差數列, ∴ …………8分
…………8分
(2) 化簡得
化簡得 ,即
,即
∵ ,又∵
,又∵ 時,
時, …………12分
…………12分
∴各項中最大項的值為 …………14分
…………14分
19.(本小題滿分14分)
解:(1) ,由題意
,由題意 ―――①
―――①
又 ―――②
―――②
聯立得 …………5分
…………5分
(2)依題意得 即
即 ,對
,對 恒成立,設
恒成立,設 ,則
,則
解 得
得
當  ……10分
……10分
則
又 ,所以
,所以 ;故只須
;故只須  …………12分
…………12分
解得
即 的取值范圍是
的取值范圍是 …………14分
…………14分
20.(本小題滿分14分)
解:(1)由 ,
,
 即函數
即函數 的圖象交于不同的兩點A,B; ……4分(2)
的圖象交于不同的兩點A,B; ……4分(2)
已知函數 ,
, 的對稱軸為
的對稱軸為 ,
,
故 在[2,3]上為增函數,
……………6分
在[2,3]上為增函數,
……………6分
 ……8分
……8分
(3)設方程
 ……10分
……10分
 ……12分
……12分
設 的對稱軸為
的對稱軸為 上是減函數,
上是減函數, ……14分
……14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com