
2007年寧波市高三模擬試卷
(數學理科)
說明:本試卷分第Ⅰ卷(選擇題)和第Ⅱ卷(非選擇題)兩部分,共150分.
考試時間120分鐘.
第Ⅰ卷(選擇題 共50分)
一、選擇題:本大題共10小題,每小題5分,共50分.在每小題給出的四個選項中只有一項是符合題目要求的.
1、若全集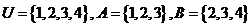 ,則
,則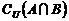 為
為
A.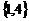 B.
B. C.
C.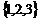 D.
D.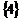
2、復數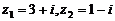 ,則
,則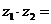
A.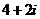 B.
B.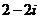 C.
C.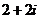 D.
D.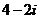
3、下列函數中,是周期函數且在區間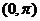 上遞減的是
上遞減的是
A.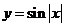 B.
B.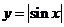 C.
C.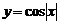 D.
D.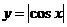
4、已知隨機變量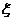 服從正態分布
服從正態分布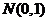 ,若
,若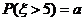 ,則
,則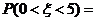
A.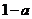 B.
B.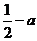 C.
C.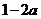 D.
D. 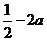
5、“升級”是一種常見的網絡游戲.在游戲的發牌過程中,先從洗好的兩副撲克牌(108張)
中任意抽出8張作為“底牌”,再把剩下的100張牌按確定的順序發牌,每個玩家25張.
這其實是兩個抽樣的過程,其抽樣方法分別是
A.簡單隨機抽樣,分層抽樣 B. 分層抽樣,系統抽樣
C.系統抽樣,分層抽樣 D.簡單隨機抽樣,系統抽樣
6、給出以下四個命題:
①過直線外一點作該直線的垂線是唯一的;
②過直線外一點作該直線的平行平面是唯一的;
③過平面外一點作該平面的垂直平面是唯一的;
④過平面的斜線作該平面的垂直平面是唯一的.
其中真命題的個數為
A.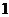 B.
B.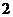 C.
C.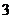 D.
D.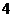
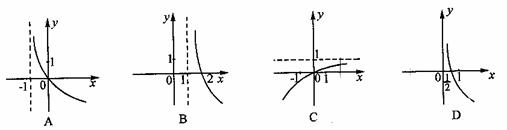
7、已知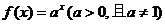 ,
,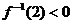 ,則函數
,則函數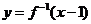 的圖象是
的圖象是
8、在等差數列 中,
中, ,記
,記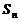 為其前
為其前 項和,則
項和,則
A.
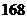 B.
B. C.
C. D.
D.
9、若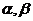 為銳角,則“
為銳角,則“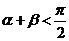 ”是“
”是“ ”的
”的
A.充分非必要條件 B.必要非充分條件
C.充要條件 D.既非充分又非必要條件
10、若集合 、
、 滿足
滿足 ,則稱
,則稱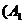 ,
,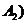 為集合
為集合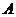 的一個分拆,并規定:當且
的一個分拆,并規定:當且
僅當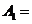
 時,
時,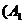 ,
,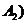 與
與 ,
, 為集合
為集合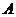 的同一種分拆,則集合
的同一種分拆,則集合
的不同分拆種數是
A. 8 B. 9 C. 26 D. 27
第Ⅱ卷(非選擇題 共100分)
二、填空題:本大題7小題,每小題4分,共28分.把答案填在答案卡中的相應橫線上.
11、橢圓 的兩條準線間的距離是 ▲ .
的兩條準線間的距離是 ▲ .
12、 ▲ .
▲ .
13、在 的展開式中,
的展開式中,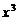 項的系數為 ▲ .
項的系數為 ▲ .
14、 的三內角
的三內角 所對的長分別為
所對的長分別為 ,若向量
,若向量
與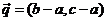 是共線向量, 則角
是共線向量, 則角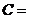 ▲ .
▲ .
15、已知實數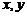 滿足條件
滿足條件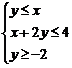 ,則表達式
,則表達式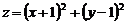 的
的
最小值是 ▲ .
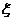
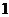
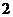
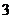
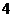
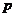
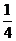
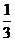
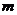
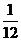
 16、若隨機變量
16、若隨機變量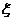 的分布列如表所示,則隨機變量
的分布列如表所示,則隨機變量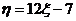 的數學期望是 ▲ .
的數學期望是 ▲ .
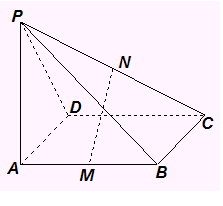
17、如圖、在正三棱錐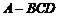 中,
中, 分別是
分別是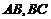 的
的
中點,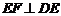 ,且
,且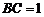 ,則正三棱錐
,則正三棱錐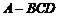 的
的
外接球的面積等于 ▲ .
三、解答題:本大題5小題,其中第18題~第21題每題14分,第22題為16分 ,共72分. 解答應寫出文字說明,證明過程或演算步驟.
 18、四棱錐
18、四棱錐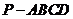 中,
中,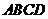 是矩形,
是矩形,
 面
面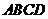 ,
, 分別是
分別是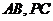 的中點.
的中點.
(1)證明: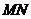 ∥平面
∥平面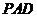 ;
;
(2)若二面角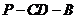 的大小為
的大小為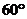 ,
,
求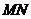 與平面
與平面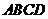 所成的角.
所成的角.
19、函數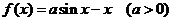 .
.
(1)若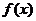 的導函數
的導函數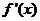 的圖像按向量
的圖像按向量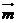 平移后可得到函數
平移后可得到函數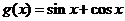 的
的
圖像,求實數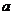 的值;
的值;
(2)當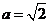 時,求函數
時,求函數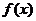 在區間
在區間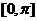 上的最大值和最小值.
上的最大值和最小值.
20、已知函數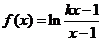 (
(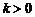 ).
).
(1)求函數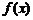 的定義域;
的定義域;
(2)若函數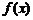 在區間
在區間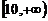 上是增函數,求實數
上是增函數,求實數 的取值范圍.
的取值范圍.
21、已知曲線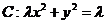
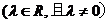 .
.
(1)由曲線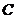 上任一點
上任一點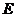 向
向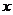 軸作垂線,垂足為
軸作垂線,垂足為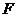 ,點
,點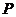 分
分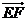 所成的比為
所成的比為 ,
,
問:點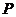 的軌跡可能是圓嗎?請說明理由;
的軌跡可能是圓嗎?請說明理由;
(2)如果直線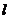 的一個方向向量為
的一個方向向量為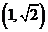 ,且過點
,且過點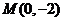 ,直線
,直線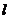 交曲線
交曲線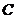 于
于
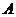 、
、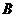 兩點,又
兩點,又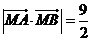 ,求曲線
,求曲線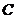 的方程.
的方程.
22、設數列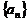 的各項都是正數,且對任意
的各項都是正數,且對任意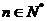 ,都有
,都有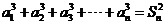 ,
,
其中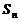 為數列
為數列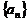 的前
的前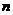 項和.
項和.
(1)求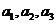 ,并求數列
,并求數列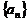 的通項公式;
的通項公式;
(2)設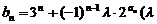 為非零整數,
為非零整數,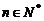 ),試確定
),試確定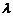 的值,
的值,
使得對任意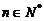 ,都有
,都有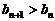 成立.
成立.
一、選擇題:本大題共10小題,每小題5分,共50分.
題號
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
B
D
A
B
B
C
D
二、填空題:本大題7小題,每小題4分,共28分.
11、 ; 12、
; 12、  ; 13、
; 13、 ; 14、
; 14、 ; 15、
; 15、 ; 16、
; 16、 ;17、
;17、 。
。
三、解答題
18、(1)略 ……………………………………………………………………(7分)
(2) 就是二面角
就是二面角 的平面角,即
的平面角,即 ,
,
 …………………………………………………………………(9分)
…………………………………………………………………(9分)
取 中點
中點 ,則
,則 平面
平面 ,
,
 就是
就是 與平面
與平面 所成的角。 …………………………(11分)
所成的角。 …………………………(11分)
 ,
, ,
,
所以 與平面
與平面 所成的角的大小為
所成的角的大小為 。 …………………………(14分)
。 …………………………(14分)
(用向量方法,相應給分)
19、(1) ,
, ,
, …………(7分)
…………(7分)
(2) ,當
,當 時,
時, ;當
;當 時,
時,
 ,而
,而 ,
,
 ……………………………………………(14分)
……………………………………………(14分)
20、(1)當 ,當k=1時,
,當k=1時,
 ……………………………………… (7分)
……………………………………… (7分)
(2)由已知 ,又設
,又設 ,則
,則
 ,
,
知當 時,
時, 為增函數,則知
為增函數,則知 為增函數。…………………(14分)
為增函數。…………………(14分)
(用導數法相應給分)
21、.解:(1)、設 ,則
,則 ,
,
∵點P分 所成的比為
所成的比為 ∴
∴  ∴
∴ 
∴ 代入
代入 中,得
中,得 為P點的軌跡方程.
為P點的軌跡方程.
當 時,軌跡是圓. …………………………………………………(7分)
時,軌跡是圓. …………………………………………………(7分)
(2)、由題設知直線l的方程為 , 設
, 設
聯立方程組 ,消去
,消去 得:
得:
∵ 方程組有兩解 ∴  且
且 ∴
∴ 或
或 且
且
∵
 ∴
∴
又 ∵  ∴
∴  解得
解得 (舍去)或
(舍去)或
∴ 曲線C的方程是 ……………………………………………(14分)
……………………………………………(14分)
22、解(1) ………………………………………………(5分)
………………………………………………(5分)
猜想  , …………………………………………………………(7分)
, …………………………………………………………(7分)
證明(略) ……………………………………………………………………(10分)
(2) ,要使
,要使 恒成立,
恒成立,
 恒成立
恒成立
即 恒成立.
恒成立.
(i)當 為奇數時,即
為奇數時,即 恒成立, 又
恒成立, 又 的最小值為1,
的最小值為1,
(ii)當 為偶數時,即
為偶數時,即 恒成立, 又
恒成立, 又 的最大值為
的最大值為 ,
,
 即
即 ,又
,又 ,
, 為整數,
為整數,
∴ ,使得對任意
,使得對任意 ,都有
,都有 …………………………………( 16分)
…………………………………( 16分)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com