国产日韩欧美一线二线,美女好全身无遮掩免费网战,亚洲欧美另类卡通乱,日韩av日日夜夜澡,女生抽打女生大骚逼,国产精品99久久…,五月婷婷六月丁香亚洲天堂,中文无码精品一区二区三,日本日p视频免费在线观看

設橢圓的左、右頂點分別為，點在橢圓上且異于兩點，為坐標原點.

（Ⅰ）若直線與的斜率之積為，求橢圓的離心率；

（Ⅱ）若，證明直線的斜率 滿足

【解析】(1)解：設點P的坐標為.由題意，有  ①

由，得，

由，可得，代入①并整理得

由于，故.于是，所以橢圓的離心率

（2）證明：（方法一）

依題意，直線OP的方程為，設點P的坐標為.

由條件得消去并整理得  ②

由，及，

得.

整理得.而，于是，代入②，

整理得

由，故，因此.

所以.

(方法二)

依題意，直線OP的方程為，設點P的坐標為.

由P在橢圓上，有

因為，，所以，即   ③

由，，得整理得.

于是，代入③，

整理得

解得，

所以.

 

已知，函數

（1）當時，求函數在點(1，)的切線方程；

(2)求函數在[－1，1]的極值；

(3)若在上至少存在一個實數x₀，使>g(x_o)成立，求正實數的取值范圍。

【解析】本試題中導數在研究函數中的運用。（1）中，那么當時，  又    所以函數在點(1，)的切線方程為；（2）中令   有 

對a分類討論，和得到極值。（3）中，設，，依題意，只需那么可以解得。

解：（Ⅰ）∵  ∴

∴  當時，  又    

∴  函數在點(1，)的切線方程為 --------4分

（Ⅱ）令   有 

①         當即時

	（－1，0）	0	（0，）		（，1）
	+	0	－	0	+
		極大值		極小值

故的極大值是，極小值是

②         當即時，在（－1,0）上遞增，在（0,1）上遞減，則的極大值為，無極小值。 

綜上所述   時，極大值為，無極小值

時  極大值是，極小值是        ----------8分

（Ⅲ）設，

對求導，得

∵，    

∴ 在區間上為增函數，則

依題意，只需，即 

解得  或（舍去）

則正實數的取值范圍是（，）

 

現有4個人去參加某娛樂活動，該活動有甲、乙兩個游戲可供參加者選擇.為增加趣味性，約定：每個人通過擲一枚質地均勻的骰子決定自己去參加哪個游戲，擲出點數為1或2的人去參加甲游戲，擲出點數大于2的人去參加乙游戲.

（Ⅰ）求這4個人中恰有2人去參加甲游戲的概率；

（Ⅱ）求這4個人中去參加甲游戲的人數大于去參加乙游戲的人數的概率；

（Ⅲ）用X，Y分別表示這4個人中去參加甲、乙游戲的人數，記，求隨機變量的分布列與數學期望.

【解析】依題意，這4個人中，每個人去參加甲游戲的概率為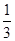，去參加乙游戲的概率為.

設“這4個人中恰有i人去參加甲游戲”為事件

則.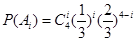

（1）這4個人中恰有2人去參加甲游戲的概率

（2）設“這4個人中去參加甲游戲的人數大于去參加乙游戲的人數”為事件B，則.由于互斥，故

所以，這個人中去參加甲游戲的人數大于去參加乙游戲的人數的概率為.

（3）的所有可能取值為0,2,4.由于互斥，互斥，故

    

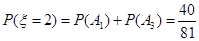
所以的分布列是

	0	2	4
P

隨機變量的數學期望.

 

已知函數，.

（Ⅰ）若函數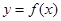依次在處取到極值.求的取值范圍；

（Ⅱ）若存在實數，使對任意的，不等式 恒成立.求正整數的最大值.

【解析】第一問中利用導數在在處取到極值點可知導數為零可以解得方程有三個不同的實數根來分析求解。

第二問中，利用存在實數，使對任意的，不等式 恒成立轉化為，恒成立，分離參數法求解得到范圍。

解：（1）

①

（2）不等式 ，即，即.

轉化為存在實數，使對任意的，不等式恒成立.

即不等式在上恒成立.

即不等式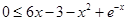在上恒成立.

設，則.

設，則，因為，有.

故在區間上是減函數。又

故存在，使得.

當時，有，當時，有.

從而在區間上遞增，在區間上遞減.

又[來源:]

所以當時，恒有；當時，恒有；

故使命題成立的正整數m的最大值為5