題目列表(包括答案和解析)
（12分）已知拋物線C的頂點在坐標原點O，準線方程是
，過點
的直線
與拋物線C相交于不同的兩點A，B
（I）求拋物線C的方程及直線的斜率
的取值范圍；
（Ⅱ）求
（用表示）
| AB |
已知雙曲線C的中心在坐標原點O，兩條準線的距離為
，其中一個焦點恰與拋物線x 2 + 10 x 4 y + 21 = 0的焦點重合。
（1）求雙曲線C的方程；
（2）若P為C上任意一點，A為雙曲線的右頂點，通過P、O的直線與從A所引平行于漸近線的直線分別交于Q、R。試證明：| OP |是| OQ |與| OR |的等比中項。
如圖，已知拋物線C的頂點在原點O，焦點為F(0，1)．
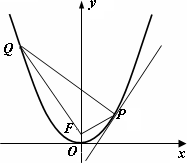
(Ⅰ)求拋物線C的方程；
(Ⅱ)在拋物線C上是否存在點P，使得過點P的直線交拋物線C于另一點Q，滿足PF⊥QP，且PQ與拋物線C在點P處的切線垂直？若存在，求出點P的坐標；若不存在，請說明理由．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| a2+b2 |
一、選擇題：（每小題5分，共50分）
題號
1
2
3
4
5
6
7
8
9
10
答案
B
D
B
A
C
C
D
A
A
B
二、填空題：（每小題4分，共24分）
11．
； 12．
； 13．
； 14．
； 15．4 16．120
三、解答題：（共76分，以下各題為累計得分，其他解法請相應給分）
17．解：（I）
由
，得
。
又當
時
，得
（Ⅱ）當
即
時函數遞增。
故
的單調增區間為
，
又由
，得
，
由
解得
故使
成立的
的集合是
18．解：（I）設袋中有白球個，由題意得
，
即
解得
或
（舍），故有白球6個
（法二，設黑球有個，則全是黑球的概率為
由
即
，解得
或
（舍），故有黑球4個，白球6個
（Ⅱ）
，
0
1
2
3
P
故分布列為
數學期望
19．解：（I）取AB的中點O，連接OP，OC
PA=PB 
PO
AB
又在
中，
，
在
中，
，又
，故有
又
，
面ABC
又PO
面PAB，面PAB面ABC
（Ⅱ）以O為坐標原點，
分別以OB，OC，OP為軸，
軸，
軸建立坐標系，
如圖，則A
設平面PAC的一個法向量為
。
得
令
，則
設直線PB與平面PAC所成角為
于是
20．解：（I）由題意設C的方程為
由
，得
。
設直線
的方程為
，由
②代入①化簡整理得 
因直線與拋物線C相交于不同的兩點，
故
即
，解得
又
時僅交一點，
（Ⅱ）設
，由由（I）知
21．解：（I）當
時，
設曲線
與
在公共點（
）處的切線相同，則有
即
解得
或
（舍）
又
故得
公共點為
，
切線方程為 
，即
（Ⅱ）
，設在（
）處切線相同，
故有
即
由①
，得
（舍）
于是
令
，則
于是當
即
時，
，故
在
上遞增。
當
，即
時，
，故在
上遞減
在
處取最大值。
當
時，b取得最大值
22．解：（I）
的對稱軸為
，又當
時，
，
故
在[0，1]上是增函數
即
（Ⅱ）
由
得
①―②得
即
當
時，
，當
時，
于是
設存在正整數
，使對，
恒成立。
當時，
，即
當時，
。
當
時，
，當
時，
，當
時，
存在正整數
或8，對于任意正整數
都有成立。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com