
題目列表(包括答案和解析)
如圖所示的長方體 中,底面
中,底面 是邊長為
是邊長為 的正方形,
的正方形, 為
為 與
與 的交點,
的交點, ,
, 是線段
是線段 的中點.
的中點.
(Ⅰ)求證: 平面
平面 ;
;
(Ⅱ)求證: 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
【解析】本試題主要考查了線面平行的判定定理和線面垂直的判定定理,以及二面角的求解的運用。中利用 ,又
,又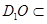 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 由
由 ,
, ,又
,又 ,∴
,∴ 平面
平面 .
可得證明
.
可得證明
(3)因為∴ 為面
為面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 為平面
為平面 的法向量.∴利用法向量的夾角公式,
的法向量.∴利用法向量的夾角公式, ,
,
∴ 與
與 的夾角為
的夾角為 ,即二面角
,即二面角 的大小為
的大小為 .
.
方法一:解:(Ⅰ)建立如圖所示的空間直角坐標系.連接 ,則點
,則點 、
、 ,
,

∴ ,又點
,又點 ,
, ,∴
,∴
∴ ,且
,且 與
與 不共線,∴
不共線,∴ .
.
又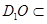 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 .…………………4分
.…………………4分
(Ⅱ)∵ ,
,
∴ ,
, ,即
,即 ,
, ,
,
又 ,∴
,∴ 平面
平面 . ………8分
. ………8分
(Ⅲ)∵ ,
, ,∴
,∴ 平面
平面 ,
,
∴ 為面
為面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 為平面
為平面 的法向量.∴
的法向量.∴ ,
,
∴ 與
與 的夾角為
的夾角為 ,即二面角
,即二面角 的大小為
的大小為
已知 是等差數列,其前n項和為Sn,
是等差數列,其前n項和為Sn, 是等比數列,且
是等比數列,且 ,
, .
.
(Ⅰ)求數列 與
與 的通項公式;
的通項公式;
(Ⅱ)記 ,
, ,證明
,證明 (
( ).
).
【解析】(1)設等差數列 的公差為d,等比數列
的公差為d,等比數列 的公比為q.
的公比為q.
由 ,得
,得 ,
, ,
, .
.
由條件,得方程組 ,解得
,解得
所以 ,
, ,
, .
.
(2)證明:(方法一)
由(1)得
 ①
①
 ②
②
由②-①得



而
故 ,
,
(方法二:數學歸納法)
① 當n=1時,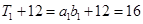 ,
, ,故等式成立.
,故等式成立.
② 假設當n=k時等式成立,即 ,則當n=k+1時,有:
,則當n=k+1時,有:






即 ,因此n=k+1時等式也成立
,因此n=k+1時等式也成立
由①和②,可知對任意 ,
, 成立.
成立.
已知向量 (
( ),向量
),向量 ,
, ,
,
且

 .
.
(Ⅰ)求向量 ;
(Ⅱ)若
;
(Ⅱ)若 ,
, ,求
,求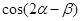 .
.
【解析】本試題主要考查了向量的數量積的運算,以及兩角和差的三角函數關系式的運用。
(1)問中∵ ,∴
,∴ ,…………………1分
,…………………1分
∵ ,得到三角關系是
,得到三角關系是 ,結合
,結合 ,解得。
,解得。
(2)由 ,解得
,解得 ,
, ,結合二倍角公式
,結合二倍角公式 ,和
,和 ,代入到兩角和的三角函數關系式中就可以求解得到。
,代入到兩角和的三角函數關系式中就可以求解得到。
解析一:(Ⅰ)∵ ,∴
,∴ ,…………1分
,…………1分
∵ ,∴
,∴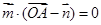 ,即
,即 ① …………2分
① …………2分
又 ② 由①②聯立方程解得,
② 由①②聯立方程解得,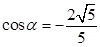 ,
,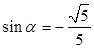 5分
5分
∴ ……………6分
……………6分
(Ⅱ)∵ 即
即 ,
, , …………7分
, …………7分
∴ ,
, ………8分
………8分
又∵ , ………9分
, ………9分
 , ……10分
, ……10分
∴ .
.
解法二: (Ⅰ) ,…………………………………1分
,…………………………………1分
又 ,∴
,∴ ,即
,即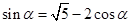 ,①……2分
,①……2分
又 ②
②
將①代入②中,可得 ③ …………………4分
③ …………………4分
將③代入①中,得 ……………………………………5分
……………………………………5分
∴ …………………………………6分
…………………………………6分
(Ⅱ) 方法一
∵ ,
, ,∴
,∴ ,且
,且 ……7分
……7分
∴ ,從而
,從而 . …………………8分
. …………………8分
由(Ⅰ)知 ,
,
 ; ………………9分
; ………………9分
∴ . ………………………………10分
. ………………………………10分
又∵ ,∴
,∴ ,
又
,
又 ,∴
,∴ ……11分
……11分
綜上可得  ………………………………12分
………………………………12分
方法二∵ ,
, ,∴
,∴ ,且
,且 …………7分
…………7分
∴ .
……………8分
.
……………8分
由(Ⅰ)知 ,
, .
…………9分
.
…………9分
∴ ……………10分
……………10分
∵ ,且注意到
,且注意到 ,
,
∴ ,又
,又 ,∴
,∴ ………………………11分
………………………11分
綜上可得  …………………12分
…………………12分
(若用 ,又∵
,又∵ ∴
∴  ,
,
雙曲線![]() 的一條漸近線為
的一條漸近線為![]() ,由方程組
,由方程組 ,消去y,得
,消去y,得![]() 有唯一解,所以△=
有唯一解,所以△=![]() ,
,
所以![]() ,
,![]() ,故選D. w.w.w.k.s.5.u.c.o.m
,故選D. w.w.w.k.s.5.u.c.o.m ![]()
![]()
答案:D.
【命題立意】:本題考查了雙曲線的漸近線的方程和離心率的概念,以及直線與拋物線的位置關系,只有一個公共點,則解方程組有唯一解.本題較好地考查了基本概念基本方法和基本技能.
設橢圓 的左、右頂點分別為
的左、右頂點分別為 ,點
,點 在橢圓上且異于
在橢圓上且異于 兩點,
兩點, 為坐標原點.
為坐標原點.
(Ⅰ)若直線 與
與 的斜率之積為
的斜率之積為 ,求橢圓的離心率;
,求橢圓的離心率;
(Ⅱ)若 ,證明直線
,證明直線 的斜率
的斜率
 滿足
滿足
【解析】(1)解:設點P的坐標為 .由題意,有
.由題意,有 ①
①
由 ,得
,得 ,
,
由 ,可得
,可得 ,代入①并整理得
,代入①并整理得
由于 ,故
,故 .于是
.于是 ,所以橢圓的離心率
,所以橢圓的離心率
(2)證明:(方法一)
依題意,直線OP的方程為 ,設點P的坐標為
,設點P的坐標為 .
.
由條件得 消去
消去 并整理得
并整理得 ②
②
由 ,
, 及
及 ,
,
得 .
.
整理得 .而
.而 ,于是
,于是 ,代入②,
,代入②,
整理得
由 ,故
,故 ,因此
,因此 .
.
所以 .
.
(方法二)
依題意,直線OP的方程為 ,設點P的坐標為
,設點P的坐標為 .
.
由P在橢圓上,有
因為 ,
, ,所以
,所以 ,即
,即 ③
③
由 ,
, ,得
,得 整理得
整理得 .
.
于是 ,代入③,
,代入③,
整理得
解得 ,
,
所以 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com