
題目列表(包括答案和解析)
 (a>b>0)的一個頂點坐標為A(
(a>b>0)的一個頂點坐標為A(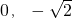 ),且其右焦點到直線
),且其右焦點到直線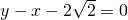 的距離為3.
的距離為3.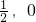 ),求證點M的所有“相關弦”的中點在同一條直線上;
),求證點M的所有“相關弦”的中點在同一條直線上;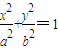 (a>b>0)的一個頂點坐標為A(
(a>b>0)的一個頂點坐標為A(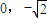 ),且其右焦點到直線
),且其右焦點到直線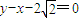 的距離為3.
的距離為3.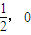 ),求證點M的所有“相關弦”的中點在同一條直線上;
),求證點M的所有“相關弦”的中點在同一條直線上;設橢圓 的左、右頂點分別為
的左、右頂點分別為 ,點
,點 在橢圓上且異于
在橢圓上且異于 兩點,
兩點, 為坐標原點.
為坐標原點.
(Ⅰ)若直線 與
與 的斜率之積為
的斜率之積為 ,求橢圓的離心率;
,求橢圓的離心率;
(Ⅱ)若 ,證明直線
,證明直線 的斜率
的斜率
 滿足
滿足
【解析】(1)解:設點P的坐標為 .由題意,有
.由題意,有 ①
①
由 ,得
,得 ,
,
由 ,可得
,可得 ,代入①并整理得
,代入①并整理得
由于 ,故
,故 .于是
.于是 ,所以橢圓的離心率
,所以橢圓的離心率
(2)證明:(方法一)
依題意,直線OP的方程為 ,設點P的坐標為
,設點P的坐標為 .
.
由條件得 消去
消去 并整理得
并整理得 ②
②
由 ,
, 及
及 ,
,
得 .
.
整理得 .而
.而 ,于是
,于是 ,代入②,
,代入②,
整理得
由 ,故
,故 ,因此
,因此 .
.
所以 .
.
(方法二)
依題意,直線OP的方程為 ,設點P的坐標為
,設點P的坐標為 .
.
由P在橢圓上,有
因為 ,
, ,所以
,所以 ,即
,即 ③
③
由 ,
, ,得
,得 整理得
整理得 .
.
于是 ,代入③,
,代入③,
整理得
解得 ,
,
所以 .
.
設橢圓 (常數
(常數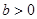 )的左右焦點分別為
)的左右焦點分別為 ,
, 是直線
是直線 上的兩個動點,
上的兩個動點, .
.
(1)若 ,求
,求 的值;
的值;
(2)求 的最小值.
的最小值.

【解析】第一問中解:設 ,
, 則
則
由 得
得 由
由 ,得
,得
 ②
②

第二問易求橢圓 的標準方程為:
的標準方程為:
 ,
,
所以,當且僅當 或
或 時,
時, 取最小值
取最小值 .
.
解:設 ,
, ……………………1分
……………………1分
則 ,由
,由 得
得 ①……2分
①……2分
(1)由 ,得
,得 ② ……………1分
② ……………1分
 ③ ………………………1分
③ ………………………1分
由①、②、③三式,消去 ,并求得
,并求得 .
………………………3分
.
………………………3分
(2)解法一:易求橢圓 的標準方程為:
的標準方程為: .………………2分
.………………2分
 , ……4分
, ……4分
所以,當且僅當 或
或 時,
時, 取最小值
取最小值 .…2分
.…2分
解法二: ,
………………4分
,
………………4分
所以,當且僅當 或
或 時,
時, 取最小值
取最小值
|
| OB |
| OA |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com