
【題目】給出如下四個命題:①若“p且![]() ”為假命題,則p、q均為假命題;②命題“若a>b,則
”為假命題,則p、q均為假命題;②命題“若a>b,則![]() ”的否命題為“若a≤b,則
”的否命題為“若a≤b,則![]() ”;③“x∈R,
”;③“x∈R,![]() 的否定是“
的否定是“![]() ”;④在△ABC中,“A>B”是“
”;④在△ABC中,“A>B”是“![]() ”的充要條件;其中正確的命題的個數(shù)是( )
”的充要條件;其中正確的命題的個數(shù)是( )
A.1B.2C.3D.4
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 過點
過點![]() ,該拋物線的準(zhǔn)線與橢圓
,該拋物線的準(zhǔn)線與橢圓![]() :
:![]() 相切,且橢圓的離心率為
相切,且橢圓的離心率為![]() ,點
,點![]() 為橢圓
為橢圓![]() 的右焦點.
的右焦點.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]()
![]() 兩點,
兩點,![]() 為平面上一定點,且滿足
為平面上一定點,且滿足![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】海面上漂浮著![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 七個島嶼,島與島之間都沒有橋連接,小昊住在
七個島嶼,島與島之間都沒有橋連接,小昊住在![]() 島,小皓住在
島,小皓住在![]() 島.現(xiàn)政府計劃在這七個島之間建造
島.現(xiàn)政府計劃在這七個島之間建造![]() 座橋(每兩個島之間至多建造一座橋).若
座橋(每兩個島之間至多建造一座橋).若![]() ,則橋建完后,小吳和小皓可以往來的概率為______;若
,則橋建完后,小吳和小皓可以往來的概率為______;若![]() ,則橋建完后,小昊和小皓可以往來的概率為______.
,則橋建完后,小昊和小皓可以往來的概率為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某同學(xué)理科成績優(yōu)異,今年參加了數(shù)學(xué),物理,化學(xué),生物4門學(xué)科競賽.已知該同學(xué)數(shù)學(xué)獲一等獎的概率為![]() ,物理,化學(xué),生物獲一等獎的概率都是
,物理,化學(xué),生物獲一等獎的概率都是![]() ,且四門學(xué)科是否獲一等獎相互獨立.
,且四門學(xué)科是否獲一等獎相互獨立.
(1)求該同學(xué)至多有一門學(xué)科獲得一等獎的概率;
(2)用隨機變量![]() 表示該同學(xué)獲得一等獎的總數(shù),求
表示該同學(xué)獲得一等獎的總數(shù),求![]() 的概率分布和數(shù)學(xué)期望
的概率分布和數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知長方形![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點. 將
的中點. 將![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
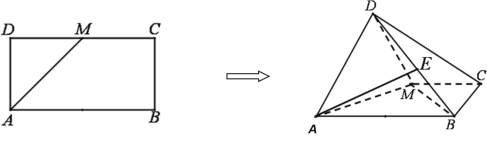
(1)求證:![]() .
.
(2)點![]() 是線段
是線段![]() 上的一動點,當(dāng)二面角
上的一動點,當(dāng)二面角![]() 大小為
大小為![]() 時,試確定點
時,試確定點![]() 的位置.
的位置.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
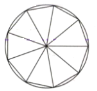
【題目】劉徽(約公元225年-295年),魏晉期間偉大的數(shù)學(xué)家,中國古典數(shù)學(xué)理論的奠基人之一他在割圓術(shù)中提出的,“割之彌細(xì),所失彌少,割之又割,以至于不可割,則與圓周合體而無所失矣”,這可視為中國古代極限觀念的佳作,割圓術(shù)的核心思想是將一個圓的內(nèi)接正n邊形等分成n個等腰三角形(如圖所示),當(dāng)n變得很大時,這n個等腰三角形的面積之和近似等于圓的面積,運用割圓術(shù)的思想,得到![]() 的近似值為( )
的近似值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,點
,點![]() 是拋物線
是拋物線![]() 上任意一點,以
上任意一點,以![]() 為直徑作圓
為直徑作圓![]() .
.
(1)判斷圓![]() 與坐標(biāo)
與坐標(biāo)![]() 軸的位置關(guān)系,并證明你的結(jié)論;
軸的位置關(guān)系,并證明你的結(jié)論;
(2)設(shè)直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() ,且
,且![]() ,若
,若![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了調(diào)查某廠工人生產(chǎn)某件產(chǎn)品的效率,隨機抽查了100名工人某天生產(chǎn)該產(chǎn)品的數(shù)量,所取樣本數(shù)據(jù)分組區(qū)間為![]() ,
,![]() 由此得到如圖所示頻率分布直方圖.
由此得到如圖所示頻率分布直方圖.
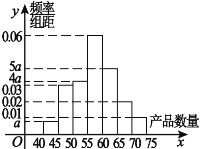
(1)求![]() 的值并估計該廠工人一天生產(chǎn)此產(chǎn)品數(shù)量的平均值;
的值并估計該廠工人一天生產(chǎn)此產(chǎn)品數(shù)量的平均值;
(2)從生產(chǎn)產(chǎn)品數(shù)量在![]() 的四組工人中,用分層抽樣方法抽取13人,則每層各應(yīng)抽取多少人?
的四組工人中,用分層抽樣方法抽取13人,則每層各應(yīng)抽取多少人?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com