
【題目】已知橢圓![]() 的中心在原點,對稱軸為坐標軸,橢圓
的中心在原點,對稱軸為坐標軸,橢圓![]() 與直線
與直線![]() 相切于點
相切于點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() :
: ![]() 與橢圓相交于
與橢圓相交于![]() 、
、![]() 兩點(
兩點(![]() ,
, ![]() 不是長軸端點),且以
不是長軸端點),且以![]() 為直徑的圓過橢圓
為直徑的圓過橢圓![]() 在
在![]() 軸正半軸上的頂點,求證:直線過定點,并求出該定點的坐標.
軸正半軸上的頂點,求證:直線過定點,并求出該定點的坐標.
【答案】(1) ![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】試題分析:(1)利用點在橢圓上及相切關系布列方程組,即可解得橢圓![]() 的標準方程;
的標準方程;
(2)聯立方程易得: ![]() ,
, ![]() ,以
,以![]() 為直徑的圓過橢圓
為直徑的圓過橢圓![]() 在
在![]() 軸正半軸上的頂點,∴
軸正半軸上的頂點,∴![]() ,即
,即![]() 或
或![]() ,經檢驗得到結果.
,經檢驗得到結果.
試題解析:
法一(Ⅰ)由題意設橢圓的標準方程為![]() (
(![]() ,
, ![]() 且
且![]() )
)
∵![]() 在橢圓上,∴
在橢圓上,∴![]() ①
①
由 得
得![]()
∵橢圓![]() 與直線
與直線![]() 相切,∴
相切,∴![]() ,
,
即![]() ②
②
由①②知![]() ,
, ![]()
故所求橢圓方程為![]()
法二:設橢圓為![]() (
(![]() ,
, ![]() 且
且![]() )則它在點
)則它在點![]() 處的切線為
處的切線為 ,它與
,它與![]() 表示同一直線,∴
表示同一直線,∴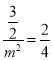 ,
, ![]() ,∴
,∴![]() ,
, ![]()
故所求橢圓方程為![]() .
.
(Ⅱ)設![]() ,
, ![]() ,聯立
,聯立
得![]()
![]() 得
得![]()
![]() ,
, ![]()
![]() ,
,
因為以![]() 為直徑的圓過橢圓的上頂點
為直徑的圓過橢圓的上頂點![]()
∴![]() 即
即![]()
∴![]()
即![]()
即![]()
即![]()
∴![]() 或
或![]()
當![]() 時,直線
時,直線![]() 過定點
過定點![]() 與已知矛盾
與已知矛盾
當![]() 時,直線
時,直線![]() 過定點
過定點![]() 滿足
滿足![]()
所以,直線![]() 過定點,定點坐標為
過定點,定點坐標為![]()


 小學數學口算題卡脫口而出系列答案
小學數學口算題卡脫口而出系列答案 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案科目:高中數學 來源: 題型:
【題目】(2016·北京卷)如圖,在四棱錐P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=![]() .
.
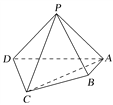
(1)求證:PD⊥平面PAB;
(2)求直線PB與平面PCD所成角的正弦值;
(3)在棱PA上是否存在點M,使得BM∥平面PCD?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0),四點P1(1,1),P2(0,1),P3(–1,
(a>b>0),四點P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三點在橢圓C上.
)中恰有三點在橢圓C上.
(1)求C的方程;
(2)設直線l不經過P2點且與C相交于A,B兩點.若直線P2A與直線P2B的斜率的和為–1,證明:l過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() .
.
(1)求圓心C的坐標及半徑r的大小;
(2)已知不過原點的直線l與圓C相切,且在x軸、y軸上的截距相等,求直線l的方程;
(3)從圓外一點![]() 向圓引一條切線,切點為M,O為坐標原點,且
向圓引一條切線,切點為M,O為坐標原點,且![]() ,求點P的軌跡方程.
,求點P的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】廟會是我國古老的傳統民俗文化活動,又稱“廟市”或 “節場”.廟會大多在春節、元宵節等節日舉行.廟會上有豐富多彩的文化娛樂活動,如“砸金蛋”(游玩者每次砸碎一顆金蛋,如果有獎品,則“中獎”).今年春節期間,某校甲、乙、丙、丁四位同學相約來到某廟會,每人均獲得砸一顆金蛋的機會.游戲開始前,甲、乙、丙、丁四位同學對游戲中獎結果進行了預測,預測結果如下:
甲說:“我或乙能中獎”; 乙說:“丁能中獎”;
丙說:“我或乙能中獎”; 丁說:“甲不能中獎”.
游戲結束后,這四位同學中只有一位同學中獎,且只有一位同學的預測結果是正確的,則中獎的同學是( )

A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于![]() 若數列
若數列![]() 滿足
滿足![]() 則稱這個數列為“
則稱這個數列為“![]() 數列”.
數列”.
(Ⅰ)已知數列1, ![]() 是“
是“![]() 數列”,求實數
數列”,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)是否存在首項為![]() 的等差數列
的等差數列![]() 為“
為“![]() 數列”,且其前
數列”,且其前![]() 項和
項和![]() 使得
使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的通項公式;若不存在,請說明理由;
的通項公式;若不存在,請說明理由;
(Ⅲ)已知各項均為正整數的等比數列![]() 是“
是“![]() 數列”,數列
數列”,數列![]() 不是“
不是“![]() 數列”,若
數列”,若![]() 試判斷數列
試判斷數列![]() 是否為“
是否為“![]() 數列”,并說明理由.
數列”,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com