
【題目】已知函數(shù)f(x)=(x﹣2)ex﹣ ![]() +kx(k是常數(shù),e是自然對數(shù)的底數(shù),e=2.71828…)在區(qū)間(0,2)內(nèi)存在兩個極值點,則實數(shù)k的取值范圍是 .
+kx(k是常數(shù),e是自然對數(shù)的底數(shù),e=2.71828…)在區(qū)間(0,2)內(nèi)存在兩個極值點,則實數(shù)k的取值范圍是 .
【答案】(1,e)∪(e,e2)
【解析】解:f′(x)=(x﹣1)ex﹣k(x﹣1)=(x﹣1)(ex﹣k), 若f(x)在(0,2)內(nèi)存在兩個極值點,
則f′(x)=0在(0,2)有2個解,
令f′(x)=0,解得:x=1或k=ex ,
而y=ex(0<x<2)的值域是(1,e2),
故k∈(1,e)∪(e,e2),
所以答案是:(1,e)∪(e,e2).
【考點精析】本題主要考查了函數(shù)的極值與導數(shù)的相關(guān)知識點,需要掌握求函數(shù)![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側(cè)
附近的左側(cè)![]() ,右側(cè)
,右側(cè)![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側(cè)
附近的左側(cè)![]() ,右側(cè)
,右側(cè)![]() ,那么
,那么![]() 是極小值才能正確解答此題.
是極小值才能正確解答此題.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,在矩形 ![]() 中,
中, ![]() ,點
,點 ![]() 為
為 ![]() 的中點,
的中點, ![]() 為線段
為線段 ![]() (端點除外)上一動點.現(xiàn)將
(端點除外)上一動點.現(xiàn)將 ![]() 沿
沿 ![]() 折起,使得平面
折起,使得平面 ![]() 平面
平面 ![]() .設(shè)直線
.設(shè)直線 ![]() 與平面
與平面 ![]() 所成角為
所成角為 ![]() ,則
,則 ![]() 的最大值為( )
的最大值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)y=cosx的圖象與直線x= ![]() ,x=
,x= ![]() 以及x軸所圍成的圖形的面積為a,則(x﹣
以及x軸所圍成的圖形的面積為a,則(x﹣ ![]() )(2x﹣
)(2x﹣ ![]() )5的展開式中的常數(shù)項為(用數(shù)字作答).
)5的展開式中的常數(shù)項為(用數(shù)字作答).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知橢圓C: ![]() 的右頂點為A,離心率為e,且橢圓C過點
的右頂點為A,離心率為e,且橢圓C過點 ![]() ,以AE為直徑的圓恰好經(jīng)過橢圓的右焦點.
,以AE為直徑的圓恰好經(jīng)過橢圓的右焦點.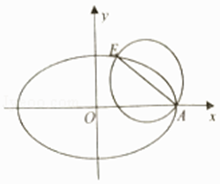
(1)求橢圓C的標準方程;
(2)已知動直線l(直線l不過原點且斜率存在)與橢圓C交于P,Q兩個不同的點,且△OPQ的面積S=1,若N為線段PQ的中點,問:在x軸上是否存在兩個定點E1 , E2 , 使得直線NE1與NE2的斜率之積為定值?若存在,求出E1 , E2的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知MOD函數(shù)是一個求余函數(shù),記MOD(m,n)表示m除以n的余數(shù),例如MOD(8,3)=2.如圖是某個算法的程序框圖,若輸入m的值為48時,則輸出i的值為( ) 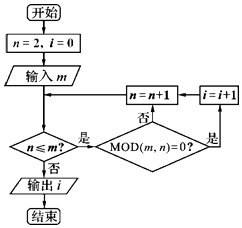
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)![]() 為實數(shù),設(shè)函數(shù)
為實數(shù),設(shè)函數(shù)![]() ,設(shè)
,設(shè)
![]() .
.
(1)求![]() 的取值范圍,并把
的取值范圍,并把![]() 表示為
表示為![]() 的函數(shù)
的函數(shù)![]() ;
;
(2)若![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若存在![]() 使得
使得![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知直線 ![]() 過坐標原點
過坐標原點 ![]() ,圓
,圓 ![]() 的方程為
的方程為 ![]() .
.
(1)當直線 ![]() 的斜率為
的斜率為 ![]() 時,求
時,求 ![]() 與圓
與圓 ![]() 相交所得的弦長;
相交所得的弦長;
(2)設(shè)直線 ![]() 與圓
與圓 ![]() 交于兩點
交于兩點 ![]() ,且
,且 ![]() 為
為 ![]() 的中點,求直線
的中點,求直線 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線 ![]() 的頂點在原點
的頂點在原點 ![]() ,對稱軸是
,對稱軸是 ![]() 軸,且過點
軸,且過點 ![]() .
.
(Ⅰ)求拋物線 ![]() 的方程;
的方程;
(Ⅱ)已知斜率為 ![]() 的直線
的直線 ![]() 交
交 ![]() 軸于點
軸于點 ![]() ,且與曲線
,且與曲線 ![]() 相切于點
相切于點 ![]() ,點
,點 ![]() 在曲線
在曲線 ![]() 上,且直線
上,且直線 ![]() 軸,
軸, ![]() 關(guān)于點
關(guān)于點 ![]() 的對稱點為
的對稱點為 ![]() ,判斷點
,判斷點 ![]() 是否共線,并說明理由.
是否共線,并說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com