
【題目】臺球是一項國際上廣泛流行的高雅室內體育運動,也叫桌球(中國粵港澳地區的叫法)、撞球(中國臺灣地區的叫法)控制撞球點、球的旋轉等控制母球走位是擊球的一項重要技術,一次臺球技術表演節目中,在臺球桌上,畫出如圖正方形ABCD,在點E,F處各放一個目標球,表演者先將母球放在點A處,通過擊打母球,使其依次撞擊點E,F處的目標球,最后停在點C處,若AE=50cm.EF=40cm.FC=30cm,∠AEF=∠CFE=60°,則該正方形的邊長為( )
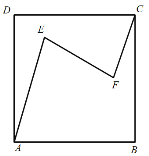
A.50![]() cmB.40
cmB.40![]() cmC.50cmD.20
cmC.50cmD.20![]() cm
cm
 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 是正三角形,
是正三角形,![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 為底面
為底面![]() 內的動點,則下列結論正確的是( )
內的動點,則下列結論正確的是( )

A.若![]() 時,平面
時,平面![]() 平面
平面![]()
B.若![]() 時,直線
時,直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]()
C.若直線![]() 和
和![]() 異面時,點
異面時,點![]() 不可能為底面
不可能為底面![]() 的中心
的中心
D.若平面![]() 平面
平面![]() ,且點
,且點![]() 為底面
為底面![]() 的中心時,
的中心時,![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新高考,取消文理科,實行“![]() ”,成績由語文、數學、外語統一高考成績和自主選考的3門普通高中學業水平考試等級性考試科目成績構成.為了解各年齡層對新高考的了解情況,隨機調查50人(把年齡在
”,成績由語文、數學、外語統一高考成績和自主選考的3門普通高中學業水平考試等級性考試科目成績構成.為了解各年齡層對新高考的了解情況,隨機調查50人(把年齡在![]() 稱為中青年,年齡在
稱為中青年,年齡在![]() 稱為中老年),并把調查結果制成下表:
稱為中老年),并把調查結果制成下表:
年齡(歲) |
|
|
|
|
|
|
頻數 | 5 | 15 | 10 | 10 | 5 | 5 |
了解 | 4 | 12 | 6 | 5 | 2 | 1 |
(1)分別估計中青年和中老年對新高考了解的概率;
(2)請根據上表完成下面![]() 列聯表,是否有95%的把握判斷對新高考的了解與年齡(中青年、中老年)有關?
列聯表,是否有95%的把握判斷對新高考的了解與年齡(中青年、中老年)有關?
了解新高考 | 不了解新高考 | 總計 | |
中青年 | |||
中老年 | |||
總計 |
附: .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(3)若從年齡在![]() 的被調查者中隨機選取3人進行調查,記選中的3人中了解新高考的人數為
的被調查者中隨機選取3人進行調查,記選中的3人中了解新高考的人數為![]() ,求
,求![]() 的分布列以及
的分布列以及![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知圓F1:(x+1)2 +y2= r2(1≤r≤3),圓F2:(x-1)2+y2= (4-r)2.
(1)證明:圓F1與圓F2有公共點,并求公共點的軌跡E的方程;
(2)已知點Q(m,0)(m<0),過點E斜率為k(k≠0)的直線與(Ⅰ)中軌跡E相交于M,N兩點,記直線QM的斜率為k1,直線QN的斜率為k2,是否存在實數m使得k(k1+k2)為定值?若存在,求出m的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為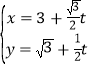 (
(![]() 為參數),點
為參數),點![]() 的極坐標為
的極坐標為![]() ,設直線
,設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“紋樣”是中國藝術寶庫的瑰寶,“火紋”是常見的一種傳統紋樣,為了測算某火紋紋樣(如圖陰影部分所示)的面積,作一個邊長為3的正方形將其包含在內,并向該正方形內隨機投擲2000個點,己知恰有800個點落在陰影部分,據此可估計陰影部分的面積是

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數![]() 的圖象上所有點的縱坐標不變,橫坐標變為原來的
的圖象上所有點的縱坐標不變,橫坐標變為原來的![]() ,再將所得圖象向右平移
,再將所得圖象向右平移![]() 個單位,若得到的圖象關于原點對稱,則當
個單位,若得到的圖象關于原點對稱,則當![]() 時,
時,![]() 的值域為( )
的值域為( )
A.![]() B.
B.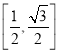 C.
C.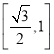 D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com