
長沙市雅禮中學(xué)2007屆高三月考試卷
數(shù) 學(xué)(文史類)
本試卷分第Ⅰ卷(選擇題)和第Ⅱ卷(非選擇題)兩部分.滿分150分,考試時(shí)間120分鐘.
參考公式: 正棱錐、圓錐的側(cè)面積公式
如果事件A、B互斥,那么

P(A+B)=P(A)+P(B)
如果事件A、B相互獨(dú)立,那么 其中,c表示底面周長、l表示斜高或
P(A?B)=P(A)?P(B) 母線長
如果事件A在1次實(shí)驗(yàn)中發(fā)生的概率是 球的體積公式
P,那么n次獨(dú)立重復(fù)實(shí)驗(yàn)中恰好發(fā)生k

次的概率 其中R表示球的半徑

第I卷(選擇題 共50分)
一.選擇題:本大題共10小題,每小題5分,共50分,在每小題給出的四個(gè)選項(xiàng)中,只有一項(xiàng)是符合要求的.
1.在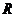 上,函數(shù)
上,函數(shù)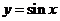 與函數(shù)
與函數(shù)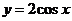 具有
具有
A.相同的單調(diào)性 B.相同的周期性 C.相同的奇偶性 D.相同的值域
2.某校現(xiàn)有高一學(xué)生210人,高二學(xué)生270人,高三學(xué)生300人,學(xué)校學(xué)生會(huì)用分層抽樣的方法從這三個(gè)年級(jí)的學(xué)生中隨機(jī)抽取n名學(xué)生進(jìn)行問卷調(diào)查,如果已知從高一學(xué)生中抽取的人數(shù)為7,那從高三學(xué)生中抽取的人數(shù)應(yīng)為
A.10 B.9 C.8 D.7
3.已知集合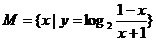 ,
,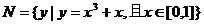 ,
,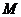 ∩
∩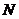 =
=
A.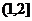 B.
B.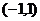 C.
C.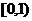 D.
D.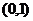
4.已知兩圓方程分別為: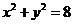 ,
,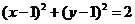 ,則兩圓的公切線方程為
,則兩圓的公切線方程為
A.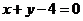 B.
B.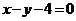 C.
C.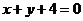 D.
D.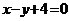
5.?dāng)?shù)列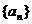 (
(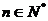 )中,
)中,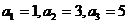 ,且
,且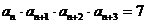 ,則
,則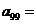
A.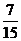 B.1 C.3
D.5
B.1 C.3
D.5
6.已知平面上不同的四點(diǎn)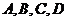 ,若
,若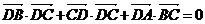 ,則
,則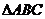 是
是
A.等腰三角形 B.等邊三角形 C.直角三角形 D.任意三角形
7.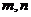 是異面直線,
是異面直線,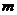 ⊥平面
⊥平面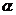 ,
,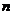 ⊥平面
⊥平面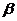 ,
,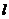 是直線,已知下列命題:
是直線,已知下列命題:
①若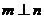 ,則
,則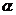 ⊥
⊥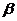 ②若
②若 ,則
,則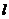 //
//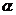 ,或
,或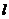 //
//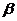
③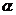 與
與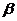 不可能平行; ④若
不可能平行; ④若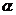 ⊥
⊥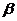 ,且
,且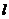 //
//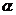 ,
,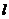 //
//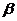 ,則
,則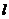 是
是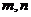 的公垂線
的公垂線
其中正確的命題是
A.①③ B.②④ C.①④ D.②③
8.在6張卡片上分別寫有1,2,3,4,5,6,將它們排成一排,得到能被4整除的6位數(shù)共有
A.144個(gè) B.120個(gè) C.192個(gè) D.168個(gè)
9.已知點(diǎn)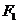 、
、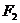 為雙曲線
為雙曲線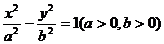 的左、右焦點(diǎn),
的左、右焦點(diǎn),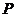 為右支上一點(diǎn),點(diǎn)
為右支上一點(diǎn),點(diǎn)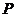 到右準(zhǔn)線的距離為
到右準(zhǔn)線的距離為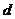 ,若
,若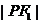 、
、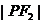 、
、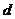 依次成等差數(shù)列,則此雙曲線離心率取值范圍是
依次成等差數(shù)列,則此雙曲線離心率取值范圍是
A.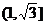 B.
B.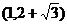 C.
C.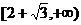 D.
D.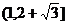
10.若函數(shù)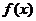 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為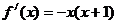 ,則函數(shù)
,則函數(shù)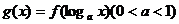 的單調(diào)遞減區(qū)間是
的單調(diào)遞減區(qū)間是
A.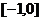 B.
B.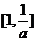 C.
C.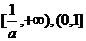 D.
D.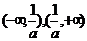
二.填空題:本大題共5小題,每小題5分,共25分,把答案填在題中橫線上.
11.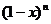 的展開式中
的展開式中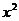 的系數(shù)是21,則
的系數(shù)是21,則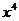 的系數(shù)為
.
的系數(shù)為
.
12.已知不等式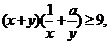 對(duì)任意正實(shí)數(shù)
對(duì)任意正實(shí)數(shù)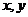 恒成立,則正實(shí)數(shù)
恒成立,則正實(shí)數(shù)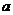 的最小值是 .
的最小值是 .
13.設(shè)函數(shù)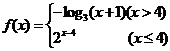 的反函數(shù)為
的反函數(shù)為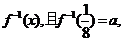
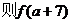 =
.
=
.
14.已知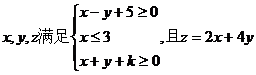 的最小值為
的最小值為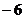 ,則常數(shù)
,則常數(shù)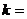 .
.
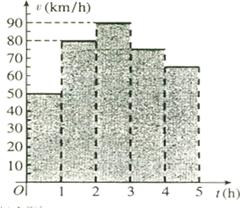 15.一輛汽車在某段路程中的行駛速度
15.一輛汽車在某段路程中的行駛速度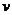 與時(shí)間
與時(shí)間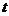
的關(guān)系如圖所示,則(i)該汽車在前3小時(shí)內(nèi)行駛的路程為 km;(ii)假設(shè)這輛汽車的里程表在汽車行駛這段路程前的讀數(shù)為
km;(ii)假設(shè)這輛汽車的里程表在汽車行駛這段路程前的讀數(shù)為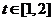 時(shí),汽車?yán)锍瘫碜x數(shù)
時(shí),汽車?yán)锍瘫碜x數(shù)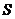 與時(shí)間
與時(shí)間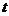 的函數(shù)解析式為
.
的函數(shù)解析式為
.
三.解答題:本大題共6小題,共75分.解答應(yīng)寫出文字說明,證明過程或演算步驟.
16.(本小題滿分12分)通訊中,發(fā)報(bào)方常采取重復(fù)發(fā)送同一信號(hào)的辦法來減少在接收中可能發(fā)生的錯(cuò)誤.假定發(fā)報(bào)機(jī)只發(fā)0和1兩種信號(hào),接收時(shí)發(fā)生錯(cuò)誤的情況是:“發(fā)0收到
17.(本小題滿分12分) 在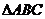 中,
中,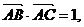
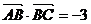 .(1)求AB邊的長度;(2)求
.(1)求AB邊的長度;(2)求 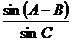 的值.
的值.
18.(本小題滿分12分) 如圖,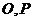 分別是正四棱柱
分別是正四棱柱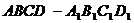 底面中心,
底面中心,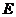 是
是
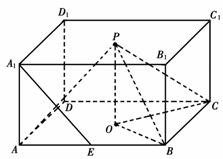
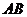 的中點(diǎn),
的中點(diǎn),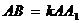 .
.
(1)求證: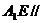 平面
平面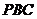 ;
;
(2)當(dāng)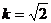 時(shí),求直線
時(shí),求直線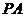 與平面
與平面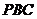
所成角的大小;
(3)當(dāng)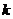 取何值時(shí),
取何值時(shí),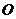 在平面
在平面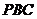 內(nèi)的射影
內(nèi)的射影
恰好為△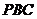 的重心?
的重心?
19.(本小題滿分12分)已知數(shù)列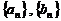 滿足
滿足 ,
,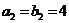 ,
,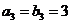 ,且
,且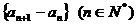 是等差數(shù)列,
是等差數(shù)列,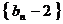
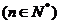 是等比數(shù)列.(1)求數(shù)列
是等比數(shù)列.(1)求數(shù)列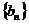 的通項(xiàng)公式;(2)求數(shù)列
的通項(xiàng)公式;(2)求數(shù)列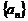 的通項(xiàng)公式;(3)是否存在
的通項(xiàng)公式;(3)是否存在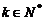 ,使
,使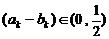 ?若存在,求出
?若存在,求出 的值,;若不存在,說明理由.
的值,;若不存在,說明理由.
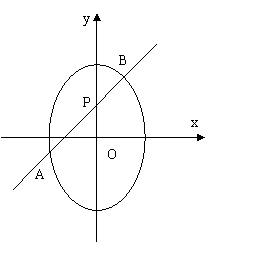 20.(本小題滿分13分)橢圓
20.(本小題滿分13分)橢圓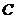 的中心為坐標(biāo)原點(diǎn),焦點(diǎn)在
的中心為坐標(biāo)原點(diǎn),焦點(diǎn)在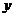 軸上,焦點(diǎn)到相應(yīng)的準(zhǔn)線的距離以及離心率均為
軸上,焦點(diǎn)到相應(yīng)的準(zhǔn)線的距離以及離心率均為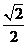 ,直線
,直線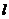 與
與
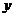 軸交于點(diǎn)
軸交于點(diǎn)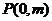 ,與橢圓
,與橢圓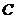 交于
交于
相異兩點(diǎn)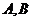 ,且
,且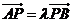 .
.
(1)求橢圓方程;
(2)若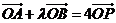 ,求
,求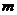 的
的
取值范圍.
21.(本小題滿分14分)已知函數(shù)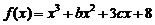 和
和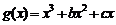 (其中
(其中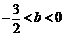 ),
),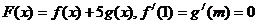 .(1)求
.(1)求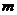 的取值范圍;
的取值范圍;
(2)方程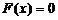 有幾個(gè)實(shí)根?為什么?
有幾個(gè)實(shí)根?為什么?
長沙市雅禮中學(xué)2007屆高三月考試卷
數(shù) 學(xué)(文史類)答案
1.B 2.A 3.C 4.A 5.D
一.選擇題:本大題共10小題,每小題5分,共50分,在每小題給出的四個(gè)選項(xiàng)中,只有一項(xiàng)是符合要求的.
6.C 7.A 8.C 9.D 10.B
二.填空題:本大題共5小題,每小題5分,共25分,把答案填在題中橫線上.
11.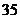
12.
13.-2
14.
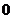
15.(i) ;(ii)
;(ii)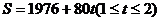
三.解答題:本大題共6小題,共75分.解答應(yīng)寫出文字說明,證明過程或演算步驟.
16.(本小題滿分12分)
解:(1)正確接收一個(gè)信號(hào)的概率為
(1-0.05)×(1-0.05)=0.9025 …………………………………………………… 2分
錯(cuò)誤接收一個(gè)信號(hào)的概率為0.05×0.05=0.0025 ……………………………… 4分
∴接收方接收一個(gè)信號(hào)的概率為0.9025+0.0025=0.905 …………………… 6分
(2)考慮對(duì)立事件,錯(cuò)誤接收一個(gè)信號(hào)的概率為
23×0.052×0.95+33×0.053=0.00725
∴正確接收一個(gè)信號(hào)的概率為1-0.00725=0.99275. …………………………12分
17.(本小題滿分12分)
解:(1)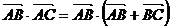
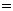
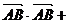
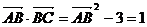 .
.
∴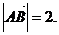 即AB邊的長度為2.………………………………………………………5分
即AB邊的長度為2.………………………………………………………5分
另解:用數(shù)量積的定義結(jié)合余弦定理即得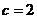 .
.
(2)由已知及(1)有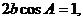
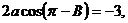
∴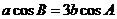 , ………………………………………………………………8分
, ………………………………………………………………8分
由正弦定理得: 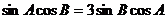 , ………………………………………10分
, ………………………………………10分
∴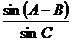 =
=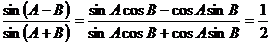 . ……………………12分
. ……………………12分
18.(本小題滿分12分)
解:(1)過P作MN∥B
∵E、M分別為AB、A1B1中點(diǎn),∴A1E∥MB
又MB⊂平面PBC,∴A1E∥平面PBC. ……………………………………………4分
(2)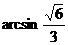 . ……………………………………………………………………8分
. ……………………………………………………………………8分
(3)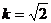 . ………………………………………………………………………12分
. ………………………………………………………………………12分
19.(本小題滿分12分)
解:(1)∵{bn-2} (nÎZ+)為等比數(shù)列,又b1-2=4,b2-2=2,b3-2=1,
\公比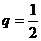 ,
,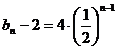 ,
,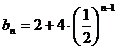 (nÎZ+) . ……………… 4分
(nÎZ+) . ……………… 4分
(2)∵{an+1-an} (nÎZ+)是等差數(shù)列,又a2-a1=-2,a3-a2=-1,\公差d=1,
an+1-an=-2+(n-1)=n-3,于是
an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=[(n-1)-3]+[(n-2)-3]+…+(1-3)+6
=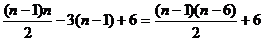 (nÎZ+). ……………………………
8分
(nÎZ+). ……………………………
8分
(3)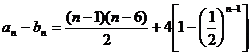 ,∵
,∵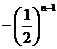 隨正整數(shù)n的增加而增加
隨正整數(shù)n的增加而增加
\當(dāng)n³6時(shí), ,
,
又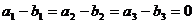 ,
, 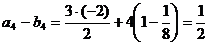 ,
,
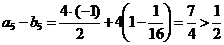 ,
,
由此可見,不存在kÎZ+,使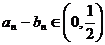 .………………………………………12分
.………………………………………12分
20.(本小題滿分13分)
解:(1)設(shè)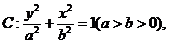 設(shè)
設(shè)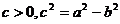 ,由條件知
,由條件知
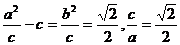 ,
,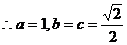 ,
,
故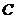 的方程為:
的方程為: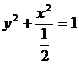 . ……………………………………………………4分
. ……………………………………………………4分
(2)由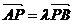 得
得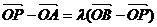
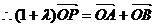 ,
,
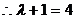 ,
, 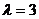 . ……………………………………………………………6分
. ……………………………………………………………6分
(另解:向量坐標(biāo)化也可以得到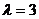 )
)
設(shè)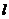 與橢圓
與橢圓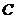 交點(diǎn)為
交點(diǎn)為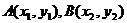
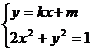 得
得
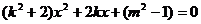 ,
,
當(dāng)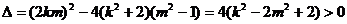 時(shí),
時(shí),
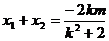 ,
,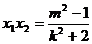 . ………………………………………………8分
. ………………………………………………8分
因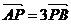 即
即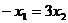 ,故
,故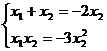 消
消 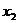 得
得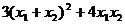 =0,
=0,
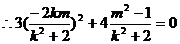 ,整理得
,整理得 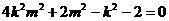 . …………10分
. …………10分
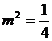 時(shí),上式不成立;所以
時(shí),上式不成立;所以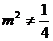 ,得
,得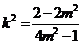 ,因
,因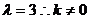
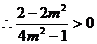 ,
,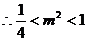 ,即
,即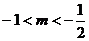 或
或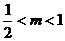 ,
,
即所求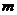 的取值范圍為
的取值范圍為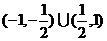 . …………………………………………13分
. …………………………………………13分
21.(本小題滿分14分)
解:(1)∵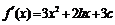 ,
,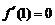 ,∴
,∴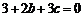 ,∴
,∴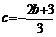 . …………1分
. …………1分
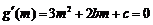 ,即
,即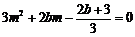 ,∴
,∴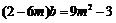 .……3分
.……3分
①當(dāng)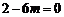 ,即
,即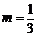 時(shí),上式不成立. …………………………………………4分
時(shí),上式不成立. …………………………………………4分
②當(dāng)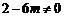 ,即
,即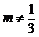 時(shí),
時(shí),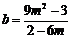 .由條件
.由條件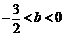 ,得到
,得到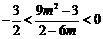 .
.
由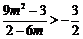 ,解得
,解得 或
或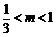 . ……………………………………………5分
. ……………………………………………5分
由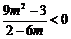 ,解得
,解得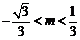 或
或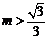 . ………………………………………6分
. ………………………………………6分
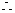 m的取值范圍是
m的取值范圍是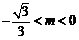 或
或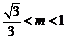 .………………………………………7分
.………………………………………7分
(2)有一個(gè)實(shí)根. ………………………………………………………………………8分
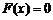 ,即
,即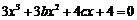 .記
.記 ,
,
則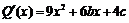 .∵
.∵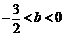 ,
,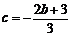
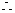
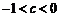 .………………10分
.………………10分
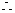 △>0,故
△>0,故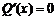 有相異兩實(shí)根
有相異兩實(shí)根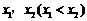 .
.
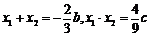 ,∴
,∴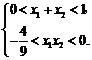 顯然
顯然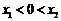 ,
,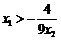 ,
,
∴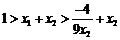 ,∴
,∴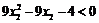 ,∴
,∴ . ………………………12分
. ………………………12分
于是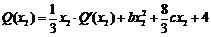
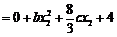
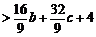
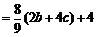
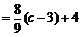
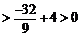 .
.
而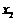 為三次函數(shù)
為三次函數(shù)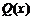 的極小值點(diǎn),故
的極小值點(diǎn),故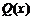 與x軸只有一個(gè)交點(diǎn).
與x軸只有一個(gè)交點(diǎn).
∴ 方程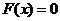 只有一個(gè)實(shí)根.……………………………………………………14分
只有一個(gè)實(shí)根.……………………………………………………14分
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com