
題目列表(包括答案和解析)
8、已知數列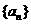 中,
中,
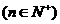 ,其前
,其前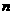 項和為
項和為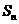 ,且
,且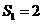 ,當
,當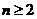 時,
時,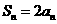 。
。
(1)求數列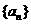 的通項公式;
的通項公式;
(2)若 ,求數列
,求數列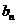 的前
的前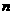 項和。
項和。
7、設函數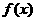 的定義域為R,當
的定義域為R,當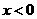 時,
時, ,且對任意的實數
,且對任意的實數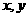
 ,有
,有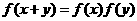
(1)求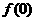 ,判斷并證明函數
,判斷并證明函數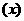 的單調性;
的單調性;
(2)數列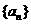 滿足
滿足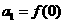 ,且
,且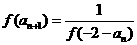
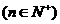
①求通項公式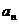 的表達式;
的表達式;
②令 ,
, …+
…+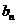 ,
, …+
…+ ,試比較
,試比較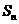 欲
欲 的大小,并加以證明。
的大小,并加以證明。
6、設數列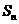 是數列
是數列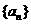 的前
的前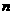 項和,滿足
項和,滿足 且
且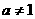 ,
, 。數列
。數列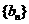 滿足
滿足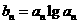
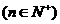
(Ⅰ)求數列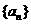 的通項公式;
的通項公式;
(Ⅱ)若數列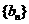 中每一項總小于它后面的項,求
中每一項總小于它后面的項,求 的取值范圍。
的取值范圍。
5、若 ,則
,則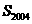 =__________
=__________
4、已知數列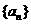 、
、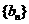 都是等差數列,
都是等差數列, ,且
,且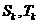 分別表示數列
分別表示數列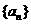 、
、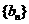 的前
的前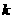 項和
項和 ,若
,若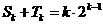 ,又有
,又有 ,求數列
,求數列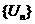 的前
的前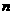 項和;欲使此和大于2004,正整數
項和;欲使此和大于2004,正整數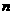 至少取何值?
至少取何值?
3、給出數陣: 其中每行、每列均為等差數列,則此數陣中所有數的和為_____
其中每行、每列均為等差數列,則此數陣中所有數的和為_____
2、已知數列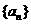 的前
的前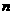 項和
項和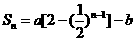
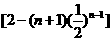
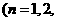 …),其中
…),其中 是非零常數,則存在數列
是非零常數,則存在數列 ,
,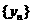 使得( )
使得( )
A、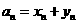 ,其中
,其中 為等差數列,
為等差數列,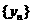 為等比數列;
為等比數列;
B、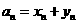 ,其中
,其中 和
和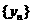 都為等差數列
都為等差數列
C、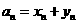 ,其中
,其中 為等差數列,
為等差數列,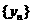 為等比數列
為等比數列
D、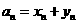 ,其中
,其中 和
和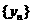 都為等比數列
都為等比數列
1、把數列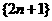 依次按第一個括號一個數,第二個括號兩個數,第三個括號三個數,第四個括號四個數,第五個括號一個數,…,循環分為:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43),…,則第104個括號內各數之和為__________
依次按第一個括號一個數,第二個括號兩個數,第三個括號三個數,第四個括號四個數,第五個括號一個數,…,循環分為:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43),…,則第104個括號內各數之和為__________
12、一個數列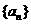 ,當
,當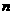 為奇數時,
為奇數時, ,求這個數列前
,求這個數列前 項的和(
項的和( 是正整數)
是正整數)
挑戰高考
11、求和: …+
…+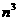
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com