
題目列表(包括答案和解析)
1.已知集合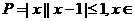 R|,
R|,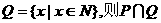 等于 ( )
等于 ( )
A.P B.Q C.{1,2} D.{0,1,2}
解:∵P=[0,2], ={0,1,2},選(D)
={0,1,2},選(D)
22.(本小題滿分14分)
已知數列{an}滿足a1=a,
an+1=1+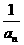 我們知道當a取不同的值時,得到不同的數列,如當a=1時,得到無窮數列:
我們知道當a取不同的值時,得到不同的數列,如當a=1時,得到無窮數列:
(Ⅰ)求當a為何值時a4=0;
(Ⅱ)設數列{bn}滿足b1=-1, bn+1=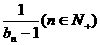 ,求證a取數列{bn}中的任一個數,都可以得到一個有窮數列{an};
,求證a取數列{bn}中的任一個數,都可以得到一個有窮數列{an};
(Ⅲ)若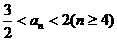 ,求a的取值范圍.
,求a的取值范圍.
解:(Ⅰ)∵a1=a,∴1+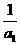 =a2,∴a2=
=a2,∴a2=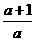 ,
, ,
,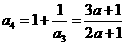 ,
,
故當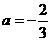 時,
時,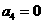
(Ⅱ)∵b1=-1,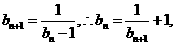
當a=b1時,a1=1+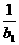 =0
=0
當a=b2時,a2=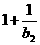 =b1,∴a2=0,
=b1,∴a2=0,
當a=b3時,a3=1+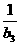 =b2,∴a3=1+
=b2,∴a3=1+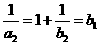 ,∴a4=0,
,∴a4=0,
……
一般地,當a=bn時,an+1=0,可得一個含育n+1項的有窮數列a1,a2,a3,…,an+1.
可用數學歸納法加以證明:
① 當n=1時,a=b1,顯然a2=0,得到一個含2項的有窮數列a1,a2.
②
假設當n=k時,a=bk,得到一個含有k+1項的有窮數列a1,a2,a3,…,ak+1,其中ak+1=0,則n=k+1時.a=bk+1,∴a2=1+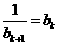 .
.
由假設可知,可得到一個含有k+1項的有窮數列a2,a3,…,ak+2,其中ak+2=0.
由①②知,對一切n∈N+,命題都成立.
(Ⅲ)要使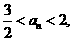 即
即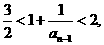 ,∴1<an-1<2.
,∴1<an-1<2.
∴要使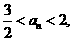 ,當且僅當它的前一項an-1,滿足1<an-1<2,∵(
,當且僅當它的前一項an-1,滿足1<an-1<2,∵(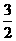 ,2)
,2)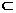 (1,2),
(1,2),
∴只須當a4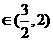 ,都有
,都有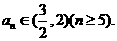
由 得
得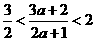 ,
,
解不等式組 得
得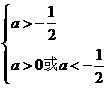 ,故a>0.
,故a>0.
21.(本小題滿分12分)
已知方向向量為v=(1,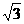 )的直線l過點(0,-2
)的直線l過點(0,-2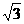 )和橢圓C:
)和橢圓C: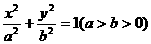 的焦點,且橢圓C的中心關于直線l的對稱點在橢圓C的右準線上.
的焦點,且橢圓C的中心關于直線l的對稱點在橢圓C的右準線上.
(Ⅰ)求橢圓C的方程;
(Ⅱ)是否存在過點E(-2,0)的直線m交橢圓C于點M、N,滿足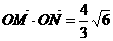 ,
,
cot∠MON≠0(O為原點).若存在,求直線m的方程;若不存在,請說明理由.

解:(Ⅰ)由題意可得直線ι: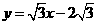 ,
①
,
①
過原點垂直ι的方程為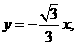 ②
②
解①②得x=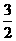 .∵橢圓中心O(0,0)關于直線ι的對稱點在橢圓C的右準線上,
.∵橢圓中心O(0,0)關于直線ι的對稱點在橢圓C的右準線上,
∴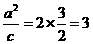 .∵直線ι過橢圓焦點,∴該焦點坐標為(2,0).
.∵直線ι過橢圓焦點,∴該焦點坐標為(2,0).
∴a2=6,c=2,b2=2,故橢圓C的方程為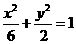 . ③
. ③
(Ⅱ)設M(x1,y1),N(x2,y2),當直線m不垂直x軸時,直線m:y=k(x+2)代入③,整理得
(3k2+1)x2+12k2x+12k2-6=0,則x1+x2=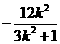 ,x1x2=
,x1x2=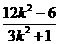 ,
,
|MN|=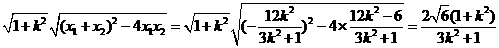
點O到直線MN的距離d=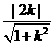 .∵
.∵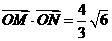 cot∠MON,即
cot∠MON,即
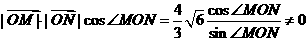 ,
,
∴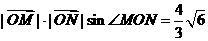 ,∴
,∴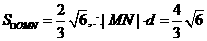 ,
,
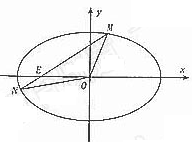
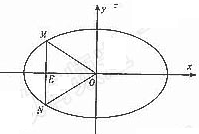 即
即 .整理得
.整理得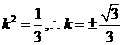 .
.
當直線m垂直x軸時,也滿足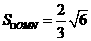
故直線m的方程為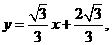 或y=
或y=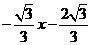 或x=-2.
或x=-2.
經檢驗上述直線均滿足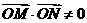 .
.
所在所求直線方程為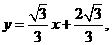 或y=
或y=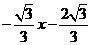 或x=-2..
或x=-2..
20.(本小題滿分12分)
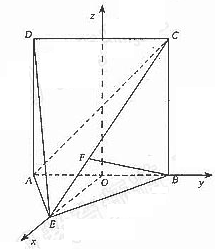
如圖,直二面角D-AB-E中,四邊形ABCD是邊長為2的正方形,AE=EB,F為CE上的點,且BF⊥平面ACE.
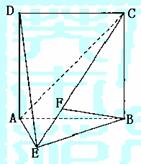 (Ⅰ)求證AE⊥平面BCE;
(Ⅰ)求證AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的大小;
(Ⅲ)求點D到平面ACE的距離.
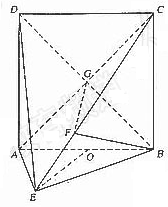
解法一:(Ⅰ) ∵BF⊥平面ACE,∴BF⊥AE,∵二面角D-AB-E為直二面角,且CB⊥AB,
∴CB⊥平面ABE,∴CB⊥AE,∴AE⊥平面BCE
(Ⅱ)連結BD交AC于G,連結FG,∵正方形ABCD邊長為2,∴BG⊥AC,BG=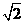 ,
,
∵BF⊥平面ACE,由三垂線定理的逆定理得FG⊥AC,∴∠BCF是二面角B-AC-E的平面角,
由(Ⅰ)AE⊥平面BCE,∴AE⊥EB.又∵AE=EB,∴在等腰直角三角形中,BE=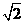 .
.
又∵直角三角形BCE中,EC=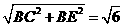 ,BF=
,BF=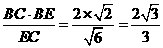
∴直角三角形BFG中,sin∠BGF=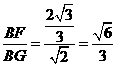 ,∴二面角B-AC-E等于arcsin
,∴二面角B-AC-E等于arcsin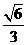 .
.
,(Ⅲ)過E作EO⊥AB交AB于O,OE=1,∵二面角D-AB-E為直二面角,∴EO⊥平面ABCD.
設D到平面ACE的距離為h,∵ ,∴
,∴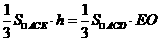 .
.
∵AE⊥平面BCE,∴AE⊥EC.∴h=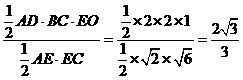 .
.
∴點D點D到平面ACE的距離為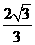 .
.
解法二:(Ⅰ)同解法一.
(Ⅱ)以線段AB的中點為原點O,OE所在直線為x軸,AB所在直線為y軸,過O點平行于AD的直線為z軸,建立空間直角坐標系O-xyz,如圖
∵AE⊥平面BCE,BE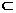 面BCE,∴AE⊥BE,在直角三角形AEB中,AB=2,O為AB的中點
面BCE,∴AE⊥BE,在直角三角形AEB中,AB=2,O為AB的中點
∴OE=1,A(0,-1,0),E(1,0,0),C(0,1,2),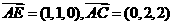
 設平面AEC的一個法向量
設平面AEC的一個法向量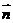 =(x,y,z),則
=(x,y,z),則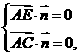 即
即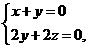 解得
解得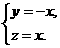
令x=1,得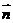 =(1,-1,1)是平面EAC的一個法向量,又平面BAC的一個法向量為
=(1,-1,1)是平面EAC的一個法向量,又平面BAC的一個法向量為 =(1,0,0),
=(1,0,0),
∴cos(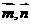 )=
)=
∴二面角B-AC-E的大小為arccos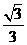 .
.
(Ⅲ)∵AD∥z軸,AD=2,∴ ,∴點D到平面ACE的距離
,∴點D到平面ACE的距離
d=|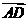 |
|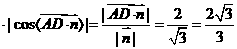 .
.
19.(本小題滿分12分)
已知函數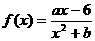 的圖象在點M(-1,f(x))處的切線方程為x+2y+5=0.
的圖象在點M(-1,f(x))處的切線方程為x+2y+5=0.
(Ⅰ)求函數y=f(x)的解析式;
(Ⅱ)求函數y=f(x)的單調區間.
解:(Ⅰ)由函數f(x)的圖象在點(-1,f(-1))處的切線方程為x+2y+5=0,知-1+2f(-1)+5=0,即f(-1)=-2,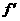 (-1)=
(-1)=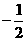 .∵
.∵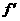 (x)=
(x)=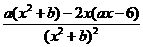 ,∴
,∴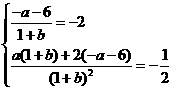
即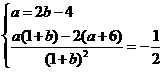 解得a=2,b=3(∵b+1≠0,∴b=-1舍去)
解得a=2,b=3(∵b+1≠0,∴b=-1舍去)
∴所求函數y=f(x)的解析式是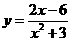
(Ⅱ)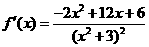 ,令-2x2+12x+6=0,解得x1=
,令-2x2+12x+6=0,解得x1=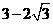 ,x2=
,x2=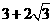
當x<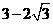 ,或x>
,或x>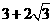 時,
時, ;當
;當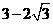 <x<時,
<x<時,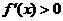 ,
,
所以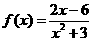 在(-∞,
在(-∞, 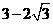 )內是減函數;在(
)內是減函數;在(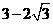 ,
,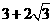 )內是增函數;
)內是增函數;
在(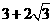 ,+∞)內是減函數
,+∞)內是減函數
18.(本小題滿分12分)
甲、乙兩人在罰球線投球命中的概率分別為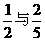 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.
(Ⅰ)甲、乙兩人在罰球線各投球一次,求兩人得分之和ξ的數學期望;
(Ⅱ)甲、乙兩人在罰球線各投球二次,求這四次投球中至少一次命中的概率;
解:(Ⅰ)依題意,記“甲投一次命中”為事件A,“乙投一次命中”為事件B,則
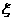 |
0 |
1 |
2 |
|
P |
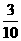 |
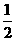 |
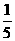 |
P(A)=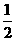 ,P(B)=
,P(B)=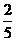 ,P(
,P( )=
)=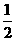 ,P(
,P(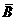 )=
)=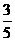 ,甲、乙兩人得分之和
,甲、乙兩人得分之和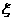 的可取值為0、1、2,則
的可取值為0、1、2,則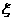 概率分布為
概率分布為
E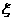 =0×
=0×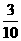 +1×
+1×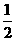 +2×
+2×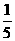 =
=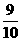
答:甲、乙兩人在罰球線各投球一次,兩人得分之和ξ的數學期望為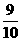
(Ⅱ)∵事件“甲、乙兩人在罰球線各投球二次不命中” 的概率是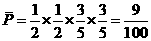
∴甲、乙兩人在罰球線各投球二次,至少有一次命中的概率為P=1-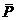 =1-
=1-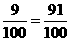
答:甲、乙兩人在罰球線各投球二次,至少有一次命中的概率為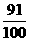 .
.
17.(本小題滿分12分)
已知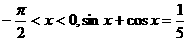 .
.
(I)求sinx-cosx的值;
(Ⅱ)求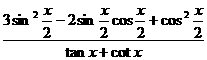 的值.
的值.
解:(Ⅰ)由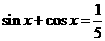 ,得
,得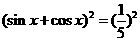 ,得2sinxcosx=
,得2sinxcosx=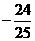 ,∵(sinx-cosxx)2=1-2sinxcosx=
,∵(sinx-cosxx)2=1-2sinxcosx=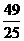 ,又
,又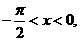 ∴sinx<0cosx>0,∴sinx-cosx=-
∴sinx<0cosx>0,∴sinx-cosx=-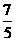
(Ⅱ) 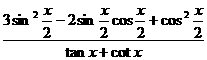 =
=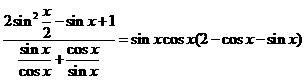
=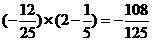
16.把下面不完整的命題補充完整,并使之成為真命題:
若函數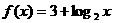 的圖象與
的圖象與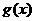 的圖象關于
對稱,則函數
的圖象關于
對稱,則函數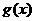 =
=
。
解:若函數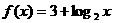 的圖象與
的圖象與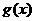 的圖象關于y=x對稱, 則函數
的圖象關于y=x對稱, 則函數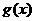 =2x-3.
=2x-3.
(注:填上你認為可以成為真命題的一件情形即可,不必考慮所有可能的情形).
15.若常數b滿足|b|>1,則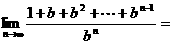 .
.
解: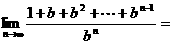
 =
=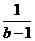
14.非負實數 滿足
滿足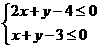 則x+3y的最大值為
。
則x+3y的最大值為
。
解: 如右圖,在同一平面直角坐標系中畫出下列
如右圖,在同一平面直角坐標系中畫出下列
曲線方程的圖象:
2x+y-4=0 (x≥0,y≥0)
x+y-3=0 (x≥0,y≥0)
它們分別是線段AB,CD
則非負實數x、y滿足的不等式組
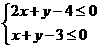 表示的區域為DMAO,令x+3y=b,
表示的區域為DMAO,令x+3y=b,
使直線系x+3y=b通過區域DMAO且使b為取得最大值,當且僅當直線x+3y=b過點D(0,3)這時最大值b=9.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com