
2005/2006學年度江蘇鹽城市高三第二次調研考試
數 學 試 題
第Ⅰ卷(選擇題 共60分)
 一.選擇題: 本大題共12小題,每小題5分,共60分.在每小題給出的四個選項中,只有一個是符合題目要求的.
一.選擇題: 本大題共12小題,每小題5分,共60分.在每小題給出的四個選項中,只有一個是符合題目要求的.
1.設全集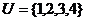 兩個集合
兩個集合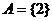 ,
,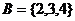 ,則
等于
,則
等于
A. {1} B. {1,3,4} C. {2} D. {3,4}
2. 在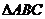 中,
中,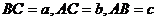 ,如果
,如果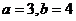 ,那么“
,那么“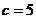 ”是“
”是“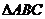 為直角三角形”的
為直角三角形”的
A.充分不必要條件 B.必要不充分條件
C. 充要條件 D.既不是充分又不是必要條件
3. 若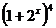 的展開式的第3項為12,則x等于
的展開式的第3項為12,則x等于
A.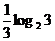 B.
B.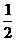 C.
C.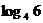 D.2
D.2
4.拋物線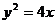 上點
上點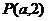 到焦點F的距離為
到焦點F的距離為
A. 1 B.
5.已知數列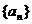 的通項公式為
的通項公式為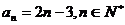 ,其前n項和為
,其前n項和為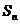 ,則使
,則使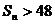 成立的n的最小值為
成立的n的最小值為
A .7 B.
6. 函數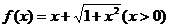 的反函數是
的反函數是
A.  B.
B.
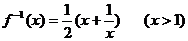
C. 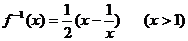 D.
D.
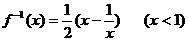
7. 已知函數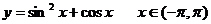 ,則下列正確的是
,則下列正確的是
A. 是偶函數,有最大值為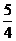 B. 是偶函數,有最小值為
B. 是偶函數,有最小值為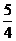
C. 是偶函數,有最大值為2 D. 是奇函數,沒有最小值
8. 設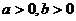 ,則以下不等式中不恒成立的是
,則以下不等式中不恒成立的是
A. 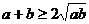 B.
B. 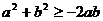
C. 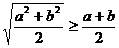 D.
D. 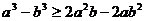
9. 如果x、y滿足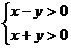 ,則有
,則有
A. 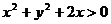 B.
B.
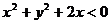
C. 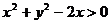 D.
D.
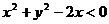
10. 已知向量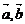 是兩個不共線的非零向量, 向量
是兩個不共線的非零向量, 向量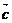 滿足
滿足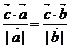 .則向量
.則向量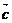 用向量
用向量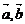 一定可以表示為
一定可以表示為
A. 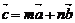 且
且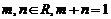 . B.
. B. 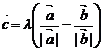
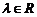
C. 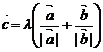
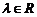
D. 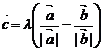
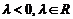 , 或
, 或 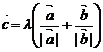
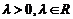
二、填空題:本大題共4小題,t每小題4分共16分.
13.函數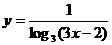 的定義域是
.
的定義域是
.
14.已知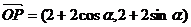 ,
,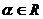 ,(O為坐標原點),向量
,(O為坐標原點),向量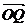 滿足
滿足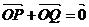 ,則動點Q的軌跡方程是
.
,則動點Q的軌跡方程是
.
15.對共有10人的一個數學小組做一次數學測驗,測試題由10道單項選擇題構成,每答對1題得5分,答錯或不答得0分,批閱后的統計得分情況如下
得分
50分
 45分
45分
 40分
40分
 35分
35分
人數
2
4
8
10
則這次測試的平均成績為 .
 16.在正四棱柱
16.在正四棱柱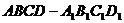 中,如果底邊正方形ABCD的邊長
中,如果底邊正方形ABCD的邊長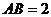 ,側棱
,側棱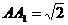 ,則下列四個命題:
,則下列四個命題:
①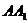 與
與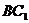 成
成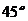 角;
角;
② 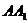 與
與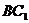 的距離為2 ;
的距離為2 ;
③ 二面角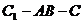 為
為 ;
;
④ 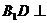 平面
平面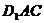 .
.
則正確命題的序號為 .
17、已知兩個函數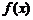 和
和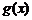 的定義域和值域都是集合{1,2,3},其定義如下表.
的定義域和值域都是集合{1,2,3},其定義如下表.
x
1
2
3
f(x)
2
3
1
x
1
2
3
g(x)
1
3
2
填寫下列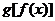 的表格
的表格
x
1
2
3
g (f(x))
18、現要給四棱錐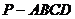 的五個面涂上顏色,要求相鄰的面涂不同的顏色,可供選擇的顏色共有4種,則不同的涂色方案的種數共有
種。
的五個面涂上顏色,要求相鄰的面涂不同的顏色,可供選擇的顏色共有4種,則不同的涂色方案的種數共有
種。
三、解答題:本大題共5小題,共70分.解答應寫出文字說明,x證明過程或演算步驟.
17.( 本小題滿分12分)
黃種人群中各種血型的人所占的比如下表所示:
血型
A
B
AB
O
該血型的人所占/%
28
29
8
35
已知同種血型的人可以輸血,O型血可以輸給任一種血型的個人,任何人的血都可以輸給AB型的人,其他不同血型的人不能互相輸血.小明是B型血,若小明需要輸血,問:
(1)任找一個人,其血可以輸給小明的概率是多少?
(2)任找兩個人,當中至少有一個人,其血可以輸給小明的概率是多少?
18. ( 本小題滿分14分)
 如圖,三棱錐
如圖,三棱錐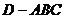 中,
中,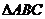 是邊長為4的正三角形,
是邊長為4的正三角形,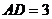 ,E為AB的中點,
,E為AB的中點, .
.
(1) 求證:平面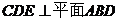 ;
;
(2) 求直線 和平面CDE所成的角的大小;
和平面CDE所成的角的大小;
(3) 求點A到平面BCD的距離.
19. ( 本小題滿分14分)
已知正數數列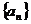 中,
中,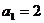 .若關于
.若關于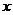 的方程
的方程
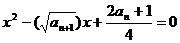
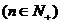 有相等的實根.
有相等的實根.
(1)求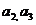 的值;
的值;
(2)求證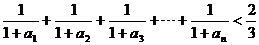
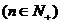 .
.
20. ( 本小題滿分15分)
已知雙曲線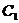 的方程為
的方程為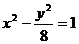 ,橢圓
,橢圓 長軸的兩個端點恰好為雙曲線
長軸的兩個端點恰好為雙曲線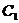 的兩個焦點.
的兩個焦點.
(1)如果橢圓 的兩個焦點又是雙曲線的兩個頂點,求橢圓
的兩個焦點又是雙曲線的兩個頂點,求橢圓 的方程;
的方程;
(2)如果橢圓 的方程為
的方程為 ,且橢圓
,且橢圓 上存在兩點A,B關于直線
上存在兩點A,B關于直線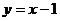 對稱,求
對稱,求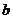 取值范圍.
取值范圍.
21.( 本小題滿分15分)
已知函數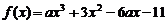 ,
,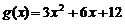 ,和直線m:
,和直線m: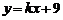 .又
.又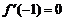 .
.
(1)求a的值;
(2)是否存在k的值,使直線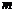 既是曲線y=f(x)的切線,又是y=g(x)
的切線;如果存在,求出k的值;如果不存在,說明理由.
既是曲線y=f(x)的切線,又是y=g(x)
的切線;如果存在,求出k的值;如果不存在,說明理由.
(3)如果對于所有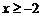 的x,都有
的x,都有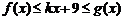 成立,求k的取值范圍.
成立,求k的取值范圍.
鹽城市2005/2006學年度高三第二次調研考試
tx數 學 試 卷 答 案
1.D 2.A 3.B 4.B 5.C 6.C 7.A 8.D 9. A 10.C
11. 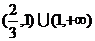 12.
12. 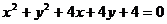 13. 42 14. ②③ 15.3,2,1 16.72
13. 42 14. ②③ 15.3,2,1 16.72
18. (1)對于任一個人,其血型為A,B,AB,O型的事件分別記為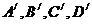 ,它們是互斥的,由已知,有
,它們是互斥的,由已知,有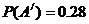 ,
,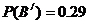
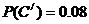
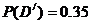
因為B,O型血可以輸給B型血的人,故“可以輸給B型血的人”為事件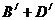
根據互斥事件的加法公式,有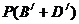 =
=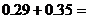
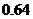 .
.
所以任何一人.其血可以輸給小明的概率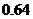
(2) 由于A,AB型血不能輸給B型血的人,一個人“不能輸給B型的人”為事件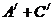
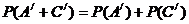 =
=
“任何兩個人,其中至少有一個人,可以輸給小明”的事件記為E,他的對立事件為:兩個人都不能輸血給小明,則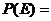
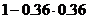 =
=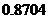 .
.
所以,任何二個人,其中至少有一個人,其血可以輸給小明的概率為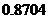
答:略
19. (1) 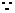
 ,
,

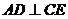 ,又
,又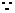
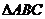 為正三角形,E為AB的中點,
為正三角形,E為AB的中點,
 而
而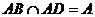

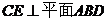 ,又
,又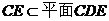

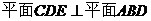
(2)由(1)得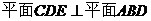 ,
, AD在平面CDE上的射影為DE
AD在平面CDE上的射影為DE
所以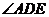 即為所成的角.
即為所成的角.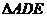 為
為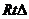 ,且AE=2,AD=3,
,且AE=2,AD=3,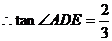

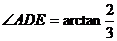 ,即直線AD與平面CDE所成的角為
,即直線AD與平面CDE所成的角為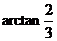
(3)取BC的中點M,連接DM,過A點在平面DAM內作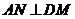 于N
于N
證得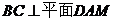 ,所以
,所以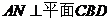
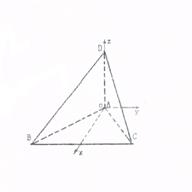 AM=
AM=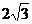 ,DM=
,DM=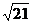 ,
,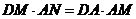 所以
所以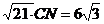
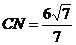
(方法2)(10建立看見直角坐標系(如圖)
∵E為AB的中點,∴E點坐標為(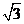 。-3,0),
。-3,0),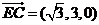
設平面CDE的法向量m=(s,t,1)
則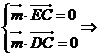
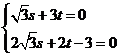 ∴
∴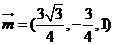
又平面ABD的法向量為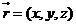 ∵
∵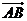 =(
=(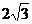 。-2,0)
。-2,0) 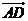 =(0,0,3)
=(0,0,3)
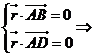
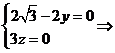
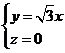 不妨設x=1,則
不妨設x=1,則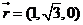
而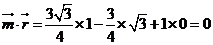 ∴
∴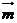 ⊥
⊥ ∴平面CDE⊥平面ABD
∴平面CDE⊥平面ABD
(2)設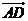 與
與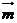 的夾角為
的夾角為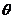 ,則cos
,則cos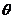 =
=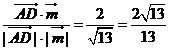
∴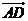 與
與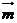 的夾角為arccos
的夾角為arccos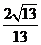 即AD與平面CDE所成的角為
即AD與平面CDE所成的角為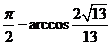
(3)則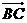 =(0,4,0),
=(0,4,0), =(2
=(2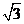 ,2,-3),
,2,-3),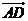 =(0,0,3)設平面BCD的法向量為
=(0,0,3)設平面BCD的法向量為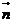 =(p,q,1)
=(p,q,1)
則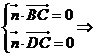

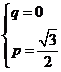 則
則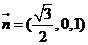
向量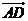 =(0,0,3)在
=(0,0,3)在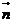 =(
=( ,0,1)上的投影為
,0,1)上的投影為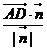 =
=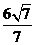
20.解:(1)由題意得 得
得 得
得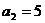 ,
,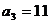
(2)由于 =
=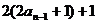 =
=
=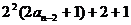 =
=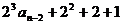 =
=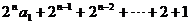 =
=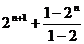 =
=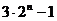

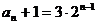
或:∵an+1=2an+1 ∴an+1+1=2(an+1) ∴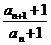 =2 ∵a1+1=2+1=3 ∴an+1=3?2n-1
=2 ∵a1+1=2+1=3 ∴an+1=3?2n-1
則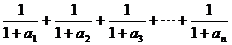 =
=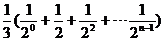
=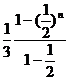 =
=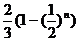
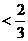 所以
所以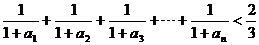
21.解(1)在雙曲線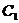 的方程
的方程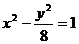 中
中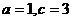 ,則橢圓
,則橢圓 方程為
方程為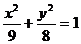
(2)橢圓 方程為
方程為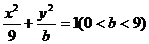 , A、B點所在直線方程設為
, A、B點所在直線方程設為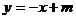 ,
,
代入橢圓 方程得
方程得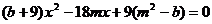
由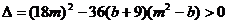 得
得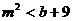 設
設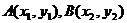 那么
那么
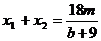 ,
, 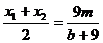 ,所以
,所以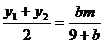
將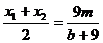 ,
,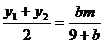
代入直線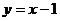 得
得 再將
再將 代入
代入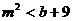 得
得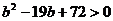 ,
,
解得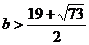 (舍去)或
(舍去)或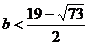 ,
,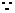
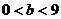

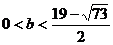
22.解:(1)因為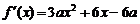 ,所以
,所以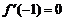 即
即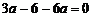 ,所以a=-2.
,所以a=-2.
(2)因為直線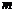 恒過點(0,9).
恒過點(0,9).
先求直線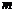 是y=g(x)
的切線.設切點為
是y=g(x)
的切線.設切點為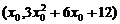 ,因為
,因為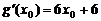 .
.
所以切線方程為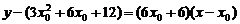 ,將點(0,9)代入得
,將點(0,9)代入得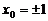 .
.
當 時,切線方程為y=9,
當
時,切線方程為y=9,
當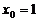 時,切線方程為y=12x+9.
時,切線方程為y=12x+9.
由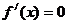 得
得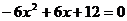 ,即有
,即有
當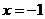 時,
時,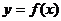 的切線
的切線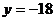 ,
,
當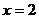 時,
時, 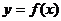 的切線方程為
的切線方程為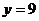

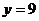 是公切線,
是公切線,
又由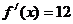 得
得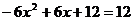

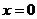 或
或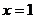 ,
,
當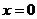 時
時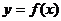 的切線為
的切線為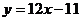 ,
,
當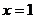 時
時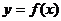 的切線為
的切線為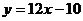 ,
,
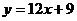 ,不是公切線
,不是公切線
綜上所述 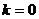 時
時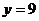 是兩曲線的公切線
是兩曲線的公切線
(3).(1)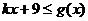 得
得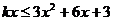 ,當
,當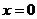 ,不等式恒成立,
,不等式恒成立,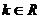 .
.
當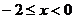 時,不等式為
時,不等式為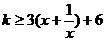 ,
,
而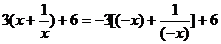
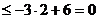
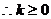
當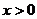 時,不等式為
時,不等式為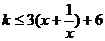 ,
,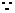
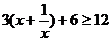

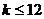
 當
當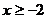 時,
時,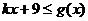 恒成立,則
恒成立,則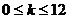
(2)由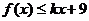 得
得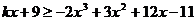
當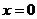 時,
時,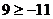 恒成立,
恒成立,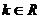 ,當
,當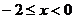 時有
時有
設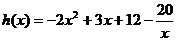 =
=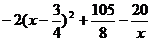 ,
,
當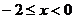 時
時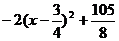 為增函數,
為增函數,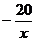 也為增函數
也為增函數

 要使
要使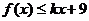 在
在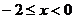 上恒成立,則
上恒成立,則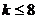
由上述過程只要考慮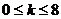 ,則當
,則當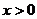 時
時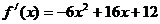 =
=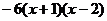
 在
在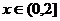 時
時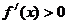 ,在
,在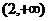 時
時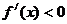

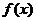 在
在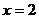 時有極大值即
時有極大值即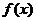 在
在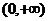 上的最大值,又
上的最大值,又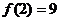 ,即
,即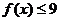 而當
而當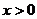 ,
,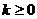 時
時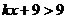 ,
,
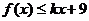 一定成立
一定成立
綜上所述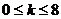 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com