
福建省東山二中2007屆高三第一次適應性測試
數學理科試題
一、選擇題(共60分)
1、復數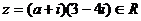 ,則實數a的值是( )
,則實數a的值是( )
A.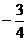 B.
B.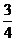 C.
C.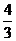 D.-
D.-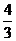
2、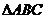 中,若
中,若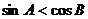 ,則
,則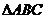 為
( )
為
( )
A、銳角三角形 B、直角三角形 C、鈍角三角形 D、不能確定
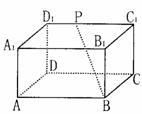 3、如右圖,長方體ABCD―A1B
3、如右圖,長方體ABCD―A1B
A.是45° B.是60°
C.是90° D.隨P點的移動而變化
4、設函數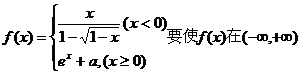 內連續,則實數a值等于( )
內連續,則實數a值等于( )
A.1 B.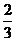 C.
C.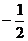 D.
D.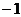
5、關于函數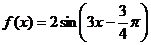 ,有下列命題
,有下列命題
① 其最小正周期為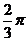 ; ② 其圖像由
; ② 其圖像由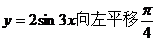 個單位而得到;
個單位而得到;
③ 其表達式寫成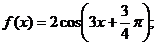 ④ 在
④ 在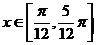 為單調遞增函數;
為單調遞增函數;
則其中假命題為( )
A.① B.② C.③ D.④
6、已知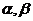 表示平面,m,n表示直線,則m//
表示平面,m,n表示直線,則m//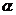 的一個充分而不必要條件是( )
的一個充分而不必要條件是( )
A.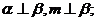 B.
B.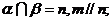 C.
C.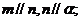 D.
D.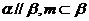
7、若函數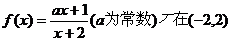 內為增函數,則實數a的取值范圍( )
內為增函數,則實數a的取值范圍( )
A.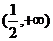 B.
B.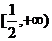 C.
C.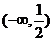 D.
D.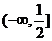
8、已知雙曲線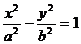 的左焦點為F1,左、右頂點為A1、A2,P為雙曲線上任意一點,則分別以線段PF1,A
的左焦點為F1,左、右頂點為A1、A2,P為雙曲線上任意一點,則分別以線段PF1,A
A.相交 B.相切 C.相離 D.以上情況都有可能
 9、如圖,平面內的兩條相交直線
9、如圖,平面內的兩條相交直線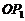 和
和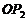 將該平面分割成四個部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括邊界). 若
將該平面分割成四個部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括邊界). 若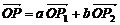 ,且點
,且點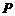 落在第Ⅲ部分,則實數
落在第Ⅲ部分,則實數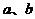 滿足( )
滿足( )
(A) 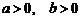 .
(B)
.
(B) 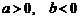 .
.
(C) 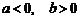 .
(D)
.
(D) 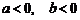 .
.
10、在一次教師聯歡會上,到會的女教師比男教師多12人,從這些教師中隨機挑選一人表演節目. 若選到男教師的概率為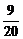 ,則參加聯歡會的教師共有( )
,則參加聯歡會的教師共有( )
A.120人. B.144人 C.240人 D.360人
11、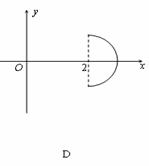
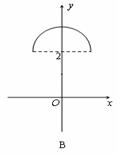
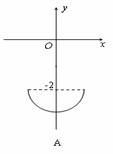
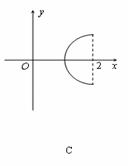 在平面直角坐標系中,已知曲線C:
在平面直角坐標系中,已知曲線C: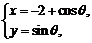 (θ是參數,且
(θ是參數,且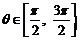 ),那么曲線C關于直線y=x對稱的曲線是 ( )
),那么曲線C關于直線y=x對稱的曲線是 ( )
12、若不等式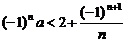 對于任意正整數n恒成立,則實數a的取值范圍是( )
對于任意正整數n恒成立,則實數a的取值范圍是( )
A.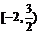 B.
B.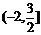 C.
C.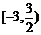 D.
D.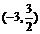
二、填空題(共16分)
13、已知數列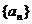 滿足
滿足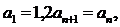 記
記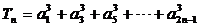 ,
,
則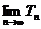 = .
= .
14、已知函數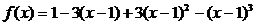 ,則
,則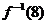 =
.
=
.
15、已知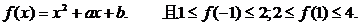 則點
則點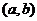 所在區域面積是
所在區域面積是
16、點P(3,1)在橢圓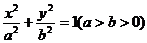
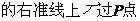
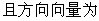 的
的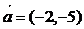 光線經直線y=-2反射后通過橢圓的右焦點,則這個橢橢圓的離心率為
光線經直線y=-2反射后通過橢圓的右焦點,則這個橢橢圓的離心率為
三、解答題(共74分)
17、(本小題12分) 已知函數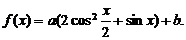
(1)當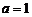 時,求
時,求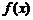 的單調遞增區間;
的單調遞增區間;
(2)當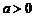 ,且
,且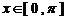 時,
時,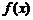 的值域是
的值域是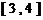 ,求a、b的值.
,求a、b的值.
18、(本小題12分)
旅游公司為3個旅游團提供4條旅游線路,每個旅游團任選其中一條.
(1)求3個旅游團選擇3條不同的線路的概率
(2)求恰有2條線路沒有被選擇的概率.
(3)求選擇甲線路旅游團數的期望.
19、(本小題12分) 如圖,直四棱柱ABCD―A1B
(1)求二面角O1-BC-D的大小;
(2)求點E到平面O1BC的距離
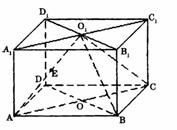
20、(本小題12分)
在平面直角坐標系中,已知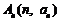 、
、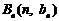 、
、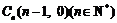 ,滿足向量
,滿足向量
 與向量
與向量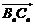 共線,且點
共線,且點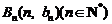 都在斜率為6的同一條直線上.
都在斜率為6的同一條直線上.
(1)試用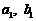 與n來表示
與n來表示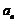 ;
;
(2)設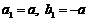 ,且12<a≤15,求數列
,且12<a≤15,求數列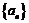 中的最小值的項.
中的最小值的項.
21、(本小題12分)已知雙曲線C的中心在原點,拋物線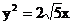 的焦點是雙曲線C的一個焦點,且雙曲線過點(1,
的焦點是雙曲線C的一個焦點,且雙曲線過點(1, 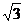 ).
).
(1)求雙曲線的方程;
(2)設直線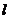 :
: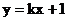 與雙曲線C交于A、B兩點, 試問:
與雙曲線C交于A、B兩點, 試問:
① 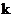 為何值時
為何值時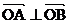
② 是否存在實數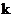 , 使A、B兩點關于直線
, 使A、B兩點關于直線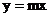 對稱(
對稱(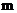 為常數), 若存在,
求出
為常數), 若存在,
求出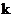 的值; 若不存在,
請說明理由.
的值; 若不存在,
請說明理由.
22、.(本小題14分) 設函數f(x)=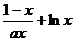 在[1+,∞
在[1+,∞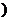 上為增函數.
上為增函數.
(1)求正實數a的取值范圍.
(2)若a=1,求征: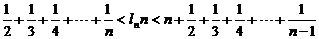
(n∈N*且n≥2)
一、選擇題(60分)
BCCA BDAB BAAA
二、填空題(16分)
13、
14、0
15、1
16、
三、解答題(74分)
17、解(1) ,
,
∴遞增區間為 ----------------------6分
----------------------6分
(2)
而 ,
,
故 --------------- 12分
--------------- 12分
18、解:(1)3個旅游團選擇3條不同線路的概率為:P1= …………3分
…………3分
(2)恰有兩條線路沒有被選擇的概率為:P2= ……6分
……6分
(3)設選擇甲線路旅游團數為ξ,則ξ=0,1,2,3
P(ξ=0)= P(ξ=1)=
P(ξ=1)=
P(ξ=2)=  P(ξ=3)=
P(ξ=3)= 
ξ
0
1
2
3




∴ξ的分布列為:
∴期望Eξ=0× +1×
+1× +2×
+2× +3×
+3× =
= ………………12分
………………12分
19、