
江蘇省南通市2009屆高三數學押題卷(一)
一、填空題:本大題共14小題,每小題5分,共70分. 不需寫出解答過程.請把答案直接填寫在答案卷上.
1.函數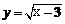 的定義域為______ .
的定義域為______ .
2.設 ,且
,且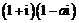 為純虛數,則
為純虛數,則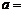 ______.
______.
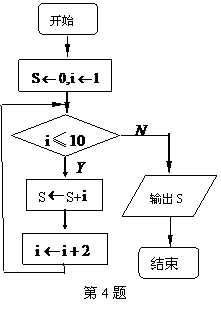 3.如圖(
3.如圖(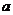 ),直三棱柱的側棱長和底面邊長均為2,正視圖和俯視圖如圖(b),(c)所示,則其左視圖的面積為_______________.
),直三棱柱的側棱長和底面邊長均為2,正視圖和俯視圖如圖(b),(c)所示,則其左視圖的面積為_______________.
4.如果執行如圖的流程圖,那么輸出的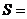 .
.
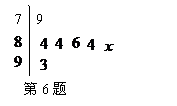 5.已知雙曲線
5.已知雙曲線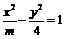 的一條漸近線的方程為
的一條漸近線的方程為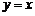 ,則此雙曲線兩條準線間距離為_____.
,則此雙曲線兩條準線間距離為_____.
6.如圖是某次青年歌手電視大獎賽上一位選手得分的莖葉統計圖,
但是有一個數字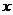 不清晰.根據比賽規則要去掉一個最高分和一個
不清晰.根據比賽規則要去掉一個最高分和一個
最低分.已知所剩數據的平均數為85,則所剩數據的方差為 _____ .
.
7.利用計算機在區間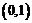 上產生兩個隨機數
上產生兩個隨機數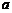 和
和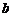 ,則方程
,則方程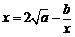 有實根的概率為 .
有實根的概率為 .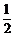
8.已知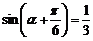 ,則
,則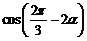 的值等于________.
的值等于________.
9.某單位用3.2萬元購買了一臺實驗儀器,假設這臺儀器從啟用的第一天起連續使用,第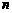 天的維修保養費為
天的維修保養費為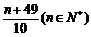 元,若使用這臺儀器的日平均費用最少,則一共使用了 天.
元,若使用這臺儀器的日平均費用最少,則一共使用了 天.
10.連續2次拋擲一枚骰子(六個面上分別標有數字1,2,3,4,5,6),記“兩次向上的數字之和等于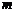 ”為事件
”為事件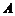 ,則
,則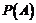 最大時,
最大時,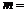 .
.
11. 已知下列兩個命題:
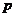 :
: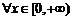 ,不等式
,不等式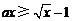 恒成立;
恒成立;
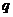 :1是關于x的不等式
:1是關于x的不等式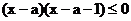 的一個解.
的一個解.
若兩個命題中有且只有一個是真命題,則實數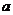 的取值范圍是
.
的取值范圍是
.
12.定義一個對應法則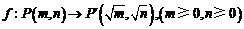 .現有點
.現有點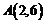 與
與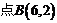 ,點
,點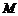 是
是
線段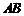 上一動點,按定義的對應法則
上一動點,按定義的對應法則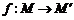 .當點
.當點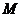 在線段
在線段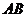 上從點
上從點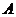 開始運動到點
開始運動到點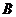 結束時,點
結束時,點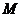 的對應點
的對應點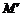 所經過的路線長度為 .
所經過的路線長度為 .
13.設曲線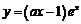 在點
在點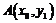 處的切線為
處的切線為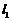 ,曲線
,曲線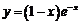 在點
在點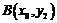 處的切線為
處的切線為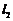 ,若存在
,若存在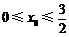 ,使得
,使得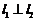 ,則實數
,則實數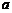 的取值范圍是
.
的取值范圍是
.
14.數列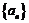 滿足
滿足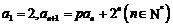 ,其中
,其中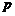 為常數.若存在實數
為常數.若存在實數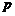 ,使得數列
,使得數列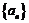 為等差數列或等比數列,則數列
為等差數列或等比數列,則數列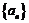 的通項公式
的通項公式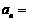 .
.
二.解答題(本大題共6道題,計90分.解答應寫出必要的文字說明、證明過程或演算步驟)
15.在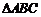 中,角
中,角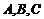 的對邊分別為
的對邊分別為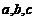 ,且
,且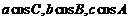 成等差數列.
成等差數列.
⑴求角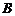 的值;
的值;
⑵若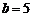 ,求△
,求△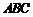 周長的取值范圍.
周長的取值范圍.
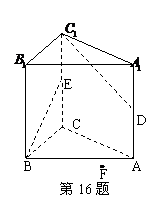 16.已知直三棱柱
16.已知直三棱柱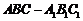 中,
中,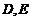 分別為
分別為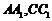 的中點,
的中點,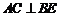 ,點
,點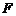 在線段
在線段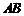 上,且
上,且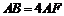 .
.
⑴求證: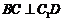 ;
;
⑵若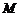 為線段
為線段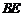 上一點,試確定
上一點,試確定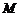 在線段
在線段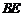 上的位置,
上的位置,
使得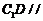 平面
平面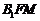 .
.
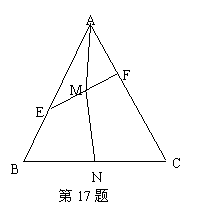 17.如圖,在邊長為1的正三角形
17.如圖,在邊長為1的正三角形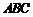 中,
中,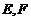 分別是邊
分別是邊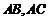 上的點,若
上的點,若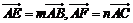 ,
,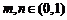 .設
.設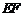 的中點為
的中點為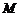 ,
,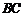 的中點為
的中點為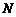 .
.
⑴若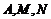 三點共線,求證
三點共線,求證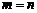 ;
;
⑵若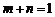 ,求
,求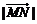 的最小值.
的最小值.
18.已知橢圓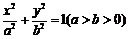 的左、右焦點分別為
的左、右焦點分別為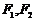 ,其右準線上
,其右準線上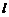 上存在點
上存在點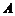 (點
(點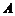 在
在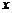 軸上方),使
軸上方),使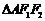 為等腰三角形.
為等腰三角形.
⑴求離心率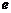 的范圍;
的范圍;
⑵若橢圓上的點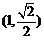 到兩焦點
到兩焦點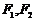 的距離之和為
的距離之和為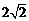 ,求
,求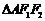 的內切圓的方程.
的內切圓的方程.
19.已知函數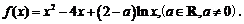
⑴當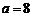 時,求函數
時,求函數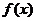 的單調區間;
的單調區間;
⑵求函數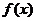 在區間
在區間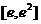 上的最小值.
上的最小值.
20.設數列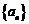 滿足
滿足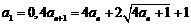 ,令
,令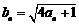 .
.
⑴試判斷數列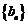 是否為等差數列?并求數列
是否為等差數列?并求數列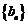 的通項公式;
的通項公式;
⑵令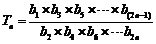 ,是否存在實數
,是否存在實數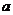 ,使得不等式
,使得不等式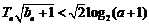 對一切
對一切
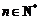 都成立?若存在,求出
都成立?若存在,求出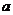 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
⑶比較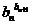 與
與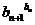 的大小.
的大小.
試題答案
一.填空題
1.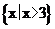 2.
2. 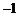 3.
3. 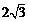 4. 25 5.
4. 25 5. 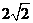 6.
6. 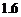
7.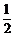 8.
8. 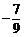 9. 800 10.7 11. a
9. 800 10.7 11. a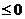 12.
12. 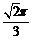 13.
13. 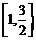 14.
14. 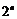
二.解答題
15.⑴因為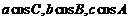 成等差數列,所以
成等差數列,所以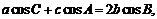 …………2分
…………2分
由正弦定理得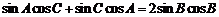 ,即
,即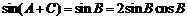 .
.
因為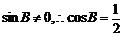 ,又
,又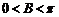 ,所以
,所以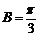 .…………6分
.…………6分
⑵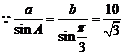 ,
,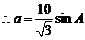 ,同理
,同理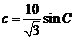 ,…………8分
,…………8分
因為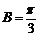 ,所以
,所以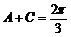 ,
,
所以△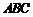 周長
周長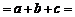
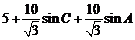
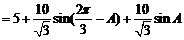
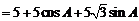
 …………12分
…………12分
因為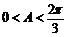 ,所以
,所以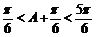 ,所以△
,所以△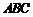 周長的取值范圍為
周長的取值范圍為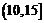 .
…14分
.
…14分
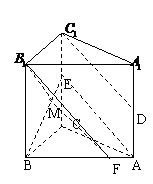 16.⑴由直三棱柱可知
16.⑴由直三棱柱可知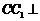 平面
平面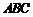 ,所以
,所以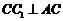 ,…………2分
,…………2分
又因為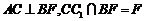 ,
,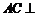 面
面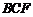 ,
,
故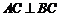 ,
…………4分
,
…………4分
又在直三棱柱中,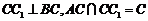 ,
,
故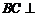 面
面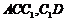 在平面
在平面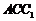 內,所以
內,所以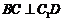 …………6分
…………6分
⑵連結AE,在BE上取點M,使BE=4ME, …………8分
連結FM,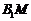 ,F
,F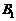 ,在
,在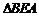 中,由BE=4ME,AB=4AF
中,由BE=4ME,AB=4AF
所以MF//AE, …………12分
又在面AA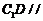 平面
平面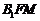 . …………14分
. …………14分
17.⑴由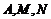 三點共線,得
三點共線,得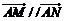 ,
…………………………2分
,
…………………………2分
設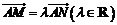 ,即
,即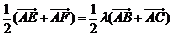 , …………………………4分
, …………………………4分
所以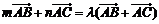 ,所以
,所以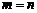 .
…………………………6分
.
…………………………6分
⑵因為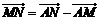 =
=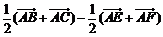
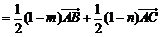 ,
,
又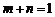 ,所以
,所以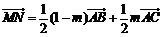 , …………………………10分
, …………………………10分
所以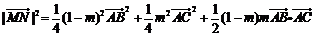
=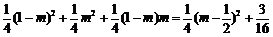
故當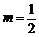 時,
時,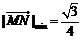 .
…………………………14分
.
…………………………14分
18.⑴由題意有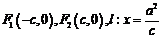 .
…………2分
.
…………2分
設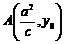 ,由
,由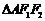 為等腰三角形,則只能是
為等腰三角形,則只能是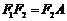 ,又
,又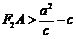 ,
,
即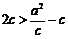 ,所以
,所以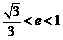 .
…………6分
.
…………6分
⑵由題意得橢圓的方程為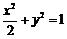 ,其離心率為
,其離心率為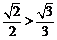 ,此時
,此時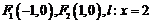 .
.
由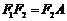 ,可得
,可得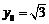 .
…………10分
.
…………10分
設內切圓的圓心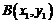 ,
,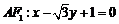 ,
,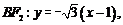
因為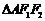 為等腰三角形,所以
為等腰三角形,所以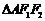 的內切圓的圓心點
的內切圓的圓心點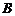 到
到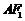 的距離等于點
的距離等于點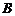 到
到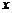 軸的距離,即
軸的距離,即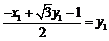 , ①
, ①
由點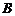 在直線
在直線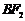 上,所以
上,所以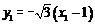 , ②
, ②
由①②可得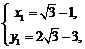
所以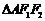 的內切圓的方程為
的內切圓的方程為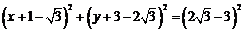 .…………16分
.…………16分
注:本題亦可先用面積求出半徑,再求圓的方程.
19.⑴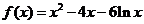 ,
,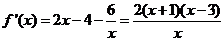 , …………2分
, …………2分
由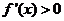 得
得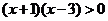 , 解得
, 解得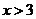 或
或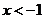 .
.
注意到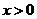 ,所以函數
,所以函數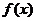 的單調遞增區間是
的單調遞增區間是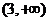 .
.
由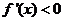 得
得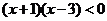 ,解得
,解得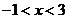 ,
,
注意到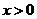 ,所以函數
,所以函數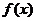 的單調遞減區間是
的單調遞減區間是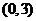 .
.
綜上所述,函數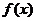 的單調遞增區間是
的單調遞增區間是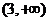 ,單調遞減區間是
,單調遞減區間是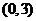 .…………6分
.…………6分
⑵當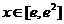 時,
時, 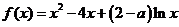 ,所以
,所以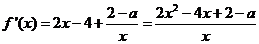 ,
,
設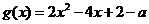 .
.
①當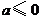 時,有
時,有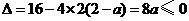 , 此時
, 此時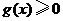 ,所以
,所以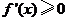 ,
,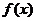 在
在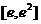 上單調遞增.所以
上單調遞增.所以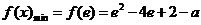 .
…………8分
.
…………8分
②當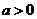 時,
時,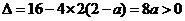 ,
,
令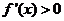 ,即
,即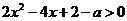 ,解得
,解得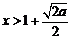 或
或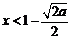 (舍);
(舍);
令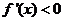 ,即
,即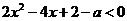 ,解得
,解得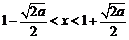 .
.
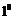 若
若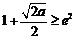 ,即
,即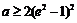 時,
時, 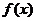 在區間
在區間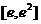 單調遞減,
單調遞減,
所以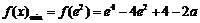 .
.
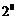 若
若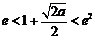 ,即
,即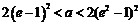 時,
時, 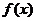 在區間
在區間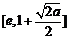 上單調遞減,
上單調遞減,
在區間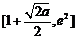 上單調遞增,
上單調遞增,
所以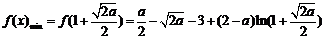 .
.
 若
若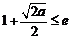 ,即
,即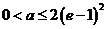 時,
時, 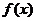 在區間
在區間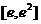 單調遞增,
單調遞增,
所以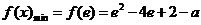 .
…………14分
.
…………14分
綜上所述,當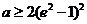 時,
時, 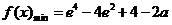 ;
;
當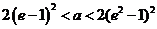 時,
時,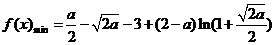 ;
;
當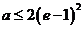 時,
時, 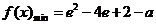 .
…………16分
.
…………16分
20. ⑴由已知得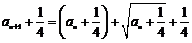 ,
,
即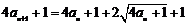 ,
…………2分
,
…………2分
所以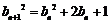 ,即
,即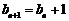 ,
,
又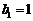 ,所以數列
,所以數列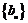 為等差數列,通項公式為
為等差數列,通項公式為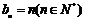 . …………6分
. …………6分
(2)令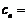
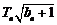 ,由
,由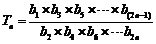 ,得
,得
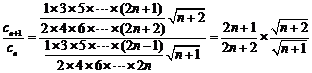
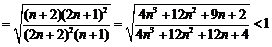
所以,數列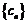 為單調遞減數列,
…………8分
為單調遞減數列,
…………8分
所以數列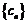 的最大項為
的最大項為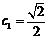 ,
,
若不等式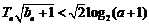 對一切
對一切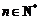 都成立,只需
都成立,只需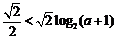 ,解得
,解得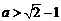 ,
,
又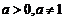 ,所以
,所以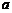 的取值范圍為
的取值范圍為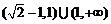 .
…………12分
.
…………12分
(3)問題可轉化為比較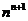 與
與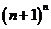 的大小.設函數
的大小.設函數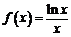 ,所以
,所以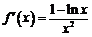 .
.
當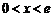 時,
時,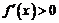 ;當
;當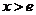 時,
時,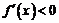 .所以
.所以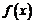 在
在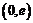 上為增函數;
上為增函數;
在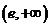 上為減函數.
上為減函數.
當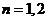 時,顯然有
時,顯然有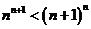 ,
,
當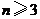 時,
時,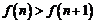 ,即
,即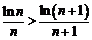 ,所以
,所以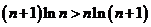 ,
,
即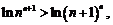 所以
所以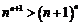 .
.
綜上:當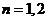 時,
時,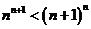 ,即
,即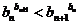 ;
;
當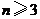 時,
時,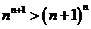 即
即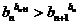 .
…………16分
.
…………16分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com