
題目列表(包括答案和解析)
3.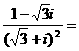 ( )
( )
A.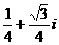 B.
B.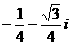 C.
C.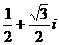 D.
D.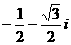
2.拋物線y=ax2 的準線方程是y=2,則a的值為 ( )
A. B.-
B.- C.8 D.-8
C.8 D.-8
一項是符合題目要求的.
1.不等式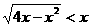 的解集是 ( )
的解集是 ( )
A.(0,2) B.(2,+∞)
C.(2,4) D.(-∞,0)∪(2,+∞)
22.解:(1)設B,C的坐標分別為
B(t,0),C(t-2,0),
則線段BC的中垂線方程為x=t-1, ① 1分
AB中點(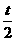 ,
,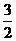 ),AB斜率為
),AB斜率為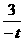 (t≠0),
(t≠0),
所以線段AB的中垂線方程為
y-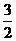 =
=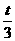 (x-
(x-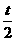 ) ② 3分
) ② 3分
由①②得:x2=6y-8(-2≤x≤2且x≠-1) ③ 5分
當x=-1時,t=0時,三角形外心P為(-1,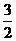 ),適合③;
),適合③;
所以P點的軌跡為x2=6y-8 6分
(2)由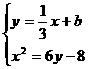 得x2-2x-6b+8=0 ④
得x2-2x-6b+8=0 ④
x1+x2=2,x1x2=8-6b 8分
所以|EF|=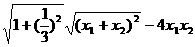 =
=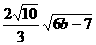 ,
,
又因為d=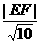 , 11分
, 11分
所以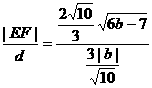 =
=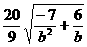
=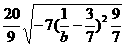 13分
13分
因方程④有兩個不相同的實數根,設f(x)=x2-2x-6b+8
由題意(-2)2-4(8-6b)>0得b>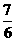 ,∴
,∴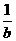 <
<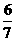 . 13分
. 13分
當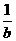 =
=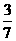 時,即b=
時,即b=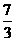 時,(
時,(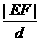 )max=
)max=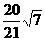 .
.
所以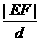 的最大值是
的最大值是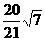 ,此時b=
,此時b=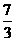 . 14分
. 14分
21.解:(1)設C上任一點P(x,y).
當x≥4時,(x-4)+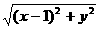 =5,
=5,
整理得y2=-16(x-5)(4≤x≤5). 3分
當x<4時,(4-x)+ 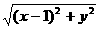 =5,
=5,
整理得y2=4x.(0≤x<4),
所以,y2=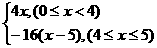 6分
6分
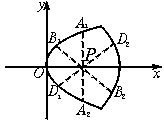
(2)因曲線C關于x軸對稱,所以直線x=3與C的兩個交點A1、A2關于P(3,0)對稱.
由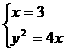 知A1(3,2
知A1(3,2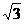 ),A2(3,-2
),A2(3,-2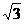 ). 8分
). 8分
又設B1(x1,y1),B2(x2,y2)關于P點對稱,且分別在左右支上,
則由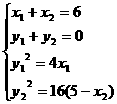 10分
10分
得B1(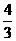 ,
,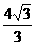 )、B2(
)、B2(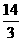 ,-
,-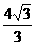 )、D1(
)、D1(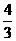 ,-
,-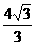 )、D2(
)、D2(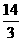 ,
, 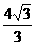 ).
).
共三對. 12分
20.解:設在一個單位重量的新合金中,含第一、第二、第三塊合金重量分別為x、y、z,則含鉻百分比為W=0.4x+0.1y+0.5z. 2分
其中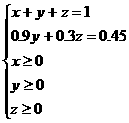 消去z得
消去z得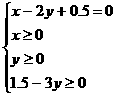
即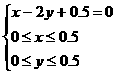 6分
6分
(x,y)對應的點集為線段AB(包括端點)
由于W=0.4x-1.4y+0.75,即y=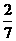 x+
x+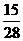 -
-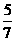 W ①
W ①
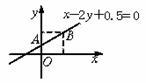
①表示的直線與線段AB有公共點, 10分
由此得直線截距的取值范圍為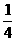 ≤
≤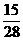 -
-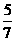 W≤
W≤ ,得0.25≤W≤0.4,
,得0.25≤W≤0.4,
即含鉻的百分比范圍是[0.25,0.4] 12分
19.解:設P1(x1,y1)、P2(x2,y2)
由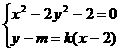 去y得
去y得
(1-2k2)x2-4k(m-2k)x-2[(m-2k)2+1]=0, 4分
依題意P(2,m)是P1P2的中點,
∴x1+x2=4,得km=1,① 6分
又Δ>0,
∴16k2(m-2k)2-4(1-2k2)·(-2)[(m-2k)2+1]>0
2k2(m-2k)2-(2k2-1)[(m-2k)2+1]>0,
(m-2k)2-(2k2-1)>0 8分
由①式有(m-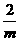 )2-(
)2-(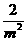 -1)>0,
-1)>0,
m2+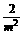 -3>0,(m2-2)(m2-1)>0 10分
-3>0,(m2-2)(m2-1)>0 10分
∴|m|> 或|m|<1,
或|m|<1,
∴m的取值范圍是(-∞,- )∪(-1,1)∪(
)∪(-1,1)∪( ,+∞). 12分
,+∞). 12分
則tanθ=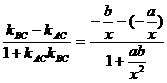 =
=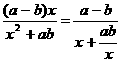 6分
6分
∵a>b,∴tanθ≤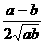 8分
8分
等號當且僅當x=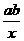 ,即x=
,即x=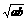 時成立.
時成立.
又θ∈(0,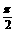 ),所以當x=
),所以當x=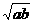 時,θ取最大值arctan
時,θ取最大值arctan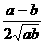 .
.
故C點應在NN上距M為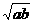 處. 12分
處. 12分
18.解:(1)依題意可設橢圓方程為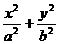 =1(a>b>0),
=1(a>b>0),
直線x-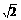 y=0與橢圓交點為N(c,
y=0與橢圓交點為N(c,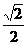 c)(c為橢圓的半焦距), 3分
c)(c為橢圓的半焦距), 3分
則由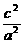 +
+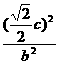 =1,
=1,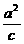 =4
=4 及a2-b2=c2,得a2=16,b2=8,c2=8.
及a2-b2=c2,得a2=16,b2=8,c2=8.
所求橢圓方程為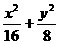 =1. 6分
=1. 6分
(2)易求得直線AB的方程為y=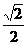 (x+2
(x+2 ), 8分
), 8分
代入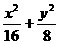 =1,化簡得x2+2
=1,化簡得x2+2 x-4=0, 9分
x-4=0, 9分
由韋達定理及弦長公式得|AB|=6 12分
22.(本小題滿分14分)
在△ABC中,A點的坐標為(0,3),BC邊的長為2,且BC在x軸上滑動.
(1)求△ABC的外心P的軌跡方程;
(2)設一直線l:y=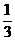 x+b與P的軌跡交于E、F點,原點O到直線l的距離為d,求
x+b與P的軌跡交于E、F點,原點O到直線l的距離為d,求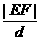 的最大值,并求此時b的值.
的最大值,并求此時b的值.
高三數學(文)全國統一標準測試(三)答案
21.(本小題滿分12分)
已知曲線C滿足:曲線C任意一點到定點A(1,0)與定直線x=4的距離和等于5.
(1)求曲線C的方程;
(2)試判斷曲線C上有幾對不同的點關于定點P(3,0)對稱,并求出這幾對點的坐標.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com