
題目列表(包括答案和解析)
18. (本小題滿分14分)
(本小題滿分14分)
請您設(shè)計(jì)一個(gè)帳篷。它下部的形狀是高為1m的正六
棱柱,上部的形狀是側(cè)棱長為3m的正六棱錐(如右
圖所示)。試問當(dāng)帳篷的頂點(diǎn)O到底面中心 的距離
的距離
為多少時(shí),帳篷的體積最大?
[考點(diǎn)分析:本題主要考查利用導(dǎo)數(shù)研究函數(shù)的最值的基礎(chǔ)知識,以及運(yùn)用數(shù)學(xué)知識解決實(shí)際問題的能力]
解:設(shè)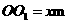 ,則
,則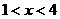 。
。
由題設(shè)可得正六棱錐底面邊長為: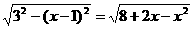 ,(單位:
,(單位: )
)
故底面正六邊形的面積為: =
=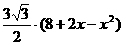 ,(單位:
,(單位: )
)
帳篷的體積為:

 (單位:
(單位: )
)
求導(dǎo)得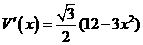 。
。
令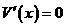 ,解得
,解得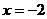 (不合題意,舍去)或
(不合題意,舍去)或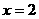 。
。
當(dāng) 時(shí),
時(shí), ,
,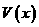 為增函數(shù);
為增函數(shù);
當(dāng)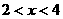 時(shí),
時(shí),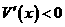 ,
,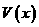 為減函數(shù)。
為減函數(shù)。
∴當(dāng)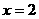 時(shí),
時(shí),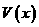 最大。
最大。
答:當(dāng)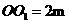 時(shí),帳篷的體積最大,最大體積為
時(shí),帳篷的體積最大,最大體積為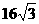
 。
。
17.(本小題滿分12分,第一小問滿分5分,第二小問滿分7分)
已知三點(diǎn)P(5,2)、 (-6,0)、
(-6,0)、 (6,0)。
(6,0)。
(Ⅰ)求以 、
、 為焦點(diǎn)且過點(diǎn)P的橢圓的標(biāo)準(zhǔn)方程;
為焦點(diǎn)且過點(diǎn)P的橢圓的標(biāo)準(zhǔn)方程;
(Ⅱ)設(shè)點(diǎn)P、 、
、 關(guān)于直線y=x的對稱點(diǎn)分別為
關(guān)于直線y=x的對稱點(diǎn)分別為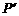 、
、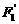 、
、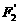 ,求以
,求以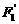 、
、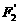 為焦點(diǎn)且過點(diǎn)
為焦點(diǎn)且過點(diǎn)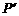 的雙曲線的標(biāo)準(zhǔn)方程。
的雙曲線的標(biāo)準(zhǔn)方程。
[考點(diǎn)分析:本題主要考查橢圓與雙曲線的基本概念、標(biāo)準(zhǔn)方程、幾何性質(zhì)等基礎(chǔ)知識和基本運(yùn)算能力]
[解](I)由題意,可設(shè)所求橢圓的標(biāo)準(zhǔn)方程為 +
+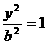
 ,其半焦距
,其半焦距 。
。
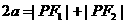
 , ∴
, ∴
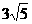 ,
,
 ,故所求橢圓的標(biāo)準(zhǔn)方程為
,故所求橢圓的標(biāo)準(zhǔn)方程為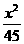 +
+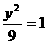 ;
;
(II)點(diǎn)P(5,2)、 (-6,0)、
(-6,0)、 (6,0)關(guān)于直線y=x的對稱點(diǎn)分別為:
(6,0)關(guān)于直線y=x的對稱點(diǎn)分別為:
 、
、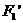 (0,-6)、
(0,-6)、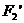 (0,6)
(0,6)
設(shè)所求雙曲線的標(biāo)準(zhǔn)方程為 -
-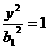
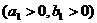 ,由題意知半焦距
,由題意知半焦距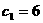 ,
,

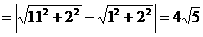 , ∴
, ∴
 ,
,
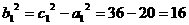 ,故所求雙曲線的標(biāo)準(zhǔn)方程為
,故所求雙曲線的標(biāo)準(zhǔn)方程為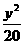 -
- 。
。
(11)在△ABC中,已知BC=12,A=60°,B=45°,則AC= ▲
解:利用正弦定理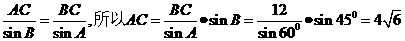
點(diǎn)評:本題主要考查正弦定理的應(yīng)用
(12)設(shè)變量x、y滿足約束條件 ,則
,則 的最大值為 ▲
的最大值為 ▲
解:根據(jù)線性約束條件畫出可行域(圖略),顯然在(3,4)處取得最大值18
點(diǎn)評:本題主要考查線性規(guī)劃的基礎(chǔ)知識。
(13)今有2個(gè)紅球、3個(gè)黃球、4個(gè)白球,同色球不加以區(qū)分,將這9個(gè)球排成一列有 ▲ 種不同的方法(用數(shù)字作答)。
解:由題意,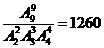
點(diǎn)評:本題主要考查不全相異元素的全排列
(14) = ▲
= ▲
解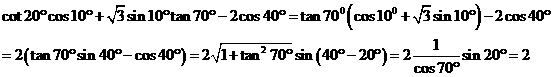
點(diǎn)評:本題主要考查三角函數(shù)的畫簡與求值
(15)對正整數(shù)n,設(shè)曲線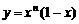 在x=2處的切線與y軸交點(diǎn)的縱坐標(biāo)為
在x=2處的切線與y軸交點(diǎn)的縱坐標(biāo)為 ,則數(shù)列
,則數(shù)列 的前n項(xiàng)和的公式是 ▲
的前n項(xiàng)和的公式是 ▲
解: ,令x=0,求出切線與y軸交點(diǎn)的縱坐標(biāo)為
,令x=0,求出切線與y軸交點(diǎn)的縱坐標(biāo)為 ,所以
,所以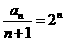 ,則數(shù)列
,則數(shù)列 的前n項(xiàng)和
的前n項(xiàng)和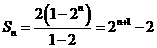
點(diǎn)評:本題主要考查利用導(dǎo)數(shù)求切線方程,再與數(shù)列知識結(jié)合起來,解決相關(guān)問題。
(16)不等式 的解集為 ▲
的解集為 ▲
解:
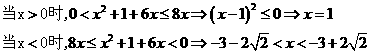
綜上: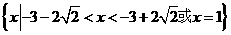
點(diǎn)評:本題主要考查對數(shù)不等式的解法
(1)已知 ,函數(shù)
,函數(shù)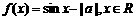 為奇函數(shù),則a=
為奇函數(shù),則a=
(A)0 (B)1 (C)-1 (D)±1
解:法一:由函數(shù)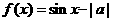 是定義域?yàn)镽的奇函數(shù),則
是定義域?yàn)镽的奇函數(shù),則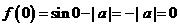 , 即
, 即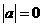 ,則a=0,選A
,則a=0,選A
法二: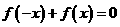 得:
得: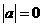 ,則a=0,選A
,則a=0,選A
點(diǎn)評:主要考查奇函數(shù)的定義和性質(zhì)
(2)圓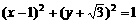 的切線方程中有一個(gè)是
的切線方程中有一個(gè)是
(A)x-y=0 (B)x+y=0 (C)x=0 (D)y=0
解:圓心為(1, ),半徑為1,故此圓必與y軸(x=0)相切,選C
),半徑為1,故此圓必與y軸(x=0)相切,選C
點(diǎn)評:本題主要考查圓的定義及直線與圓的位置關(guān)系
(3)某人5次上班途中所花的時(shí)間(單位:分鐘)分別為x,y,10,11,9.已知這組數(shù)據(jù)的平均數(shù)為10,方差為2,則|x-y|的值為
(A)1 (B)2 (C)3 (D)4
解: 由平均數(shù)公式為10,得 則
則 ;又由于方差為2,則
;又由于方差為2,則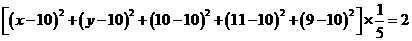 得
得 ,所以有
,所以有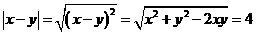 ,故選(D)
,故選(D)
點(diǎn)評:本題主要考查平均數(shù)與方差的定義等統(tǒng)計(jì)方面的基礎(chǔ)知識
(4)為了得到函數(shù)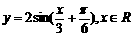 的圖像,只需把函數(shù)
的圖像,只需把函數(shù)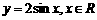 的圖像上所有的點(diǎn)
的圖像上所有的點(diǎn)
(A)向左平移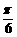 個(gè)單位長度,再把所得各點(diǎn)的橫坐標(biāo)縮短到原來的
個(gè)單位長度,再把所得各點(diǎn)的橫坐標(biāo)縮短到原來的 倍(縱坐標(biāo)不變)
倍(縱坐標(biāo)不變)
(B)向右平移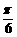 個(gè)單位長度,再把所得各點(diǎn)的橫坐標(biāo)縮短到原來的
個(gè)單位長度,再把所得各點(diǎn)的橫坐標(biāo)縮短到原來的 倍(縱坐標(biāo)不變)
倍(縱坐標(biāo)不變)
(C)向左平移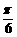 個(gè)單位長度,再把所得各點(diǎn)的橫坐標(biāo)伸長到原來的3倍(縱坐標(biāo)不變)
個(gè)單位長度,再把所得各點(diǎn)的橫坐標(biāo)伸長到原來的3倍(縱坐標(biāo)不變)
(D)向右平移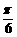 個(gè)單位長度,再把所得各點(diǎn)的橫坐標(biāo)伸長到原來的3倍(縱坐標(biāo)不變)
個(gè)單位長度,再把所得各點(diǎn)的橫坐標(biāo)伸長到原來的3倍(縱坐標(biāo)不變)
解:根據(jù)三角函數(shù)的圖像變換法則易得:把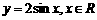 向左平移
向左平移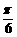 個(gè)單位長度得
個(gè)單位長度得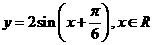 ,再把所得各點(diǎn)的橫坐標(biāo)伸長到原來的3倍(縱坐標(biāo)不變)故選(C)
,再把所得各點(diǎn)的橫坐標(biāo)伸長到原來的3倍(縱坐標(biāo)不變)故選(C)
點(diǎn)評:本題主要考查形如 的三角函數(shù)圖像的變換
的三角函數(shù)圖像的變換
(5) 的展開式中含x的正整數(shù)指數(shù)冪的項(xiàng)數(shù)是
的展開式中含x的正整數(shù)指數(shù)冪的項(xiàng)數(shù)是
(A)0 (B)2 (C)4 (D)6
解:展開式通項(xiàng)為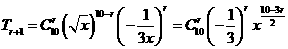 ,若展開式中含x的正整數(shù)指數(shù)冪,即
,若展開式中含x的正整數(shù)指數(shù)冪,即 所以
所以 ,選(B)
,選(B)
點(diǎn)評:本題主要考查二項(xiàng)式定理的相關(guān)知識
(6)已知兩點(diǎn)M(-2,0)、N(2,0),點(diǎn)P為坐標(biāo)平面內(nèi)的動(dòng)點(diǎn),滿足 =0,則動(dòng)點(diǎn)P(x,y)的軌跡方程為
=0,則動(dòng)點(diǎn)P(x,y)的軌跡方程為
(A)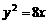 (B)
(B) (C)
(C)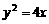 (D)
(D)
解:由題意 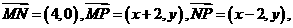

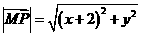 ,所以有
,所以有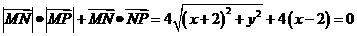
即: ,故選(B)
,故選(B)
點(diǎn)評:本題主要考查點(diǎn)的軌跡方程的求法
(7)若A、B、C為三個(gè)集合,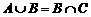 ,則一定有
,則一定有
(A)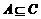 (B)
(B)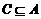 (C)
(C)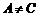 (D)
(D)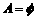
解:由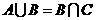 知,
知, ,故選(A)
,故選(A)
點(diǎn)評:本題主要考查集合間關(guān)系的運(yùn)算
(8)設(shè)a、b、c是互不相等的正數(shù),則下列等式中不恒成立的是
(A)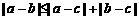 (B)
(B)
(C)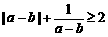 (D)
(D)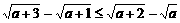
解:因?yàn)?sub>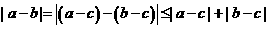 ,所以(A)恒成立;
,所以(A)恒成立;
在(B)兩側(cè)同時(shí)乘以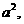 得
得
 所以(B)恒成立;
所以(B)恒成立;
(C)中,當(dāng)a>b時(shí),恒成立,a<b時(shí),不成立;
(D)中,分子有理化得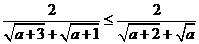 恒成立,故選(C)
恒成立,故選(C)
點(diǎn)評:本題主要考查不等式的相關(guān)知識
|
|
|
|
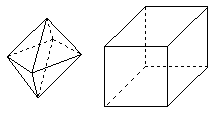 (9)兩相同的正四棱錐組成如圖1所示的幾何體,可放棱長為1的正方體內(nèi),使正四棱錐的底面ABCD與正方體的某一個(gè)平面平行,且各頂點(diǎn)均在正方體的面上,則這樣的幾何體體積的可能值有
(9)兩相同的正四棱錐組成如圖1所示的幾何體,可放棱長為1的正方體內(nèi),使正四棱錐的底面ABCD與正方體的某一個(gè)平面平行,且各頂點(diǎn)均在正方體的面上,則這樣的幾何體體積的可能值有
|
(C)3個(gè) (D)無窮多個(gè)
解:法一:本題可以轉(zhuǎn)化為一個(gè)正方形可以有多少個(gè)內(nèi)接正方形,顯然有無窮多個(gè)
法二:通過計(jì)算,顯然兩個(gè)正四棱錐的高均為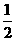 ,考查放入正方體后,面ABCD所在的截面,顯然其面積是不固定的,取值范圍是
,考查放入正方體后,面ABCD所在的截面,顯然其面積是不固定的,取值范圍是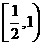 ,所以該幾何體的體積取值范圍是
,所以該幾何體的體積取值范圍是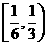
點(diǎn)評:本題主要考查學(xué)生能否迅速構(gòu)造出一些常見的幾何模型,并不是以計(jì)算為主
 (10)右圖中有一個(gè)信號源和五個(gè)接收器。接收器與信號源在同一個(gè)串聯(lián)線路中時(shí),就能接收到信號,否則就不能接收到信號。若將圖中左端的六個(gè)接線點(diǎn)隨機(jī)地平均分成三組,將右端的六個(gè)接線點(diǎn)也隨機(jī)地平均分成三組,再把所有六組中每組的兩個(gè)接線點(diǎn)用導(dǎo)線連接,則這五個(gè)接收器能同時(shí)接收到信號的概率是
(10)右圖中有一個(gè)信號源和五個(gè)接收器。接收器與信號源在同一個(gè)串聯(lián)線路中時(shí),就能接收到信號,否則就不能接收到信號。若將圖中左端的六個(gè)接線點(diǎn)隨機(jī)地平均分成三組,將右端的六個(gè)接線點(diǎn)也隨機(jī)地平均分成三組,再把所有六組中每組的兩個(gè)接線點(diǎn)用導(dǎo)線連接,則這五個(gè)接收器能同時(shí)接收到信號的概率是
(A) (B)
(B)
(C) (D)
(D)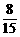
解:由題意,左端的六個(gè)接線點(diǎn)隨機(jī)地平均分成三組有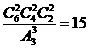 種分法,同理右端的六個(gè)接線點(diǎn)也隨機(jī)地平均分成三組有
種分法,同理右端的六個(gè)接線點(diǎn)也隨機(jī)地平均分成三組有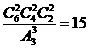 種分法;要五個(gè)接收器能同時(shí)接收到信號,則需五個(gè)接收器與信號源串聯(lián)在同一個(gè)線路中,即五個(gè)接收器的一個(gè)全排列,再將排列后的第一個(gè)元素與信號源左端連接,最后一個(gè)元素與信號源右端連接,所以符合條件的連接方式共有
種分法;要五個(gè)接收器能同時(shí)接收到信號,則需五個(gè)接收器與信號源串聯(lián)在同一個(gè)線路中,即五個(gè)接收器的一個(gè)全排列,再將排列后的第一個(gè)元素與信號源左端連接,最后一個(gè)元素與信號源右端連接,所以符合條件的連接方式共有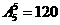 種,所求的概率是
種,所求的概率是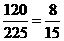 ,故選(D)
,故選(D)
點(diǎn)評:本題要求學(xué)生能夠熟練運(yùn)用排列組合知識解決計(jì)數(shù)問題,并進(jìn)一步求得概率問題,其中隱含著平均分組問題。
21. (本小題滿分14分)
已知橢圓C1: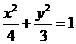 ,拋物線C2:
,拋物線C2: ,且C1、C2的公共弦AB過橢圓C1的右焦點(diǎn).
,且C1、C2的公共弦AB過橢圓C1的右焦點(diǎn).
(Ⅰ)當(dāng)AB⊥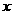 軸時(shí),求
軸時(shí),求 、
、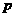 的值,并判斷拋物線C2的焦點(diǎn)是否在直線AB上;
的值,并判斷拋物線C2的焦點(diǎn)是否在直線AB上;
(Ⅱ)是否存在 、
、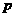 的值,使拋物線C2的焦點(diǎn)恰在直線AB上?若存在,求出符合條件的
的值,使拋物線C2的焦點(diǎn)恰在直線AB上?若存在,求出符合條件的 、
、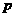 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
2006年普通高等學(xué)校招生全國統(tǒng)一考試(湖南卷)
20. (本小題滿分14分)
對1個(gè)單位質(zhì)量的含污物體進(jìn)行清洗,清洗前其清潔度(含污物體的清潔度定義為: )為0.8,要求洗完后的清潔度是0.99.有兩種方案可供選擇,方案甲:一次清洗;方案乙:兩次清洗.該物體初次清洗后受殘留水等因素影響,其質(zhì)量變?yōu)?sub>
)為0.8,要求洗完后的清潔度是0.99.有兩種方案可供選擇,方案甲:一次清洗;方案乙:兩次清洗.該物體初次清洗后受殘留水等因素影響,其質(zhì)量變?yōu)?sub> (1≤a≤3).設(shè)用
(1≤a≤3).設(shè)用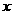 單位質(zhì)量的水初次清洗后的清潔度是
單位質(zhì)量的水初次清洗后的清潔度是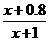 (
(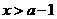 ),用
),用 質(zhì)量的水第二次清洗后的清潔度是
質(zhì)量的水第二次清洗后的清潔度是 ,其中
,其中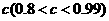 是該物體初次清洗后的清潔度.
是該物體初次清洗后的清潔度.
(Ⅰ)分別求出方案甲以及 時(shí)方案乙的用水量,并比較哪一種方案用水量較少;
時(shí)方案乙的用水量,并比較哪一種方案用水量較少;
(Ⅱ)若采用方案乙,當(dāng) 為某定值時(shí),如何安排初次與第二次清洗的用水量,使總用水量最少?并討論
為某定值時(shí),如何安排初次與第二次清洗的用水量,使總用水量最少?并討論 取不同數(shù)值時(shí)對最少總用水量多少的影響.
取不同數(shù)值時(shí)對最少總用水量多少的影響.
19. (本小題滿分14分)
已知函數(shù) ,數(shù)列{
,數(shù)列{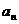 }滿足:
}滿足:
證明:(ⅰ) ;(ⅱ)
;(ⅱ)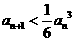 .
.
18. (本小題滿分14分)
如圖4,已知兩個(gè)正四棱錐P-ABCD與Q-ABCD的高分別為1和2,AB=4.
(Ⅰ)證明PQ⊥平面ABCD;
(Ⅱ)求異面直線AQ與PB所成的角;
 (Ⅲ)求點(diǎn)P到平面QAD的距離.
(Ⅲ)求點(diǎn)P到平面QAD的距離.
17.(本小題滿分12分)
某安全生產(chǎn)監(jiān)督部門對5家小型煤礦進(jìn)行安全檢查(簡稱安檢).若安檢不合格,則必須進(jìn)行整改.若整改后經(jīng)復(fù)查仍不合格,則強(qiáng)行關(guān)閉.設(shè)每家煤礦安檢是否合格是相互獨(dú)立的,且每家煤礦整改前安檢合格的概率是0.5, 整改后安檢合格的概率是0.8,計(jì)算(結(jié)果精確到0.01):
(Ⅰ)恰好有兩家煤礦必須整改的概率;
 (Ⅱ)平均有多少家煤礦必須整改;
(Ⅱ)平均有多少家煤礦必須整改;
(Ⅲ)至少關(guān)閉一家煤礦的概率.
16. (本小題滿分12分)
(本小題滿分12分)
如圖3,D是直角△ABC斜邊BC上一點(diǎn),AB=AD,記∠CAD=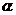 ,∠ABC=
,∠ABC=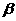 .
.
(Ⅰ)證明  ;
;
(Ⅱ)若AC= DC,求
DC,求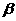 的值.
的值.
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com