
題目列表(包括答案和解析)
4.若將函數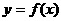 圖象按向量
圖象按向量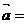 (
(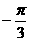 ,
,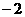 )平移后,得到函數
)平移后,得到函數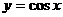 的圖象,則原圖象的函數解析式是:
的圖象,則原圖象的函數解析式是:
A.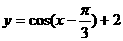 B.
B.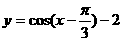
C.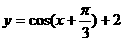 D.
D.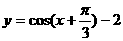
3.直線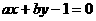 在
在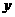 軸上的截距為1,且它的傾斜角是直線
軸上的截距為1,且它的傾斜角是直線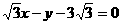 的傾斜角的2倍,則
的傾斜角的2倍,則
A.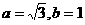 B.
B. 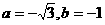 C.
C. 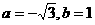 D.
D. 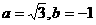
2.已知函數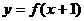 的圖象過點(3,2),則函數
的圖象過點(3,2),則函數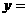
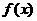 的圖象關于
的圖象關于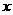 軸的對稱圖形一定過點
軸的對稱圖形一定過點
A. (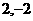 ) B.
) B.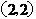 C. (
C. (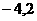 ) D. (
) D. (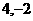 )
)
1.等比數列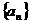 中,
中,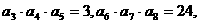 則
則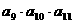 的值為
的值為
A.48 B.72 C.144 D.192
(15)(本小題滿分14分)
解關于x的不等式
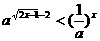 ,(a>0且a≠1)。
,(a>0且a≠1)。
(16)(本小題滿分14分)
已知:定義在R上的函數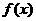 為奇函數,且在
為奇函數,且在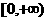 上是增函數。
上是增函數。
(Ⅰ)求證: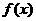 在
在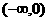 上也是增函數;
上也是增函數;
(Ⅱ)對任意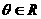 ,求實數m,使不等式
,求實數m,使不等式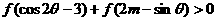 恒成立。
恒成立。
(17)(本小題滿分14分)
在長方體ABCD-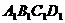 中,AB=2,
中,AB=2,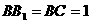 ,E為
,E為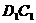 的中點,連結ED,EC,EB和DB。
的中點,連結ED,EC,EB和DB。
(Ⅰ)求證:平面EDB⊥平面EBC;
(Ⅱ)求二面角E-DB-C的正切值;
(Ⅲ)求異面直線EB和DC的距離。
(18)(本小題滿分14分)
某造紙廠擬建一座平面圖形為矩形且面積為200平方米的二級污水處理池(平面圖如圖所示),池的深度一定,池的外圈周壁建造單價為每米400元,中間一條隔壁建造單價為每米100元,池底建造單價每平方米60元(池壁厚度忽略不計)。
(Ⅰ)設污水處理池的長為x米時,寫出總造價f(x)的解析式;
(Ⅱ)污水處理池的長設計為多少米時,可使總造價最低。

(19)(本小題滿分14分)
已知橢圓c: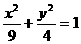 ,將橢圓c平移,中心移到點(1,2),成為橢圓c’。
,將橢圓c平移,中心移到點(1,2),成為橢圓c’。
(Ⅰ)求橢圓c’的方程;
(Ⅱ)橢圓c’上存在關于直線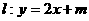 對稱的不同的兩點,求出m的范圍。
對稱的不同的兩點,求出m的范圍。
(20)(本小題滿分14分)
已知函數 ,滿足條件:
,滿足條件:
①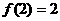 ;②
;②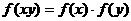 ;③
;③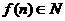 ;
;
④當x>y時,有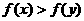 。
。
(Ⅰ)求f(1),f(3)的值;
(Ⅱ)由f(1),f(2),f(3)的值,猜想f(n)的解析式;
(Ⅲ)證明你猜想的f(n)的解析式的正確性。
(11)已知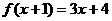 ,則
,則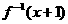 =________________。
=________________。
(12)在一個棱長為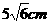 的正四面體內有一點P,它到三個面的距離分別是1cm,2cm,3cm,則它到第四個面的距離為_______________cm。
的正四面體內有一點P,它到三個面的距離分別是1cm,2cm,3cm,則它到第四個面的距離為_______________cm。
(13)設等比數列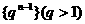 的前n項和為
的前n項和為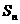 ,前n+1項的和為
,前n+1項的和為 ,則
,則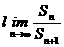 =___________________。
=___________________。
(14)拋物線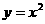 和圓
和圓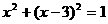 上最近兩點的距離是_________________。
上最近兩點的距離是_________________。
(1)設集合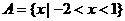
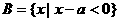 ,若
,若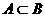 ,則a的取值范圍是( )
,則a的取值范圍是( )
(A)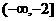 (B)
(B)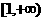 (C)
(C)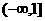 (D)
(D)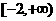
(2)已知二面角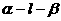 ,直線
,直線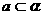 ,
,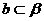 ,且a與l不垂直,b與l不垂直,那么( )
,且a與l不垂直,b與l不垂直,那么( )
(A)a與b可能垂直,但不可能平行 (B)a與b可能垂直,也可能平行
(C)a與b不可能垂直,但可能平行 (D)a與b不可能垂直,也不可能平行
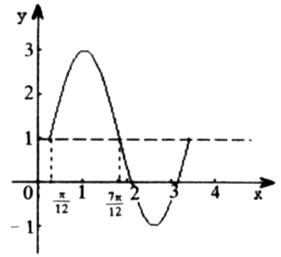
(3)函數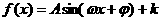 在一個周期內的圖象如圖所示,函數
在一個周期內的圖象如圖所示,函數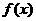 解析式為( )
解析式為( )
(A)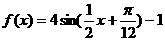
(B)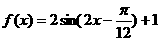
(C)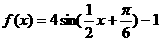
(D)
(4)若橢圓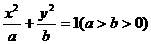 ,雙曲線
,雙曲線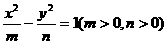 有相同的焦點
有相同的焦點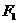 ,
,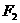 ,P是兩曲線的交點,則
,P是兩曲線的交點,則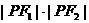 的值是( )
的值是( )
(A) (B)
(B)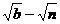 (C)a-m (D)b-n
(C)a-m (D)b-n
(5)如圖,O為直二面角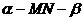 的棱MN上的一點,射線OE,OF分別在
的棱MN上的一點,射線OE,OF分別在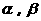 內,且∠EON=∠FON=45°,則∠EOF的大小為( )
內,且∠EON=∠FON=45°,則∠EOF的大小為( )
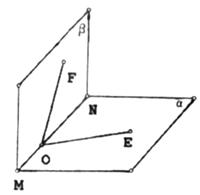
(A)30° (B)45° (C)60° (D)90°
(6)在等差數列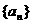 中,
中, 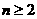 ,公差d<0,前n項和是
,公差d<0,前n項和是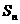 ,則有( )
,則有( )
(A)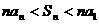 (B)
(B)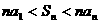
(C)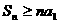 (D)
(D)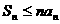
(7)8種不同的商品,選出5種放入5個不同的柜臺中,如果甲、乙兩種商品不能放入第5號柜臺中,那么不同的放法共有( )
(A)3360種 (B)5040種 (C)5880種 (D)2160種
(8)下列四個命題:
①滿足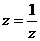 的復數只有
的復數只有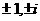 ;
;
②若a,b是兩個相等的實數,則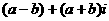 是純虛數;
是純虛數;
③復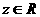 的充要條件是
的充要條件是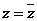 ;
;
④復平面內x軸即實軸,y軸即虛軸。
其中正確的有( )
(A)1個 (B)2個 (C)3個 (D)4個
(9)在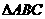 中,
中,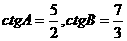 ,則角C等于( )
,則角C等于( )
(A)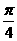 (B)
(B)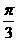
(C)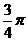 (D)
(D)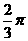
(10)過拋物線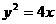 的焦點作直線與此拋物線交于P,Q兩點,那么線段PQ中點的軌跡方程是( )
的焦點作直線與此拋物線交于P,Q兩點,那么線段PQ中點的軌跡方程是( )
(A)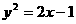 (B)
(B)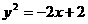
(C)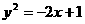 (D)
(D)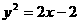
第Ⅱ卷(非選擇題共100分)
20.(本小題滿分12分)
已知定義域為[0,1]的函數f(x)同時滿足:
(1)對于任意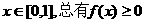 ;
;
(2)f(1)=1
(3)若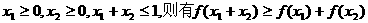
(Ⅰ)試求f(0)的值;
(Ⅱ)試求函數f(x)的最大值;
(Ⅲ)(理科學生做,文科學生不做)
試證明:滿足上述條件的函數f(x)對一切實數x,都有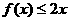 .
.
19.(本小題滿分16分)
在直角坐標平面內,已知兩點A(-2,0)及B(2,0),動點Q到點A的距離為6,線段BQ的垂直平分線交AQ于點P.
(Ⅰ)證明|PA|+|PB|為常數,并寫出點P的軌跡T的方程;
(Ⅱ)(理科學生做)過點B的直線l與曲線T相交于M、N兩點,線段MN的中點R與點S(-1,0)的連線的縱截距為t,試求t的取值范圍.
 (文科學生做)過點B且傾斜角為120°的直線l與曲線T相交于M、N兩點,試求△AMN的面積.
(文科學生做)過點B且傾斜角為120°的直線l與曲線T相交于M、N兩點,試求△AMN的面積.
18.(本小題12分)
有一組數據: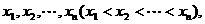 它們的算術平均值為10,若去掉其中最大的一個,余下的數據的算術平均值為9;若去掉其中最小的一個,余下數據的算術平均值為11.
它們的算術平均值為10,若去掉其中最大的一個,余下的數據的算術平均值為9;若去掉其中最小的一個,余下數據的算術平均值為11.
(Ⅰ)求出第一個數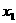 關于n的表達式及第n個數
關于n的表達式及第n個數 關于n的表達式.
關于n的表達式.
(Ⅱ)若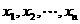 都是正整數,試求第n個數
都是正整數,試求第n個數 的最大值,并舉出滿足題目要求且
的最大值,并舉出滿足題目要求且 取到最大值的一組數據.
取到最大值的一組數據.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com