
題目列表(包括答案和解析)
5.在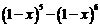 的展開式中,含
的展開式中,含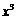 的項的系數是(
)
的項的系數是(
)
(A)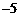 (B) 5 (C)
(B) 5 (C) 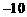 (D)
10
(D)
10
解: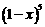 中x3的系數為10,
中x3的系數為10,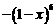 中x3的系數為-20,∴
中x3的系數為-20,∴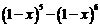 的展開式中x3的系數為-10,選(C)
的展開式中x3的系數為-10,選(C)
4.設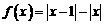 ,則
,則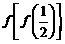 =( )
=( )
(A) 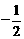 (B)0 (C)
(B)0 (C)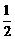 (D)
1
(D)
1
解: =
=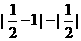 =0,
=0, 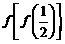 =f(0)=1,選(D)
=f(0)=1,選(D)
3.點 到直線
到直線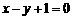 的距離是( )
的距離是( )
(A)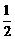 (B)
(B)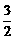 (C)
(C)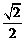 (D)
(D)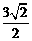
解:點 到直線
到直線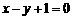 的距離d=
的距離d=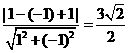 ,選(D)
,選(D)
2.設全集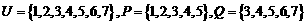 ,則
,則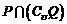 =( )
=( )
(A) 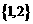 (B)
(B) 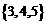 (C)
(C) 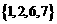 (D)
(D)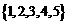
解: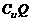 ={1,2,},故
={1,2,},故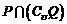 ={1,2},選(A)
={1,2},選(A)
1.函數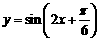 的最小正周期是(
)
的最小正周期是(
)
(A) 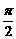 (B)
(B) 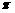 (C)
(C) 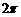 (D)
(D) 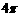
解:T=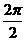 =π,選(B)
=π,選(B)
(17)(本小題滿分12分)
已知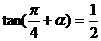
(1)求 的值;(2)求
的值;(2)求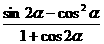 的值。
的值。
(18)(本小題滿分12分)
從4名男生和2名女生中任選3人參加演講比賽。
(1)求所選3人都是男生的概率;
(2)求所選3人中恰有1名女生的概率;
(3)求所選3人中至少有1名女生的概率。
(19)(本小題滿分12分)
如圖,在四棱錐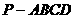 中,底面ABCD是正方形,側棱
中,底面ABCD是正方形,側棱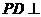 底面ABCD,
底面ABCD,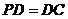 ,
,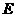 是PC的中點。
是PC的中點。
(1)證明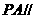 平面EDB;(2)求EB與底面ABCD所成的角的正切值。
平面EDB;(2)求EB與底面ABCD所成的角的正切值。
(20)(本小題滿分12分)
設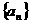 是一個公差為
是一個公差為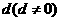 的等差數列,它的前10項和
的等差數列,它的前10項和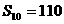 且
且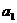 ,
,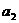 ,
,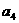 成等比數列。
成等比數列。
(1)證明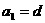 ;(2)求公差
;(2)求公差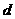 的值和數列
的值和數列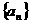 的通項公式。
的通項公式。
(21)(本小題滿分12分)
已知函數 是R上的奇函數,當
是R上的奇函數,當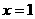 時
時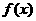 取得極值
取得極值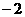 。
。
(1)求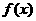 的單調區間和極大值;
的單調區間和極大值;
(2)證明對任意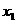 ,
,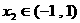 ,不等式
,不等式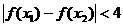 恒成立。
恒成立。
(22)(本小題滿分14分)
橢圓的中心是原點O,它的短軸長為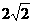 ,相應于焦點
,相應于焦點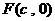
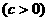 的準線
的準線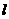 與
與 軸相交于點A,
軸相交于點A,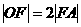 ,過點A的直線與橢圓相交于P、Q兩點。
,過點A的直線與橢圓相交于P、Q兩點。
(1)求橢圓的方程及離心率;(2)若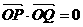 ,求直線PQ的方程。
,求直線PQ的方程。
2004年普通高等學校招生全國統一考試(天津卷)
(13)
某工廠生產A、B、C三種不同型號的產品。產品數量之比依次為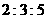 。現用分層抽樣方法抽出一個容量為
。現用分層抽樣方法抽出一個容量為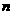 的樣本,樣本中A種型號產品有16件。那么此樣本的容量
的樣本,樣本中A種型號產品有16件。那么此樣本的容量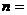 。
。
(14)
已知向量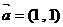 ,
,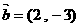 ,若
,若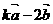 與
與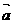 垂直,則實數
垂直,則實數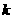 等于
。
等于
。
(15)
如果過兩點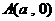 和
和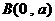 的直線與拋物線
的直線與拋物線 沒有交點,那么實數
沒有交點,那么實數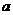 的取值范圍是
。
的取值范圍是
。
(16) 從0,1,2,3,4,5中任取3個數字,組成沒有重復數字的三位數,其中能被5整除的三位數共有 個。(用數字作答)
(1)
設集合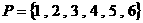 ,
,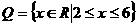 ,那么下列結論正確的是
,那么下列結論正確的是
(A)
 (B)
(B)
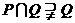
(C)
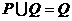 (D)
(D)
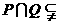
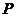
(2)
不等式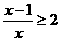 的解集為
的解集為
(A)
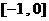 (B)
(B)
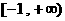
(C)
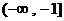 (D)
(D)

(3) 對任意實數a、b、c,在下列命題中,真命題是
(A)“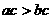 ”是“
”是“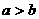 ”的必要條件
”的必要條件
(B)“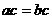 ”是“
”是“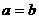 ”的必要條件
”的必要條件
(C)“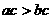 ”是“
”是“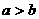 ”的充分條件
”的充分條件
(D)“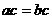 ”是“
”是“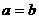 ”的充分條件
”的充分條件
(4)
若平面向量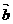 與向量
與向量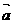
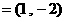 的夾角是
的夾角是 ,且
,且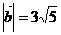 ,則
,則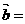
(A)
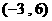 (B)
(B)
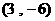 (C)
(C)
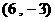 (D)
(D)
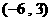
(5)
設P是雙曲線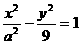 上一點,雙曲線的一條漸近線方程為
上一點,雙曲線的一條漸近線方程為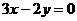 ,
,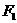 、
、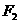 分別是雙曲線的左、右焦點。若
分別是雙曲線的左、右焦點。若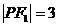 ,則
,則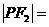
(A) 1或5 (B) 6 (C) 7 (D) 9
(6)
若函數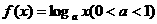 在區間
在區間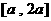 上的最大值是最小值的3倍,則
上的最大值是最小值的3倍,則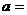
(A)
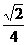 (B)
(B)
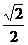 (C)
(C)
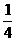 (D)
(D)
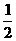
(7)
若過定點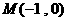 且斜率為
且斜率為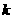 的直線與圓
的直線與圓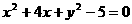 在第一象限內的部分有交點,則
在第一象限內的部分有交點,則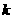 的取值范圍是
的取值范圍是
(A)
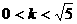 (B)
(B)
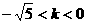
(C)
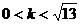 (D)
(D)
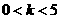
(8)
如圖,定點A和B都在平面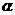 內,定點
內,定點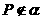 ,
,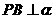 ,C是
,C是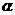 內異于A和B的動點,且
內異于A和B的動點,且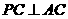 。那么,動點C在平面
。那么,動點C在平面 內的軌跡是
內的軌跡是

(A) 一條線段,但要去掉兩個點 (B) 一個圓,但要去掉兩個點
(C) 一個橢圓,但要去掉兩個點 (D) 半圓,但要去掉兩個點
(9)
函數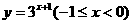 的反函數是
的反函數是
(A)
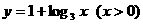 (B)
(B)
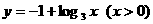
(C)
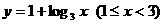 (D)
(D)
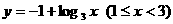
(10)
函數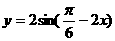
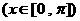 為增函數的區間是
為增函數的區間是
(A)
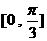 (B)
(B)
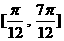 (C)
(C)
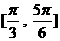 (D)
(D)
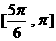
(11) 如圖,在長方體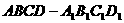 中,
中,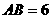 ,
,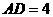 ,
,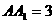 。分別過BC、
。分別過BC、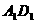 的兩個平行截面將長方體分成三部分,其體積分別記為
的兩個平行截面將長方體分成三部分,其體積分別記為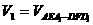 ,
,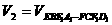 ,
,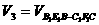 。若
。若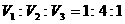 ,則截面
,則截面 的面積為
的面積為
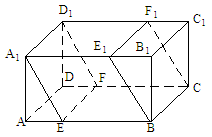
(A)
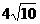 (B)
(B)
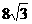 (C)
(C)
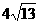 (D)
(D)
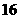
(12)
定義在R上的函數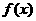 既是偶函數又是周期函數。若
既是偶函數又是周期函數。若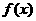 的最小正周期是
的最小正周期是 ,且當
,且當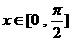 時,
時,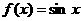 ,則
,則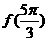 的值為
的值為
(A)
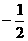 (B)
(B)
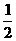 (C)
(C)
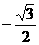 (D)
(D)
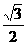
普通高等學校招生全國統一考試
數學(文史類)
第Ⅱ卷(非選擇題 共90分)
(17)(本小題滿分13分)
甲、乙、丙三人在同一辦公室工作。辦公室只有一部電話機,設經過該機打進的電話是打給甲、乙、丙的概率依次為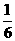 、
、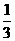 、
、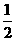 。若在一段時間內打進三個電話,且各個電話相互獨立。求:
。若在一段時間內打進三個電話,且各個電話相互獨立。求:
(Ⅰ)這三個電話是打給同一個人的概率;
(Ⅱ)這三個電話中恰有兩個是打給甲的概率;
(18)(本小題滿分13分)
設函數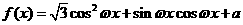 (其中
(其中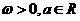 )。且
)。且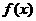 的圖像在
的圖像在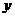 軸右側的第一個最高點的橫坐標是
軸右側的第一個最高點的橫坐標是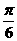 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)如果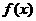 在區間
在區間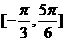 上的最小值為
上的最小值為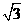 ,求
,求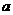 的值;
的值;
(19)(本小題滿分12分)
設函數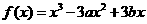 的圖像與直線
的圖像與直線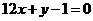 相切于點
相切于點 。
。
(Ⅰ)求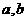 的值;
的值;
(Ⅱ)討論函數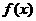 的單調性。
的單調性。
(20)(本小題滿分12分)
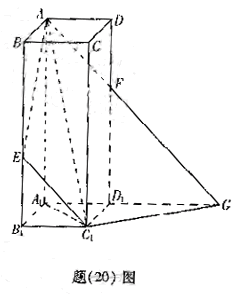 如圖,在增四棱柱
如圖,在增四棱柱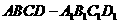 中,
中,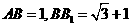 ,
,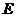 為
為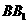 上使
上使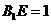 的點。平面
的點。平面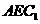 交
交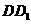 于
于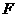 ,交
,交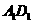 的延長線于
的延長線于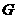 ,求:
,求:
(Ⅰ)異面直線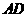 與
與 所成角的大小;
所成角的大小;
(Ⅱ)二面角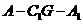 的正切值;
的正切值;
(21)(本小題滿分12分)
已知定義域為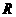 的函數
的函數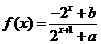 是奇函數。
是奇函數。
(Ⅰ)求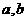 的值;
的值;
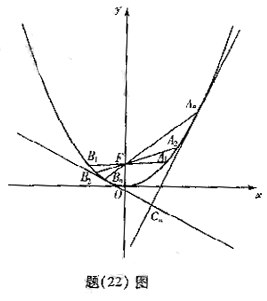
(Ⅱ)若對任意的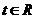 ,不等式
,不等式 恒成立,求
恒成立,求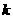 的取值范圍;
的取值范圍;
(22)(本小題滿分12分)
 如圖,對每個正整數
如圖,對每個正整數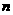 ,
,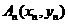 是拋物線
是拋物線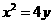 上的點,過焦點
上的點,過焦點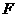 的直線
的直線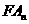 角拋物線于另一點
角拋物線于另一點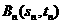 。
。
(Ⅰ)試證: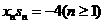 ;
;
(Ⅱ)取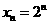 ,并記
,并記 為拋物線上分別以
為拋物線上分別以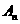 與
與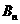 為切點的兩條切線的交點。試證:
為切點的兩條切線的交點。試證: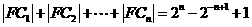 ;
;
(13)已知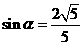 ,
,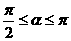 ,則
,則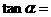 。
。
(14)在數列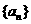 中,若
中,若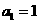 ,
,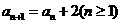 ,則該數列的通項
,則該數列的通項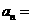 。
。
(15)設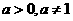 ,函數
,函數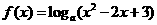 有最小值,則不等式
有最小值,則不等式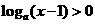 的解集為
。
的解集為
。
(16)已知變量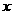 ,
,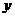 滿足約束條件
滿足約束條件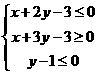 。若目標函數
。若目標函數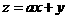 (其中
(其中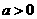 )僅在點
)僅在點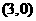 處取得最大值,則
處取得最大值,則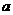 的取值范圍為
。
的取值范圍為
。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com