
題目列表(包括答案和解析)
6.已知 均為銳角,若
均為銳角,若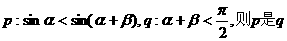 的 ( )
的 ( )
A.充分而不必要條件 B.必要而不充分條件
C.充要條件 D.既不充分也不必要條件
解:∵由 、
、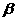 均為銳角,
均為銳角,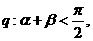 得0<α<α+β<
得0<α<α+β<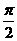 ∴sin(α+β)>sinα,但
∴sin(α+β)>sinα,但 、
、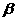 均為銳角,sinα<sin(α+β),不一定能推出α+β<
均為銳角,sinα<sin(α+β),不一定能推出α+β<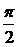 ,如α=
,如α=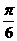 ,β=
,β=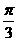 就是一個反例,選(C)
就是一個反例,選(C)
5.不等式組 的解集為 ( )
的解集為 ( )
A.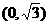 B.
B.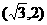 C.
C.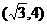 D.
D.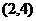
解∵|x-2|<2的解集為(0,4),log2(x2-1)>1的解集為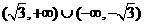 ,∴不等式組
,∴不等式組 的解集
的解集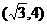 ,選(C)
,選(C)
4.設向量a=(-1,2),b=(2,-1),則(a·b)(a+b)等于 ( )
A.(1,1) B.(-4,-4) C.-4 D.(-2,-2)
解:(a·b)(a+b)=[-2+(-2)](1,1)=(-4,-4),選(B)
3.若函數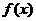 是定義在R上的偶函數,在
是定義在R上的偶函數,在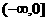 上是減函數,且
上是減函數,且 ,則使得
,則使得
 的取值范圍是 ( )
的取值范圍是 ( )
A. B.
B.
C. D.(-2,2)
D.(-2,2)
解:∵函數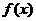 是定義在R上的偶函數,在
是定義在R上的偶函數,在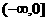 上是減函數,且
上是減函數,且 ,∴f(-2)=0, 在
,∴f(-2)=0, 在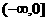 上
上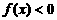 的x的取值范圍是
的x的取值范圍是 ,又由對稱性
,又由對稱性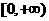 ,∴在R上fx)<0仰x的取值范圍為(-2,2),選(D)
,∴在R上fx)<0仰x的取值范圍為(-2,2),選(D)
2.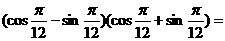 ( )
( )
A.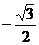 B.
B.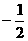 C.
C.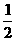 D.
D.
解: ,選(D)
,選(D)
1.圓 關于原點(0,0)對稱的圓的方程為 ( )
關于原點(0,0)對稱的圓的方程為 ( )
A. B.
B.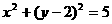
C. D.
D.
解:∵圓 的圓心(-2,0)關于原點對稱的點為(2,0),∴圓
的圓心(-2,0)關于原點對稱的點為(2,0),∴圓 關于原點對稱的圓為(x-2)2+y2=5,選(A).
關于原點對稱的圓為(x-2)2+y2=5,選(A).
22.(本小題12分)
(Ⅰ)證明:(1)當n=2時, ,不等式成立.
,不等式成立.
(2)假設當 時不等式成立,即
時不等式成立,即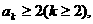
那么 . 這就是說,當
. 這就是說,當 時不等式成立.
時不等式成立.
根據(1)、(2)可知: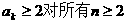 成立.
成立.
(Ⅱ)證法一:
由遞推公式及(Ⅰ)的結論有

兩邊取對數并利用已知不等式得
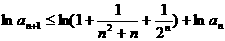
 故
故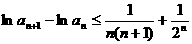
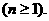
上式從1到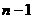 求和可得
求和可得


即
(Ⅱ)證法二:
由數學歸納法易證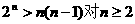 成立,故
成立,故

令
取對數并利用已知不等式得 

上式從2到n求和得 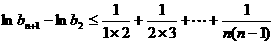

因
故 成立.
成立.
21.(本小題12分)
解:(Ⅰ)設雙曲線C2的方程為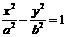 ,則
,則
故C2的方程為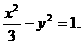
(II)將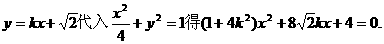
由直線l與橢圓C1恒有兩個不同的交點得
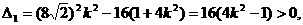
即 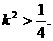 ①
①
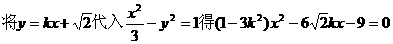 .
.
由直線l與雙曲線C2恒有兩個不同的交點A,B得


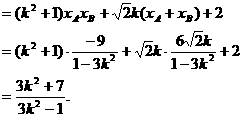
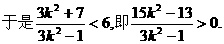 解此不等式得
解此不等式得
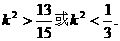 ③
③
由①、②、③得

故k的取值范圍為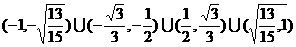
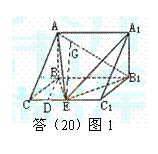
20.(本小題13分)
解法一:
(Ⅰ)因AB⊥面BB1C1C,故AB⊥BE.
又EB1⊥EA,且EA在面BCC1B1內的射影為EB.
由三垂線定理的逆定理知EB1⊥BE,因此BE是異面直線
AB與EB1的公垂線,
在平行四邊形BCC1B1中,設EB=x,則EB1=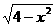 ,
,
作BD⊥CC1,交CC1于D,則BD=BC·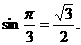
在△BEB1中,由面積關系得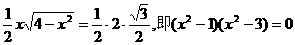 .
.
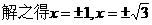 (負根舍去)
(負根舍去)

解之得CE=2,故此時E與C1重合,由題意舍去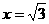 .
.
因此x=1,即異面直線AB與EB1的距離為1.
(Ⅱ)過E作EG//B1A1,則GE⊥面BCC1B,故GE⊥EB1且GE在圓A1B1E內,
又已知AE⊥EB1
故∠AEG是二面角A-EB1-A1的平面角.
因EG//B1A1//BA,∠AEG=∠BAE,故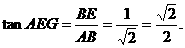
解法二:
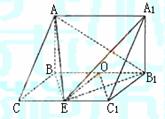 (Ⅰ)
(Ⅰ)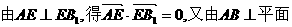
而BB1C1C得AB⊥EB1從而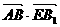 =0.
=0.
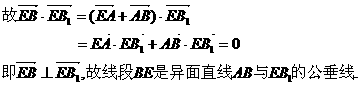
設O是BB1的中點,連接EO及OC1,則在Rt△BEB1中,EO=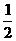 BB1=OB1=1,
BB1=OB1=1,
因為在△OB1C1中,B1C1=1,∠OB1C1=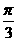 ,故△OB1C1是正三角形,
,故△OB1C1是正三角形,
所以OC1=OB1=1,
又因∠OC1E=∠B1C1C-∠B1C1O=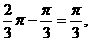 故△OC1E是正三角形,
故△OC1E是正三角形,
所以C1E=1,故CE=1,易見△BCE是正三角形,從面BE=1,
即異面直線AB與EB1的距離是1.
(Ⅱ)由(I)可得∠AEB是二面角A-EB1-B的平面角,在Rt△ABE中,由AB=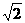 ,
,
BE=1,得tanAEB=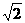 .
.
又由已知得平面A1B1E⊥平面BB1C1C,
故二面角A-EB1-A1的平面角 ,故
,故

解法三:
(I)以B為原點, 、
、 分別為y、z軸建立空間直角坐標系.
分別為y、z軸建立空間直角坐標系.
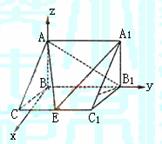 由于BC=1,BB1=2,AB=
由于BC=1,BB1=2,AB=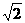 ,∠BCC1=
,∠BCC1=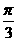 ,
,
在三棱柱ABC-A1B1C1中有
B(0,0,0),A(0,0,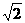 ),B1(0,2,0),
),B1(0,2,0),
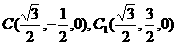
設

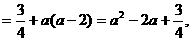
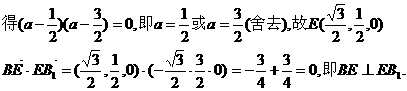
又AB⊥面BCC1B1,故AB⊥BE. 因此BE是異面直線AB、EB1的公垂線,
則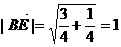 ,故異面直線AB、EB1的距離為1.
,故異面直線AB、EB1的距離為1.
(II)由已知有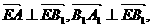 故二面角A-EB1-A1的平面角
故二面角A-EB1-A1的平面角 的大小為向量
的大小為向量
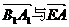 的夾角.
的夾角.

19.(本小題13分)

(1)當
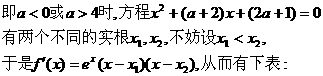
|
x |
 |
x1 |
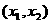 |
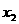 |
 |
 |
+ |
0 |
- |
0 |
+ |
 |
 |
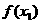 為極大值 為極大值 |
 |
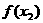 為極小值 為極小值 |
 |
即此時 有兩個極值點.
有兩個極值點.
(2)當 有兩個相同的實根
有兩個相同的實根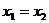
于是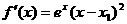
 無極值.
無極值.
(3)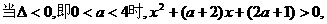
 為增函數,此時
為增函數,此時 無極值. 因此當
無極值. 因此當 無極值點.
無極值點.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com