
3.設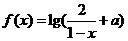 是奇函數,則使
是奇函數,則使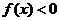 的
的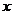 的取值范圍是 x>1或x<0
的取值范圍是 x>1或x<0
2.設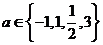 ,則使函數
,則使函數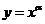 的定義域為R且為奇函數的所有
的定義域為R且為奇函數的所有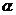 值為 -1,3
值為 -1,3
1.設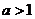 ,函數
,函數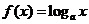 在區間
在區間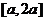 上的最大值與最小值之差為
上的最大值與最小值之差為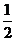 ,則
,則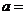 2
2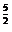
10、冪函數
例10.已知點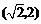 在冪函數
在冪函數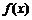 的圖象上,點
的圖象上,點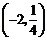 在指數函數
在指數函數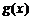 的圖象上.f(x)=x
的圖象上.f(x)=x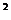
問當x為何值時有:(1)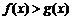 ;(2)
;(2)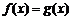 ;(3)
;(3) .g(x)=2
.g(x)=2
分析:由冪函數的定義,先求出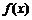 與
與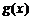 的解析式,再利用圖象判斷即可.
的解析式,再利用圖象判斷即可.
實戰訓練
9、對數函數
例9:已知函數 ,
, ,且
,且
(1)
求函數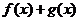 定義域
(-1,1)
定義域
(-1,1)
(2)
判斷函數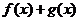 的奇偶性,并說明理由. 偶
的奇偶性,并說明理由. 偶
變式:已知 是
是 上的減函數,那么
上的減函數,那么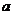 的取值范圍是
的取值范圍是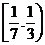
8、指數函數
例8:已知下列等式,比較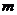 ,
, 的大小:(1)
的大小:(1)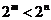 m<n (2)
m<n (2)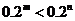 m>n
m>n
變式:函數 在[0,1]上的最大值與最小值的和為3,則
在[0,1]上的最大值與最小值的和為3,則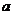 的值為-2或4
的值為-2或4
7.恒成立問題
例7:當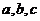 具有什么關系時,二次函數
具有什么關系時,二次函數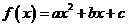 的函數值恒大于零?恒小于零?
的函數值恒大于零?恒小于零?
變式1:已知函數 f (x) = lg (a x 2 + 2x + 1) .
(I)若函數 f (x) 的定義域為 R,求實數 a 的取值范圍; a>1
(II)若函數 f (x) 的值域為 R,求實數 a 的取值范圍. [0,1]
6.值域
例6:求二次函數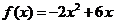 在下列定義域上的值域:
在下列定義域上的值域:
(1)定義域為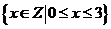 ;(2) 定義域為
;(2) 定義域為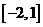 .
.
{0,4} [-20,4]
變式1:函數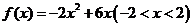 的值域是
的值域是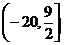
變式2:函數y=cos2x+sinx的值域是[-2,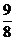 ].
].
5.奇偶性
例5:已知函數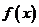 是定義在R上的奇函數,當
是定義在R上的奇函數,當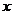 ≥0時,
≥0時,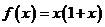 .畫出函數
.畫出函數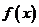 的圖像,并求出函數的解析式.x<0,f(x)= x(1-x)
的圖像,并求出函數的解析式.x<0,f(x)= x(1-x)
變式1:若函數 是偶函數,則在區間
是偶函數,則在區間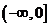 上
上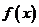 是 增 函數
是 增 函數
4.最值
例4已知函數 在區間[0,m]上有最大值3,最小值2,則m的取值范圍是 [1,2]
在區間[0,m]上有最大值3,最小值2,則m的取值范圍是 [1,2]
變式1:已知函數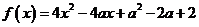 在區間[0,2]上的最小值為3,求a的值.1-
在區間[0,2]上的最小值為3,求a的值.1-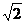 ,
,
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com