
題目列表(包括答案和解析)
4.
若xÎ[-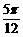 ,-
,-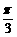 ],則y= tan(x+
],則y= tan(x+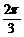 )-tan(x+
)-tan(x+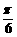 )+cos(x+
)+cos(x+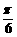 )的最大值是
(A)
)的最大值是
(A)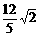 (B)
(B) (C)
(C)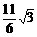 (D)
(D)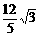
3.
過拋物線y2=8(x+2)的焦點F作傾斜角為60°的直線.若此直線與拋物線交于A,B兩點,弦AB的中垂線與x軸交于P點,則線段PF的長等于
(A)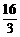 (B)
(B)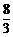 (C)
(C) (D)8
(D)8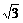
2. 設a, bÎR, ab≠0,那么,直線
ax-y+b=0和曲線 bx2+ay2=ab 的圖形是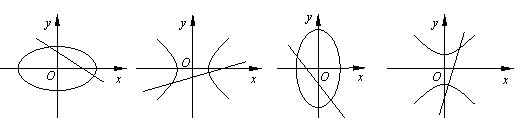
 (A)
(B)
(C) (D)
(A)
(B)
(C) (D)
1. 刪去正整數數列1,2,3,……中的所有完全平方數,得到一個新數列.這個新數列的第2003項是 (A)2046 (B)2047 (C)2048 (D)2049
(17)(本小題滿分12分)
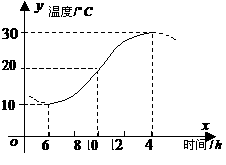
如圖,某地一天從6時至14時的溫度變化曲線近似滿足函數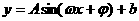 。
。
(Ⅰ)求這段時間的最大溫差;
(Ⅱ)寫出這段曲線的函數解析式。
(18)(本小題滿分12分)
甲、乙兩物體分別從相距70 的兩處同時運動。甲第1分鐘走2
的兩處同時運動。甲第1分鐘走2 ,以后每分鐘比前1分鐘多走1
,以后每分鐘比前1分鐘多走1 ,乙每分鐘走5
,乙每分鐘走5 。
。
(Ⅰ)甲、乙開始運動后幾分鐘相遇?
(Ⅱ)如果甲、乙到達對方起點后立即折反,甲繼續每分鐘比前1分鐘多走1 ,乙繼續每分鐘走5
,乙繼續每分鐘走5 ,那么開始運動幾分鐘后第二次相遇?
,那么開始運動幾分鐘后第二次相遇?
(19)(本小題滿分12分)
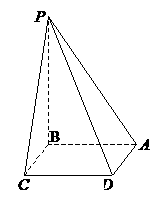
四棱錐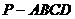 的底面是邊長為
的底面是邊長為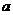 的正方形,
的正方形,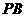
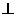 面
面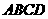 。
。
(Ⅰ)若面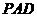 與面
與面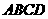 所成的二面角為
所成的二面角為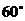 ,求這個四棱錐的體積;
,求這個四棱錐的體積;
(Ⅱ)證明無論四棱錐的高怎樣變化,面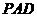 與面
與面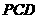 所成的二面角恒大于
所成的二面角恒大于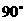 。
。
(20)(本小題滿分12分)
設函數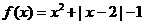 ,
,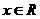 。
。
(Ⅰ)判斷函數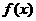 的奇偶性;
的奇偶性;
(Ⅱ)求函數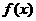 的最小值。
的最小值。
(21)(本小題滿分14分)
已知點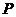 到兩個定點
到兩個定點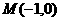 、
、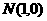 距離的比為
距離的比為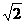 ,點
,點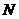 到直線
到直線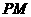 的距離為1。求直線
的距離為1。求直線 的方程。
的方程。
(22)(本小題滿分12分,附加題滿分4分)
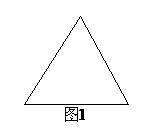
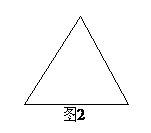
(Ⅰ)給出兩塊相同的正三角形紙片(如圖1,圖2),要求用其中一塊剪拼成一個正三棱錐模型,另一塊剪拼成一個正三棱柱模型,使它們的全面積都與原三角形的面積相等,請設計一種剪拼方法,分別用虛線標示在圖1、圖2中,并作簡要說明;
(Ⅱ)試比較你剪拼的正三棱錐與正三棱柱的體積的大小;
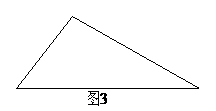
(Ⅲ)(本小題為附加題,如果解答正確,加4分,但全卷總分不超過150分。)
如果給出的是一塊任意三角形的紙片(如圖3),要求剪拼成直三棱柱模型,使它的全面積與給出的三角形的面積相等,請設計一種剪拼方法,用虛線標示在圖3中,并作簡要說明。
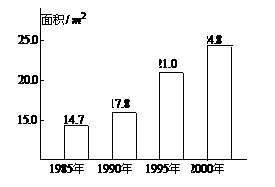
(13)。據新華社2002年3月12日電,1985年到2000年間,我國農村人均居住面積如圖所示,其中,從 年到 年的五年間增長最快。
(14)函數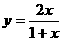
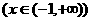 圖象與其反函數圖象的交點坐標為 。
圖象與其反函數圖象的交點坐標為 。
(15)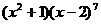 的展開式中
的展開式中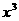 項的系數是
。
項的系數是
。
(16)對于頂點在在原點的拋物線,給出下列條件:
1焦點在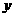 軸上;2焦點在
軸上;2焦點在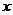 軸上;3拋物線上橫坐標為1的點到焦點的距離為
軸上;3拋物線上橫坐標為1的點到焦點的距離為 ;
;
4拋物線的通徑的長為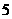 ;5由原點向過焦點的某條直線作垂線,垂足坐標為
;5由原點向過焦點的某條直線作垂線,垂足坐標為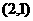 。
。
能使這拋物線方程為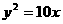 的條件是 。(要求填寫合適條件的序號)
的條件是 。(要求填寫合適條件的序號)
(1)若直線 與圓
與圓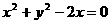 相切,則
相切,則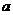 的值為
的值為
(A)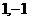 (B)
(B)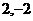 (C)
(C)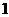 (D)
(D)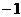
(2)復數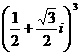 的值是
的值是
(A)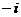 (B)
(B)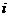 (C)
(C)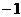 (D)
(D)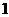
(3)不等式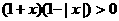 的解集是
的解集是
(A)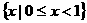 (B)
(B)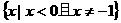 (C)
(C)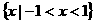 (D)
(D)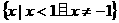
(4)函數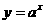 在
在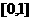 上的最大值與最小值的和為3,則
上的最大值與最小值的和為3,則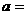
(A)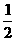 (B)
(B)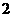 (C)
(C)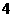 (D)
(D)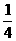
(5)在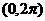 內,使
內,使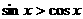 成立的
成立的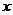 取值范圍為
取值范圍為
(A)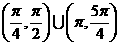 (B)
(B)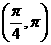 (C)
(C)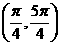 (D)
(D)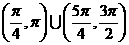
(6)設集合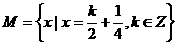 ,
,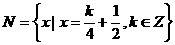 ,則
,則
(A)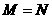 (B)
(B)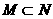 (C)
(C)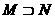 (D)
(D)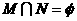
(7)橢圓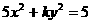 的一個焦點是
的一個焦點是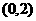 ,那么
,那么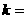
(A)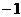 (B)
(B)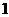 (C)
(C)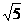 (D)
(D)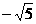
(8)一個圓錐和一個半球有公共底面,如果圓錐的體積恰好與半球的體積相等,那么這個圓錐截面頂角的余弦值是
(A)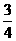 (B)
(B) (C)
(C)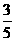 (D)
(D)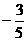
(9)已知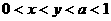 ,則有
,則有
(A)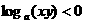 (B)
(B)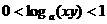 (C)
(C)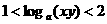 (D)
(D)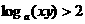
(10)函數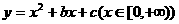 是單調函數的充要條件是
是單調函數的充要條件是
(A) (B)
(B)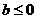 (C)
(C)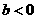 (D)
(D)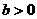
(11)設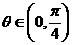 ,則二次曲線
,則二次曲線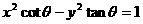 的離心率的取值范圍為
的離心率的取值范圍為
(A)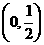 (B)
(B)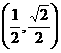 (C)
(C)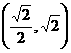 (D)
(D)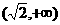
(12)從正方體的6個面中選取3個面,其中有2個面不相鄰的選法共有
(A)8種(B)12種(C)16種(D)20種
(17)(本小題滿分12分)
已知 ,
,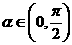 。求
。求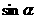 、
、 的值。
的值。
(18)(本小題滿分12分)
如圖,正方形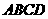 、
、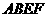 的邊長都是1,而且平面
的邊長都是1,而且平面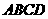 、
、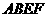 互相垂直。點
互相垂直。點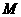
在 上移動,點
上移動,點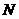 在
在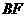 上移動,若
上移動,若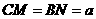
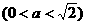 。
。
(Ⅰ)求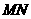 的長;
的長;
(Ⅱ)當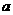 為何值時,
為何值時,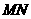 的長最小;
的長最小;
(Ⅲ)當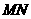 長最小時,求面
長最小時,求面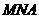 與面
與面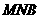 所成的二面角
所成的二面角 的大小。
的大小。
(19)(本小題滿分12分)
設點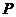 到點
到點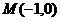 、
、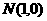 距離之差為
距離之差為 ,到
,到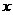 軸、
軸、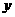 軸距離之比為
軸距離之比為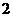 。
。
求 的取值范圍。
的取值范圍。
(20)(本小題滿分12分)
某城市2001年末汽車保有量為30萬輛,預計此后每年報廢上一年末汽車保有量的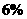 ,并且每年新增汽車數量相同。為保護城市環境,要求該城市汽車保有量不超過
,并且每年新增汽車數量相同。為保護城市環境,要求該城市汽車保有量不超過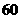 萬量,那么每年新增汽車數量不應超過多少輛?
萬量,那么每年新增汽車數量不應超過多少輛?
(21)(本小題滿分12分)
設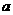 為實數,函數
為實數,函數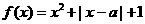 ,
,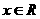 。
。
(Ⅰ)討論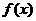 的奇偶性;
的奇偶性;
(Ⅱ)求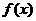 的最小值。
的最小值。
(22)(本小題滿分14分)
設數列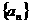 滿足
滿足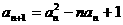 ,
,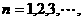
(Ⅰ)當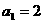 時,求
時,求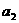 ,
,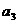 ,
,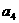 ,并由此猜想出
,并由此猜想出 的一個通項公式;
的一個通項公式;
(Ⅱ)當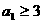 時,證明對所有的
時,證明對所有的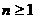 ,有
,有
(ⅰ)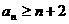 ;
;
(ⅱ)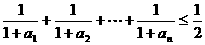 。
。
(13)函數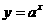 在
在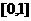 上的最大值與最小值的和為3,則
上的最大值與最小值的和為3,則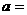 。
。
(14)橢圓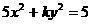 的一個焦點是
的一個焦點是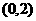 ,那么
,那么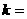 。
。
(15)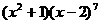 的展開式中
的展開式中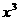 項的系數是
。
項的系數是
。
(16)已知函數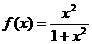 ,那么
,那么
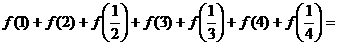 。
。
(1)圓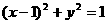 的圓心到直線
的圓心到直線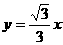 的距離是
的距離是
(A)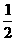 (B)
(B)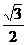 (C)
(C)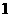 (D)
(D)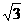
(2)復數 的值是
的值是
(A)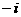 (B)
(B)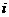 (C)
(C)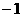 (D)
(D)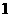
(3)不等式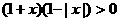 的解集是
的解集是
(A)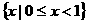 (B)
(B)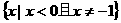 (C)
(C)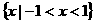 (D)
(D)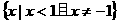
(4)在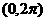 內,使
內,使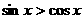 成立的
成立的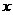 取值范圍為
取值范圍為
(A)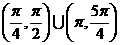 (B)
(B)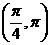 (C)
(C)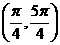 (D)
(D)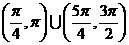
(5)設集合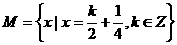 ,
,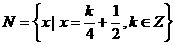 ,則
,則
(A)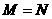 (B)
(B)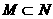 (C)
(C)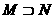 (D)
(D)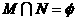
(6)點 到曲線
到曲線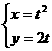 (其中參數
(其中參數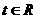 )上的點的最短距離為
)上的點的最短距離為
(A) (B)
(B)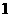 (C)
(C)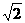 (D)
(D)
(7)一個圓錐和一個半球有公共底面,如果圓錐的體積恰好與半球的體積相等,那么這個圓錐截面頂角的余弦值是
(A)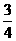 (B)
(B)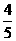 (C)
(C)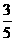 (D)
(D)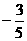
(8)正六棱柱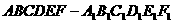 的底面邊長為
的底面邊長為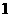 ,側棱長為
,側棱長為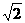 ,則這個棱柱的側面對角線
,則這個棱柱的側面對角線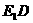 與
與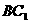 所成的角是
所成的角是
(A)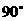 (B)
(B)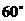 (C)
(C)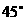 (D)
(D)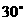
(9)函數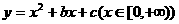 是單調函數的充要條件是
是單調函數的充要條件是
(A)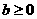 (B)
(B)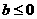 (C)
(C)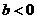 (D)
(D)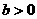
(10)函數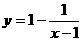 的圖象是
的圖象是
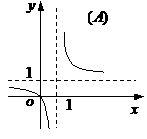
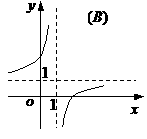
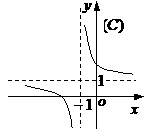
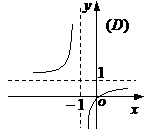
(11)從正方體的6個面中選取3個面,其中有2個面不相鄰的選法共有
(A)8種(B)12種(C)16種(D)20種
(12)據2002年3月5日九屆人大五次會議《政府工作報告》:“2001年國內生產總值達到95 933億元,比上年增長7.3%.”如果“十·五”期間(2001年-2005年)每年的國內生產總值都按此年增長率增長,那么到“十·五”末我國國內年生產總值約為
(A)115 000億元(B)120 000億元(C)127 000億元(D)135 000億元
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com