
題目列表(包括答案和解析)
4.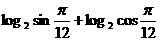 的值為 ( )
的值為 ( )
A.4 B.-4 C.2 D.-2
3.過點A(-1,2)作直線,若直線在兩條坐標軸上的截距相等,則滿足條件的直線有( )
A.1條 B.2條 C.3條 D.4條
2.設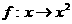 是集合A到集合B的映射,如果B={1,2},則A∩B一定是 ( )
是集合A到集合B的映射,如果B={1,2},則A∩B一定是 ( )
A.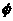 B.
B.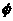 或{1} C.{1} D.
或{1} C.{1} D.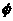 或{2}
或{2}
1.條件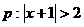 ,條件
,條件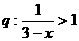 ,則
,則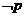 是
是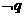 的 ( )
的 ( )
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既不充分又不必要條件
演算步驟。
(17)(本小題滿分12分)
已知函數(shù)
 ,
,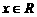 。
。
(I)當函數(shù)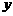 取得最大值時,求自變量
取得最大值時,求自變量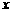 的集合;
的集合;
(II)該函數(shù)的圖象可由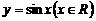 的圖象經(jīng)過怎樣的平移和伸縮變換
的圖象經(jīng)過怎樣的平移和伸縮變換
得到?
(18)(本小題12分)
設{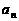 }為等比數(shù)列,
}為等比數(shù)列,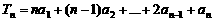 ,已知
,已知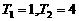
(Ⅰ)求數(shù)列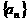 的首項和公式比;
的首項和公式比;
(Ⅱ)求數(shù)列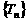 的通項公式。
的通項公式。
(19)(本小題滿分12分)
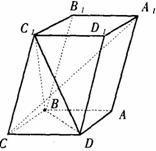 如圖,已知平行六面體ABCD-
如圖,已知平行六面體ABCD-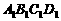 的底面ABCD是菱形,且
的底面ABCD是菱形,且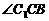 =
=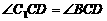 。
。
(I)證明: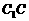 ⊥BD;
⊥BD;
(II)當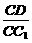 的值為多少時,能使
的值為多少時,能使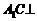 平面
平面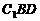 ?請給出證明。
?請給出證明。
(20)(本小題滿分12分)
設函數(shù)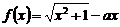 ,其中
,其中 。
。
 (I)解不等式
(I)解不等式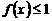 ;
;
(II)證明:當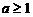 時,函數(shù)
時,函數(shù)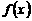 在區(qū)間
在區(qū)間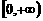 上是單調(diào)函數(shù)。
上是單調(diào)函數(shù)。
(21)(本小題滿分12分)
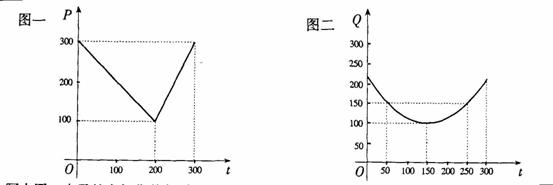
某蔬菜基地種植西紅柿,由歷年市場行情得知,從二月一日起的300天內(nèi),西紅柿市場售價與上市時間的關系用圖一的一條折線表示;西紅柿的種植成本與上市時間的關系用圖二的拋物線段表示。
(I)
寫出圖一表示的市場售價與時間的函數(shù)關系式P=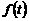 ;
;
寫出圖二表示的種植成本與時間的函數(shù)關系式Q=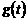 ;
;
(II) 認定市場售價減去種植成本為純收益,問何時上市的西紅柿收益最
大?
(注:市場售價和種植成本的單位:元/ kg,時間單位:天)
kg,時間單位:天)
(22)(本小題滿分14分)
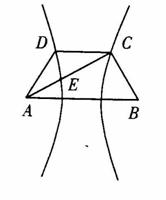 如圖,已知梯形ABCD中
如圖,已知梯形ABCD中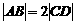 ,點E分有向線段
,點E分有向線段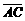 所成的比為
所成的比為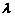 ,雙曲線過C、D、E三點,且以A、B為焦點。當
,雙曲線過C、D、E三點,且以A、B為焦點。當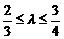 時,求雙曲線離心率
時,求雙曲線離心率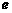 的取值范圍。
的取值范圍。
線上。
(13)乒乓球隊的10名隊員中有3名主力隊員,派5名參加比賽。3名主力
隊員要安排在第一、三、五位置,其余7名隊員選2名安排在第二、四
位置,那么不同的出場安排共有_____種(用數(shù)字作答)。
(14)橢圓 的焦點為
的焦點為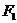 、
、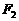 ,點P為其上的動點,當
,點P為其上的動點,當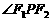 為鈍角
為鈍角
時,點P橫坐標的取值范圍是________。
(15)設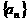 是首項為1的正項數(shù)列,且
是首項為1的正項數(shù)列,且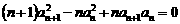 (
(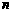 =1,2,
=1,2,
3,…),則它的通項公式是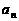 =________。
=________。
(16)如圖,E、F分別為正方體的面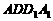 、面
、面 的中心,則四邊形
的中心,則四邊形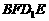 在該正方體的面上的射影可能是_______。(要求:把可能的圖的 序號都填上)
在該正方體的面上的射影可能是_______。(要求:把可能的圖的 序號都填上)
四個選項中,只有一項是符合題目要求的。
(1)
已知集合A=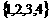 ,那么A的真子集的個數(shù)是
,那么A的真子集的個數(shù)是
(A)3 (B)16 (C)15 (D)4
(2)
在復平面內(nèi),把復數(shù)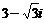 對應的向量按順時針方向旋轉
對應的向量按順時針方向旋轉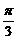 ,所得向量對應的復數(shù)是
,所得向量對應的復數(shù)是
(A)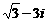 (B)
(B) (C)2
(C)2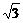 (D)3
(D)3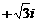
(3)
一個長方體共一項點的三個面的面積分別是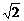 ,
,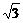 ,
,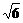 ,這個長方體
,這個長方體
對角線的長是
(A)6 (B)3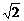 (C)2
(C)2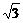 (D)
(D)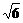
(4)已知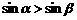 ,那么下列命題成立的是
,那么下列命題成立的是
(A)若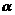 、
、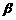 是第三象限角,則
是第三象限角,則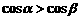
(B)若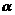 、
、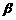 是第二象限角,則
是第二象限角,則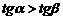
(C)若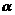 、
、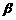 是第三象限角,則
是第三象限角,則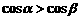
(D)若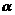 、
、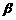 是第四象限角,則
是第四象限角,則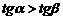
(5)函數(shù)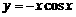 的部分圖象是
的部分圖象是

(6)依法納稅是公民的義務。按規(guī)定,全月工資、薪金所得不超過 800元的部分不必納稅,超過800元的部分,按下列分段累進計算稅款:
|
工資、薪金所得超過800元的部分中 |
稅率 |
|
不超過500元的部分 |
5% |
|
超過500元至2000元的部分 |
10% |
|
超過2000元至5000元的部分 |
15% |
|
… |
… |
某人一月份應交納此項稅款26.78元,則他的當月工資、薪金所得介于
(A) 1200~1500元 (B)900~1200元
(C)800~900元 (D)1500~2800元
(7)若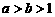 ,P=
,P=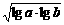 ,Q=
,Q=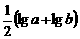 ,R=
,R=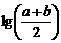 ,則
,則
(A)Q  P
P R
(B)P
R
(B)P Q
Q  R
R
(C)R P
P Q
(D)P
Q
(D)P  R
R Q
Q
(8)以極坐標系中的點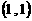 為圓心,1為半徑的圓的方程是
為圓心,1為半徑的圓的方程是
(A) (B)
(B)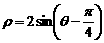
(C)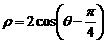 (D)
(D)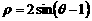
(9)一個圓柱的側面展開圖是一個正方形,這個圓柱的全面積與側面積的比
是
(A) (B)
(B)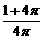 (C)
(C)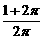 (D)
(D)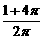
(10)過原點的直線與圓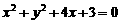 相切,若切點在第三象限,則該直
相切,若切點在第三象限,則該直
線的方程是
(A)y=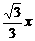 (B)
(B)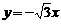 (C)
(C)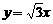 (D)
(D)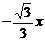
(11)過拋物線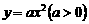 的焦點F作一條直線交拋物線于P、Q兩點,若線
的焦點F作一條直線交拋物線于P、Q兩點,若線
段PF與FQ的長分別是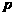 、
、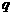 ,則
,則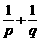 等于
等于
(A)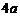 (B)
(B) (C)
(C)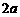 (D)
(D)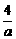
(12)如圖,OA是圓錐底面中心O到母線的垂線,OA繞軸旋轉一周所得曲
面將圓錐分成體積相等的兩部分,則母線與軸的夾角的余弦值為
 (A)
(A)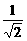 (B)
(B)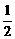
(C)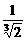 (D)
(D)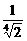
第II卷(非選擇題 90分)
22.[解](1)由題設,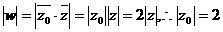 ,
,
于是由 ,
…(3分)
,
…(3分)
因此由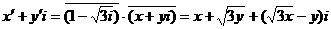 ,
,
得關系式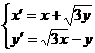 …(5分)
…(5分)
[解](2)設點 在直線
在直線 上,則其經(jīng)變換后的點
上,則其經(jīng)變換后的點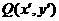 滿足
滿足
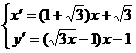 ,
…(7分)
,
…(7分)
消去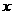 ,得
,得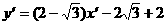 ,
,
故點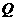 的軌跡方程為
的軌跡方程為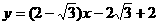 …(10分)
…(10分)
[解](3)假設存在這樣的直線,∵平行坐標軸的直線顯然不滿足條件,
∴所求直線可設為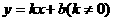 ,
…(12分)
,
…(12分)
[解法一]∵該直線上的任一點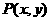 ,其經(jīng)變換后得到的點
,其經(jīng)變換后得到的點
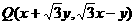 仍在該直線上,
仍在該直線上,
∴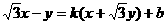 ,
,
即 ,
,
當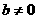 時,方程組
時,方程組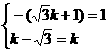 無解,
無解,
故這樣的直線不存在。 …(16分)
當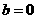 時,由
時,由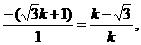
得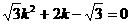 ,
,
解得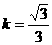 或
或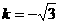 ,
,
故這樣的直線存在,其方程為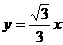 或
或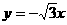 ,
…(18分)
,
…(18分)
[解法二]取直線上一點 ,其經(jīng)變換后的點
,其經(jīng)變換后的點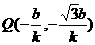 仍在該直線上,
仍在該直線上,
∴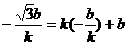 ,
,
得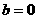 ,
…(14分)
,
…(14分)
故所求直線為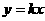 ,取直線上一點
,取直線上一點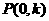 ,其經(jīng)變換后得到的點
,其經(jīng)變換后得到的點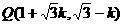 仍在該直線上。
仍在該直線上。
∴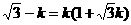 ,
…(16分)
,
…(16分)
即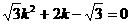 ,得
,得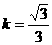 或
或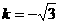 ,
,
故這樣的直線存在,其方程為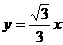 或
或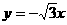 ,
…(18分)
,
…(18分)
21.[解](1)由題意,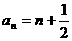 ,∴
,∴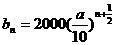 ,
…(4分)
,
…(4分)
[解](2)∵函數(shù)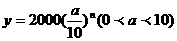 遞減,
遞減,
∴對每個自然數(shù)n,有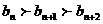 ,則以
,則以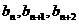 為邊長能構成一個三角形的充要條件是
為邊長能構成一個三角形的充要條件是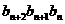 ,
,
即 …(7分)
…(7分)
解得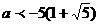 或
或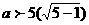 ∴
∴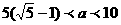 ,
…(10分)
,
…(10分)
[解](3)∴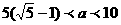 ∴
∴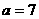
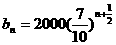 …(12分)
…(12分)
數(shù)列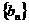 是一個遞減的正數(shù)數(shù)列,對每個自然數(shù)
是一個遞減的正數(shù)數(shù)列,對每個自然數(shù)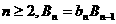 ,
,
于是當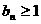 時,
時,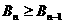 ,當
,當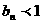 時,
時,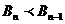 ,
,
因此,數(shù)列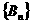 的最大項的項數(shù)
的最大項的項數(shù)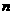 滿足不等式
滿足不等式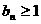 且
且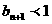 。
。
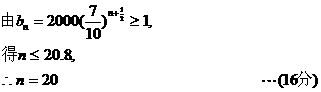
20. [解](1)
[解](1)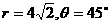 ,得指令為
,得指令為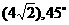 , …(4分)
, …(4分)
(2)設機器人最快在點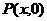 處截住小球 …(6分)
處截住小球 …(6分)
則因為小球速度是機器人速度的2倍,所以在相同時間內(nèi)有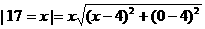 ,…(8分)。
,…(8分)。
即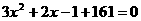 ,得
,得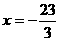 或
或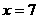 ,
,
∵要求機器人最快地去截住小球,即小球滾動距離最短,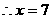 ,
,
故機器人最快可在點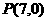 處截住小球,
(10分)
處截住小球,
(10分)
所給的指令為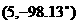 ,
(14分)
,
(14分)
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com