
題目列表(包括答案和解析)
3、使得點A(cos2α,sin2α)到點B(cosα,sinα)的距離為1的α 的一個值是( )
A.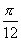 B.
B.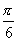
C.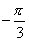 D.
D.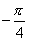
2、在等比數列{an}中,an>0 ,且a2=1-a1 ,a4=9-a3 ,則a4+a5 =( )
A.16 B.27
C.36 D.81
1、已知向量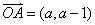 的模為
的模為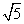 ,則實數a的值是( )
,則實數a的值是( )
A.-1 B.2
C.-1 或2 D.1或-2
22、解:
(1)圓F1的方程是(x+c)2+y2=(a-c)2,
因為B2M、B2N與該圓切于M、N點,所以B2、M、F1、N四點共圓,
且B2F1為直徑,則過此四點的圓的方程是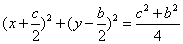 ,
,
從而兩個圓的公共弦MN的方程為
cx+by+c2=(a-c)2,又點B1在MN上,∴a2+b2-2ac=0;∵b2=a2-c2,
∴2a2-2ac-c2=0,即e2+2e-2=0,∴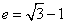 (負值舍去);
(負值舍去);
(2)由(1),MN的方程為cx+by+c2=(a-c)2,由已知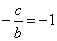 ,∴b=c,
,∴b=c,
而原點到MN的距離
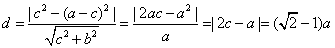 ,
,
∴a=4,b2=c2=8,所求橢圓方程是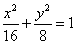 ;
;
(3)假設這樣的橢圓存在,由(2)則有
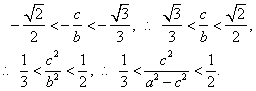 .
.
故得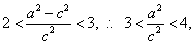 求得
求得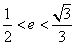 ,
,
即當離心率取值范圍是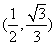 時,
時,
直線MN的斜率可以在區間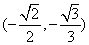 內取值.
內取值.
21、解:
(1)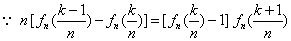 ,
,
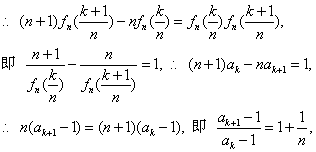
由n為定值,則數列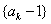 是以
是以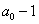 為首項,
為首項,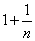 為公比的等比數列,
為公比的等比數列,
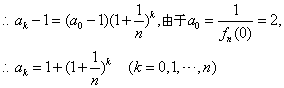
(2)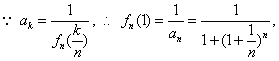

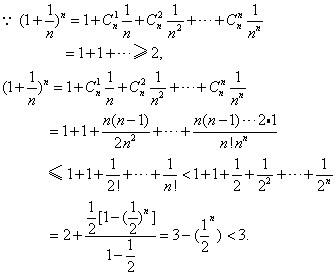
20、解:
(1)由概率分布的性質2有,0.12+0.18+0.20+0.20+100a2+3a+4a=1,
∴100a2+7a=0.3,∴ 1000a2+70a-3=0,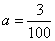 ,
,
或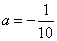 (舍去),即a=0.03,
(舍去),即a=0.03,
∴100a2+3a=0.18,4a=0.12,∴ξ的分布列為
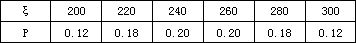
∴Eξ=200×0.12+220×0.18+240×0.20+260×0.20+280×0.18+300×0.12=250(km)
Dξ=502×0.12+302×0.18+102×0.20+102×0.20+302×0.18+502×0.12=964;
(2)由已知η=3ξ-3(ξ>3,ξ∈Z),∴ Eη=E(3ξ-3)=3Eξ-3=3×250-3=747(元),
Dη=D(3ξ-3)=32Dξ=8676.
19、解:
建立空間直角坐標系,使得D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),M(0,0,a),E(a,0,a),F(0,a,a),則由中點坐標公式得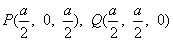 ,
,
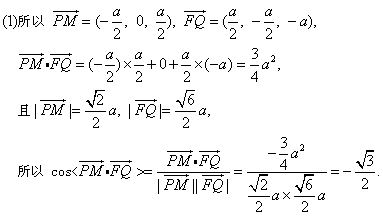
故得兩向量所成的角為150°;
(2)設n=(x,y,z)是平面EFB的單位法向量,即|n|=1,n⊥平面EFB,
所以n⊥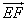 ,且n⊥
,且n⊥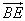 ,又
,又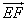 =(-a,a,0),
=(-a,a,0),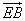 =(0,a, -a).
=(0,a, -a).
即有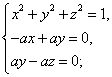 得其中的一個解是
得其中的一個解是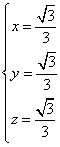 ,
,
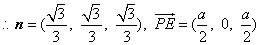 .
.
設所求距離為d,則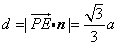 .
.
(3)設e=(x1,y1,z1)是兩異面直線的公垂線上的單位方向向量,
則由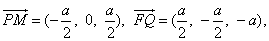 得
得
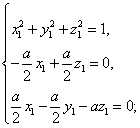 求得其中的一個
求得其中的一個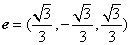 ,
,
而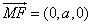 ,設所求距離為m,則
,設所求距離為m,則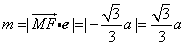
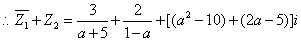 的虛部為0,
的虛部為0,
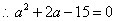 ,解得a=-5,或a=3,又分母不為零,∴a=3,
,解得a=-5,或a=3,又分母不為零,∴a=3,
此時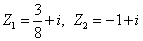 ,即
,即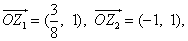
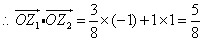 .
.
18、解:
(1)∵a∈{a|20<12a-a2},∴a2-12a+20<0,即2<a<10,∴函數y=logax是增函數;
(2) ,
,
必有x>0,當0<x<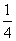 時,
時,
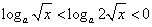 ,
,
不等式化為 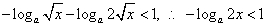 ,
,
故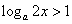 ,
,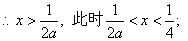
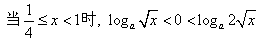 ,
,
不等式化為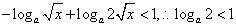 ,
,
這顯然成立,此時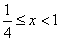 ;
;
當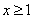 時,
時,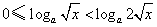 ,不等式化為
,不等式化為
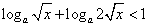 ,
,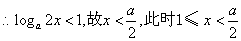 ;
;
綜上所述知,使命題p為真命題的x的取值范圍是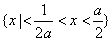 .
.
16、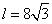 提示:由4a+2=2a-2,得a=-2,∴平移后拋物線的焦點為F(-4,-6),
提示:由4a+2=2a-2,得a=-2,∴平移后拋物線的焦點為F(-4,-6),
又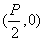 在y=x-2上,∴p=4,由此可求得平移公式為
在y=x-2上,∴p=4,由此可求得平移公式為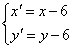 ,
,
代入原方程得平移后的拋物線方程是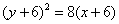 ,
,
令x=0,得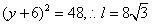
15、 提示:由面積公式
提示:由面積公式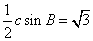 得c=4,由余弦定理得
得c=4,由余弦定理得
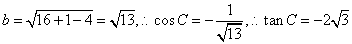 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com