
題目列表(包括答案和解析)
1. 已知二次函數f(x)=(x-a)(x-b)-2(a<b),并且α、β(α<β)是方程f(x)=0的兩根,則a、b、α、β的大小關系是
A.α<a<b<β B.a<α<β<b
C.a<α<b<β D.α<a<β<b
 (13)用平面
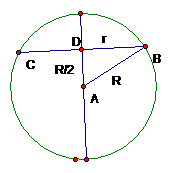
(13)用平面 截半徑為R的球,如果球心到平面
截半徑為R的球,如果球心到平面 的距離為
的距離為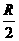 ,那么截得小圓的面積與球的表面積的比值為______________.
,那么截得小圓的面積與球的表面積的比值為______________.
講解:設截得小圓的半徑是 ,球的半徑是R, 畫一個軸截面圖形. 在
,球的半徑是R, 畫一個軸截面圖形. 在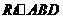 中,顯然,
中,顯然,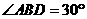 ,于是
,于是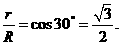
故截得小圓的面積與球的表面積的比值為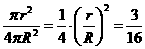 ,應填
,應填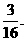
評注:題中的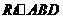 就是我們常用的三角板模型,它是高考的熱門話題.
就是我們常用的三角板模型,它是高考的熱門話題.
(14)函數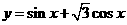 在區間
在區間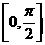 上的最小值為_____________.
上的最小值為_____________.
講解:將函數式變形為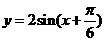 . 由
. 由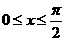 ,得
,得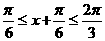 . 于是,函數的最小值為
. 于是,函數的最小值為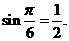 應填
應填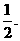
評注:如果畫出函數的圖象,就可看出最小值對應的點是函數圖象的左端點.
(15)已知函數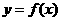 是奇函數,當
是奇函數,當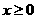 時,
時,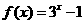 . 設
. 設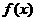 的反函數是
的反函數是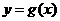 ,則
,則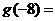 ________.
________.
講解:易求得:當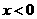 時,
時, . 這樣由
. 這樣由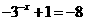 ,解得
,解得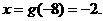 應填
應填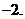
評注:反函數的定義域是原函數的值域.
(16)設P是曲線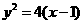 上的一個動點,則點P到點
上的一個動點,則點P到點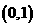 的距離與點P到
的距離與點P到 軸的距離之和的最小值是______________.
軸的距離之和的最小值是______________.
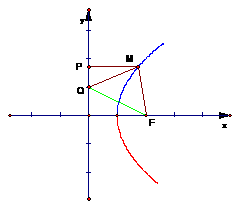 講解:顯然,
講解:顯然, 軸是拋物線
軸是拋物線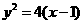 的準線,而
的準線,而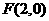 是拋物線的焦點,于是
是拋物線的焦點,于是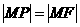 .
.
如圖,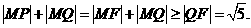
應填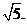
評注:如果聯想到拋物線的定義,就容易找到解題的開竅點.
(1)設集合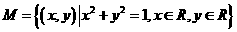 ,
,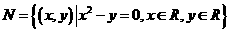 ,則集合
,則集合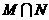 中元素的個數為( )
中元素的個數為( )
A.1 B. 2 C. 3 D. 4
講解:在同一坐標系中,作出單位圓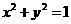 和拋物線
和拋物線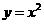 的圖形,易知它們有兩個交點,應選B.
的圖形,易知它們有兩個交點,應選B.
評注:也可通過解如下方程組求解:
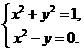
(2)函數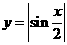 的最小正周期是( )
的最小正周期是( )
A. 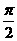 B.
B. 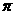 C.
C.
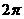 D.
D.
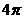
講解:作出函數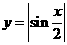 的圖象,易知最小正周期是
的圖象,易知最小正周期是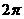 ,應選C.
,應選C.
評注:函數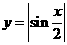 的最小正周期是函數
的最小正周期是函數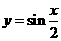 的一半.
的一半.
(3) 設數列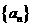 是等差數列,且
是等差數列,且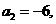
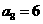 ,
,  是數列
是數列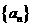 的前
的前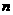 項的和,則( )
項的和,則( )
A.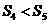 B.
B.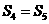 C.
C.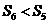 D.
D.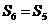
講解:由題意得 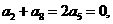 即
即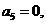 于是
于是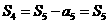 ,應選B.
,應選B.
評注:一般解法是:設等差數列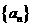 的公差是
的公差是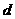 ,則有已知,得
,則有已知,得
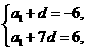 解出
解出 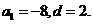 于是
于是 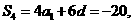
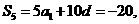
從而 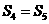 ,應選B.
,應選B.
(4) 圓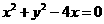 在點
在點 處的切線方程是( )
處的切線方程是( )
A. 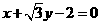 B.
B.
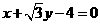
C. 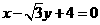 D.
D.
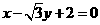
講解:顯然,點 的坐標不適合方程A, C,從而應否定A, C; 將圓的方程化為
的坐標不適合方程A, C,從而應否定A, C; 將圓的方程化為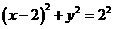 ,圓心
,圓心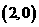 到直線
到直線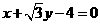 的距離為
的距離為
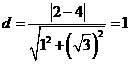 ,不是圓的半徑2,故應選D.
,不是圓的半徑2,故應選D.
評注:一般解法為:設圓的切線方程是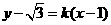 ,即
,即 ,
,
則圓心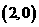 到切線
到切線 的距離為
的距離為
 解出
解出 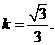
(5) 函數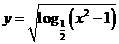 的定義域是( )
的定義域是( )
A. 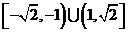 B.
B.
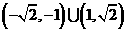
C. 
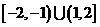 D.
D.
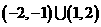
講解: 取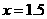 ,有
,有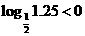 ,否定C, D; 取
,否定C, D; 取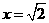 ,有
,有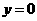 ,否定B. 應選A.
,否定B. 應選A.
評注:一般解法為:由題意得 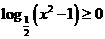 ,即
,即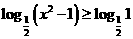 , 等價于
, 等價于 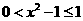 .
.
(6) 設復數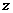 的幅角的主值為
的幅角的主值為 ,虛部為
,虛部為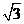 ,則
,則 ( )
( )
A. 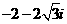 B.
B.
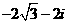
C. 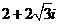 D.
D.
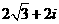
講解:設復數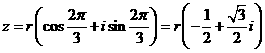 , 則有
, 則有 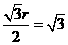 ,
,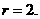 于是
于是 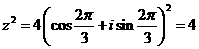
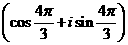 =
=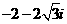 .應選A.
.應選A.
評注:也可用代數形式: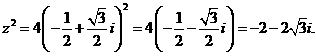
(7) 設雙曲線的焦點在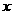 軸上,兩條漸近線為
軸上,兩條漸近線為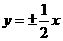 ,則雙曲線的離心率
,則雙曲線的離心率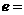 ( )
( )
A. 5 B. 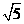 C.
C. 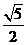 D.
D.
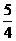
講解:設雙曲線的方程是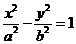 ,其兩條漸近線為
,其兩條漸近線為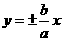 ,于是
,于是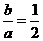 ,即有
,即有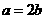 ,有
,有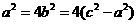 ,
,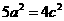 ,即
,即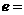
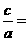
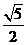 .應選C.
.應選C.
評注:雙曲線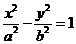 對于的兩條漸近線為
對于的兩條漸近線為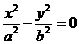 ,也就是
,也就是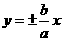 .
.
(8) 不等式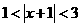 的解集為( )
的解集為( )
A. 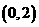 B.
B.
 C.
C. 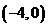 D.
D. 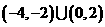
講解:取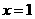 ,適合不等式,否定C; 取
,適合不等式,否定C; 取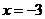 ,適合不等式,否定A, B. 應選D.
,適合不等式,否定A, B. 應選D.
評注:一種直接解法是:由原不等式得
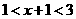 或
或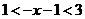 ,即
,即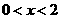 或
或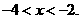
(9) 正三棱錐的底面邊長為2,側面均為直角三角形,則此三棱柱的體積為( )
A. 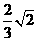 B.
B. 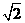 C.
C. 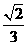 D.
D. 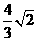
講解:顯然,側面是等腰直角三角形,其直角邊為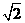 ,于是三棱柱的體積為
,于是三棱柱的體積為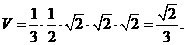 應選C.
應選C.
評注:本題的模型是正方體截下的一個,教室的一個墻角. 當中的體積計算需要轉換角度思考問題.
(10) 在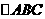 中,
中,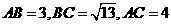 ,則邊
,則邊 上的高為( )
上的高為( )
A. 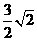 B.
B.
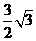 C.
C.
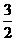 D.
D.
講解:由余弦定理 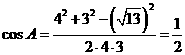 ,得
,得
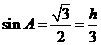 ,有
,有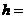
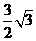 .應選B.
.應選B.
評注:請讀者自己補上幾何圖形.
(11) 設函數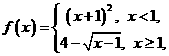 則使得
則使得 的自變量
的自變量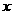 的取值范圍為( )
的取值范圍為( )
A.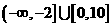 B.
B. 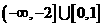
C. 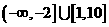 D.
D.
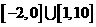
講解:取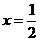 ,有
,有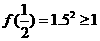 成立,否定C, D;取
成立,否定C, D;取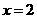 ,
,
有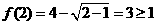 成立,否定B. 應選A.
成立,否定B. 應選A.
評注:分段函數常考常新. 本題也可給出直接解法,圖象解法.
(12) 將4名教師分配到3所中學任教,每所中學至少1名教師,則不同的分配方案共有( )
A. 12 種 B. 24 種 C 36 種 D. 48 種
講解: 本題可以給出一種直接解法 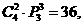 應選C.
應選C.
評注: 請讀者用文字語言表述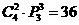 的實際意義. 再想想:解法
的實際意義. 再想想:解法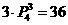 是否正確?
是否正確?
22、(14分)已知數列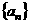 的前
的前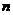 項和
項和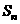 滿足
滿足
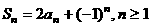
(1)
寫出數列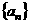 的前三項
的前三項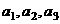 ;
;
(2)
求數列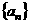 的通項公式;
的通項公式;
(3)
證明:對任意的整數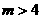 ,有
,有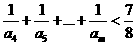 .
.
18、(12分)解方程 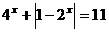
19(12分)某村計劃建造一個室內面積為800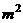 的矩形蔬菜溫室。在溫室內,沿左、右兩端與后側內墻各保留1
的矩形蔬菜溫室。在溫室內,沿左、右兩端與后側內墻各保留1 寬的通道,沿前側內墻保留3
寬的通道,沿前側內墻保留3 寬的空地。當矩形溫室的邊長各為多少時?蔬菜的種植面積最大。最大種植面積是多少?
寬的空地。當矩形溫室的邊長各為多少時?蔬菜的種植面積最大。最大種植面積是多少?
20(12分)三棱錐P-ABC中,側面PAC與底面ABC垂直,PA=PB=PC=3,
(1) 求證:AB ⊥ BC;
(2)





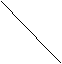 設AB=BC=
設AB=BC=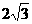 ,求AC與平面PBC所成角的大小.
,求AC與平面PBC所成角的大小.
21(12分)設橢圓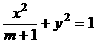 的兩個焦點是
的兩個焦點是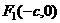 與
與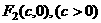 ,且橢圓上存在一點
,且橢圓上存在一點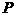 ,使得直線
,使得直線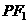 與
與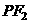 垂直.
垂直.
(1)求實數 的取值范圍;
的取值范圍;
(2)設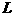 是相應于焦點
是相應于焦點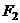 的準線,直線
的準線,直線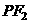 與
與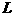 相交于點
相交于點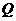 ,若
,若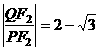 ,求直線
,求直線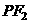 的方程.
的方程.
17、(12分)已知 為銳角,且
為銳角,且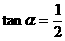 ,求
,求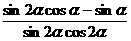 的值。
的值。
16、設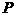 是曲線
是曲線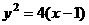 上的一個動點,則點
上的一個動點,則點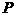 到點
到點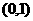 的距離與點
的距離與點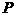 到
到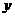 軸的距離之和的最小值為
.
軸的距離之和的最小值為
.
15、已知函數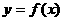 是奇函數,當
是奇函數,當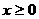 時,
時,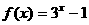 ,設
,設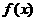 的反函數是
的反函數是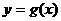 ,則
,則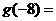 .
.
14、函數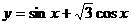 在區間
在區間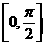 上的最小值為
.
上的最小值為
.
13、用平面 截半徑為
截半徑為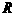 的球,如果球心到平面
的球,如果球心到平面 的距離為
的距離為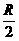 ,那么截得小圓的面積與球的表面積的比值為
.
,那么截得小圓的面積與球的表面積的比值為
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com