
題目列表(包括答案和解析)
4. 已知一個簡單多面體的每一個面都是三角形,以每一個頂點為一端都有5條棱,則此多面體的棱數為 A.30 B.32 C.20 D.18
3. 下列各組向量中,共線的是 A.=(-2,3),=(4,6) B.=(2,3),=(3,2) C.=(1,-2),=(7,14) D.=(-3,2),=(6,-4)
2. 設P、Q是兩個非空集合,定義P*Q={(a,b)|a∈P,b∈Q},若P={0,1,2},Q={1,2,3,4},則P*Q中元素的個數是 A.4個 B.7個 C.12個 D.16個
1. 已知雙曲線的離心率為,則它的兩條漸近線的夾角為 A.30º B.45º C.60º D.90º
(17)(本小題滿分10分)
已知 ,
, ,
, },求
},求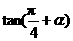 的值.
的值.
(18)(本小題滿分10分)
已知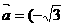 ,
, ),
), ,
, ),求
),求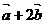 與
與 的夾角
的夾角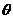 的值.
的值.
(19)(本小題滿分12分)
已知等比數列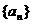 中,
中,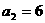 ,
,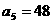 ,求
,求 及前6項和
及前6項和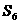 .
.
(20)(本小題滿分14分)
如圖綜7,三棱柱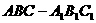 中,
中,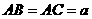 ,
,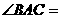 90°,頂點
90°,頂點 在底面ABC上的射影為BC邊的中點M.
在底面ABC上的射影為BC邊的中點M.
(Ⅰ)求證:BC垂直于過三點A1、A、M的平面;
(Ⅱ)如果平面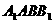 與平面ABC所成的二面角為60°,求三棱柱
與平面ABC所成的二面角為60°,求三棱柱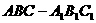 的體積.
的體積.
(21)(本小題滿分14分)
設函數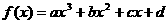 的圖象與y軸的交點為P,且曲線在P點處的切線方程為
的圖象與y軸的交點為P,且曲線在P點處的切線方程為 .若函數
.若函數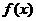 在x=2處取得極小值-16.
在x=2處取得極小值-16.
(Ⅰ)求函數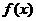 的解析式;
的解析式;
(Ⅱ)確定函數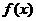 的單調減小區間.
的單調減小區間.
(22)(本小題滿分14分)
已知雙曲線 的離心率
的離心率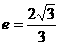 ,過點A(0,-b)和B(a,0)的直線與原點間的距離為
,過點A(0,-b)和B(a,0)的直線與原點間的距離為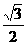 .
.
(Ⅰ)確定這個雙曲線的方程;
(Ⅱ)直線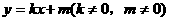 與雙曲線交于兩個不同的點C、D,并且C、D兩點都在以A為圓心的同一個圓上,求實數m的取值范圍.
與雙曲線交于兩個不同的點C、D,并且C、D兩點都在以A為圓心的同一個圓上,求實數m的取值范圍.
(13)直線 與兩坐標軸所構成的三角形的面積為
與兩坐標軸所構成的三角形的面積為 ,則
,則 =________.
=________.
(14) =________.
=________.
(15)如果復數 ,那么z的三角形式是________.
,那么z的三角形式是________.
(16)正方體的對角線長為l,那么它的體積為________.
(1)已知全集U=R,集合 ,
,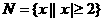 ,則(
,則(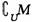 )∪(
)∪( )=( ).
)=( ).
A. B.
B.
C.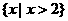 D.
D.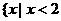 或
或
(2)函數 是( ).O
是( ).O
A.周期為π的偶函數 B.周期為π的奇函數
C.周期為1的偶函數 D.周期為1的奇函數
(3)已知空間四邊形的四邊長都相等,那么順次連結各邊中點的四邊形一定是( ).
A.梯形 B.菱形 C.矩形 D.正方形
(4)函數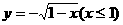 的反函數是( ).
的反函數是( ).
A. B.
B.
C.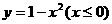 D.
D.
(5)拋物線 的準線方程是( ).
的準線方程是( ).
A.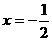 B.
B.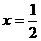 C.
C. D.
D.
(6)已知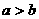 ,
, ,則下列不等式中一定成立的是( ).
,則下列不等式中一定成立的是( ).
A.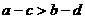 B.
B.
C.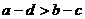 D.
D.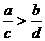
(7)若向量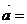 (1,1),
(1,1), (1,-1),
(1,-1), (-1,2),則
(-1,2),則 ( ).
( ).
A. B.
B.
C. D.
D.
(8) 的展開式中,常數項是( ).
的展開式中,常數項是( ).
A.第4項 B.第5項 C.第6項 D.第7項
(9)從數字1,2,3,4,5中任取兩個不同的數字構成一個兩位數,則這個兩位數大于40的概率是( ).
A. B.
B.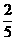 C.
C. D.
D.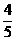
(10)曲線 在點
在點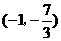 處的切線的傾斜角是( ).
處的切線的傾斜角是( ).
A.45° B.135° C.30° D.150°
(11)等差數列 中,若
中,若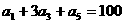 ,則
,則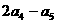 =( ).
=( ).
A.-8 B.20 C.22 D.24
(12)在正三棱錐 中,M、N分別是側棱PB、PC的中點,若截面
中,M、N分別是側棱PB、PC的中點,若截面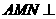 側面PBC,則此三棱錐的側棱與底面所成角的正切值是( ).
側面PBC,則此三棱錐的側棱與底面所成角的正切值是( ).
A.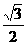 B.
B.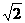 C.
C.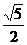 D.
D.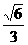
(17)(本小題滿分12分)
制造某種零件,甲機床的廢品率為0.04,乙機床的廢品率為0.05,從這二機床生產的產品中各抽出一件作檢驗,求
(Ⅰ)其中恰有一件廢品的概率;
(Ⅱ)其中至多有一件廢品的概率;
(Ⅲ)其中沒有廢品的概率.
(18)(本小題滿分12分)
數列 的前n項的和為
的前n項的和為 ,且
,且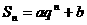 .其中
.其中 ,
,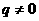 ,
, .
.
(Ⅰ)若數列 是公比為q的等比數列,求證
是公比為q的等比數列,求證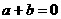 ;
;
(Ⅱ)若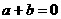 ,求證數列
,求證數列 是等比數列.
是等比數列.
(19)(本小題滿分12分)
正方體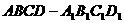 中,E、F分別為AB、BB1的中點(如圖綜10).
中,E、F分別為AB、BB1的中點(如圖綜10).
(Ⅰ)證明EF∥平面 ;
;
(Ⅱ)求二面角 的平面角的正切值;
的平面角的正切值;
(Ⅲ)若 ,求三棱錐
,求三棱錐 的體積.
的體積.

綜10
(20)(本小題滿分12分)
已知函數 .
.
(Ⅰ)求此函數的定義域及單調遞增區間;
(Ⅱ)求此函數的極大值和極小值.
(21)(本小題滿分12分)
已知甲、乙、丙三種食品的維生素A、B的含量及成本如下表:
|
|
甲 |
乙 |
丙 |
|
維生素A含量(單位/千克) |
600 |
700 |
400 |
|
維生素B含量(單位/千克) |
800 |
400 |
500 |
|
成本(元/千克) |
11 |
9 |
4 |
某食品研究所想用x千克甲種食品、y千克乙種食品、z千克丙種食品配制成100千克的混合食品,并使混合食品中至少含有56000單位的維生素A、63000單位的維生素B.
(Ⅰ)用x、y表示這種混合食品的總成本C(元);
(Ⅱ)確定x、y、z的值,使混合食品的總成本最低.
(22)(本小題滿分14分)
已知雙曲線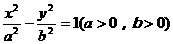 的左、右兩個頂點分別為A、B,過這雙曲線右焦點F2且與x軸垂直的直線交雙曲線于兩點P、Q、P在x軸上方,且
的左、右兩個頂點分別為A、B,過這雙曲線右焦點F2且與x軸垂直的直線交雙曲線于兩點P、Q、P在x軸上方,且 ,
,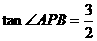 .
.
(Ⅰ)求這雙曲線的方程;
(Ⅱ)若直線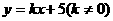 與雙曲線交于不同兩點M、N,且M、N都在以E(0,-1)為圓心的同一個圓上,求k的值.
與雙曲線交于不同兩點M、N,且M、N都在以E(0,-1)為圓心的同一個圓上,求k的值.
(13)若雙曲線 的一個焦點到一條漸近線的距離為
的一個焦點到一條漸近線的距離為 ,則a=________.
,則a=________.
(14)若 ,則a=________.
,則a=________.
(15)把正方形ABCD沿對角線BD折成直二面角后,得到的三棱錐A-BCD中,有以下四個結論:
① ;
②△
;
②△ 是等邊三角形;
是等邊三角形;
③AB與面BCD成60°角; ④AB和CD成60°角.
那么以上結論中,正確結論的序號是________.
(16)(理科)一個袋子里有大小相同的3個紅球和2個白球,從中同時取出2個,則其中含紅球個數的數學期望是________.(用數字作答)
(文科)一個工廠有若干個車間,今采用分層抽樣方法從全廠某天的2048件產品中抽取一個容量為128的樣本進行質量檢查.若一車間這一天生產256件產品,則從該車間抽取的產品件數為________.
(1)a=3是直線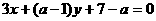 和
和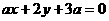 平行且不重合的( ).
平行且不重合的( ).
A.充分非必要條件 B.必要非充分條件
C.充要條件 D.既非充分條件也非必要條件
(2)在等差數列 中,
中,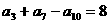 ,
, ,那么其前13項的和
,那么其前13項的和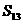 等于( ).
等于( ).
A.168 B.156 C.78 D.152
(3)已知定點M和定直線l,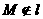 ,那么經過點M且與直線l相切的動圓的圓心的軌跡是( ).
,那么經過點M且與直線l相切的動圓的圓心的軌跡是( ).
A.直線 B.二條平行直線
C.圓 D.拋物線
(4)已知函數: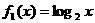 ,
,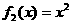 ,
,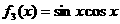 ,
,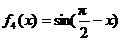 .從中任取兩個相乘得到若干個函數,所得這些函數中偶函數共有( ).
.從中任取兩個相乘得到若干個函數,所得這些函數中偶函數共有( ).
A.1個 B.2個 C.3個 D.4個
(5)已知向量 、
、 的夾角為90°,且
的夾角為90°,且 ,記
,記 ,
, ,若
,若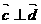 ,則k=( ).
,則k=( ).
A.-6 B.6 C.3 D.-3
(6)若點P在直線 上移動,PA、PB是圓
上移動,PA、PB是圓 的兩條切線,A、B是切點,O是原點,則四邊形PAOB的面積最小值為( ).
的兩條切線,A、B是切點,O是原點,則四邊形PAOB的面積最小值為( ).
A.24 B.16 C.8 D.4
(7)點P在曲線 上移動時,過點P曲線的切線的傾斜角的取值范圍是( ).
上移動時,過點P曲線的切線的傾斜角的取值范圍是( ).
A. ,
, ]
B.[
]
B.[ ,p ]
,p ]
C. ,
,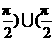 ,
, D.
D. ,
, ,p )
,p )
(8)從6名志愿者中選出4人分別從事翻譯、導游、導購、保潔四項不同的工作,若其中甲、乙兩名志愿者都不能從事翻譯工作,則選派方案共有( ).
A.280種 B.240種 C.180種 D.96種
(9)已知圓錐軸截面是邊長為2的等邊三角形,當它的內接圓柱的側面積最大時,內接圓柱的高為( ).
A.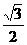 B.
B.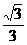 C.
C. D.
D.
(10)已知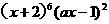 的展開式中,
的展開式中, 項的系數為100,那么實數a的值為( ).
項的系數為100,那么實數a的值為( ).
A.0或 B.
B. 或
或 C.0或
C.0或 D.
D. ,-
,-
(11)設 是由正數組成的等差數列,
是由正數組成的等差數列, 是由正數組成的等比數列,且
是由正數組成的等比數列,且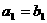 .若存在自然數m,使得
.若存在自然數m,使得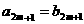 ,則必有( ).
A.
,則必有( ).
A. B.
B.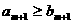
C. D.
D.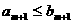
(12)二次函數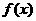 的二次項系數為正數,且對任意
的二次項系數為正數,且對任意 R都有
R都有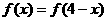 成立,若
成立,若 ,則x的取值范圍是( ).
,則x的取值范圍是( ).
A. B.
B. 或
或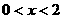
C.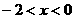 D.
D. 或
或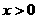
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com