
題目列表(包括答案和解析)
(17)設函數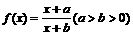 ,求
,求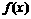 的單調區間,并證明
的單調區間,并證明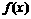 在其單調區間上的單調性.
在其單調區間上的單調性.
(18)已知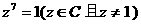 .
.
(Ⅰ)證明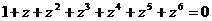 ;
;
(Ⅱ)設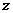 的輻角為
的輻角為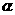 ,求
,求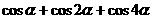 的值.
的值.
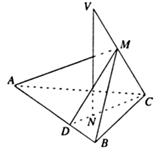
(19)已知VC是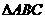 所在平面的一條斜線,點N是V在平面ABC上的射影,且在
所在平面的一條斜線,點N是V在平面ABC上的射影,且在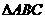 的高CD上.
的高CD上.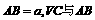 之間的距離為
之間的距離為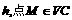 .
.
(Ⅰ)證明∠MDC是二面角M–AB–C的平面角;
(Ⅱ)當∠MDC=∠CVN時,證明VC ;
;
(Ⅲ)若∠MDC=∠CVN=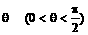 ,求四面體MABC的體積.
,求四面體MABC的體積.
(20)在1與2之間插入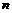 個正數
個正數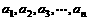 ,使這
,使這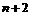 個數成等比數列;又在1與2之間插入
個數成等比數列;又在1與2之間插入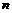 個正數
個正數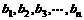 ,使這
,使這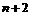 個數成等差數列.記
個數成等差數列.記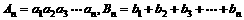 .
.
(Ⅰ)求數列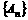 和
和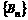 的通項;
的通項;
(Ⅱ)當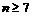 時,比較
時,比較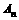 與
與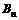 的大小,并證明你的結論.
的大小,并證明你的結論.
(21)某摩托車生產企業,上年度生產摩托車的投入成本為1萬元/輛,出廠價為1.2萬元/輛,年銷售量為1000輛.本年度為適應市場需求,計劃提高產品檔次,適度增加投入成本.若每輛車投入成本增加的比例為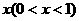 ,則出廠價相應提高的比例為0.75
,則出廠價相應提高的比例為0.75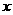 ,同時預計年銷售量增加的比例為0.6
,同時預計年銷售量增加的比例為0.6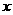 .已知年利潤=(出廠價–投入成本)
.已知年利潤=(出廠價–投入成本)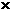 年銷售量.
年銷售量.
(Ⅰ)寫出本年度預計的年利潤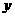 與投入成本增加的比例
與投入成本增加的比例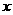 的關系式;
的關系式;
(Ⅱ)為使本年度的年利潤比上年有所增加,問投入成本增加的比例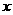 應在什么范圍內?
應在什么范圍內?
(22)已知拋物線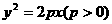 .過動點M(
.過動點M(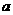 ,0)且斜率為1的直線
,0)且斜率為1的直線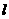 與該拋物線交于不同的兩點A、B,
與該拋物線交于不同的兩點A、B,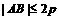 .
.
(Ⅰ)求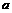 的取值范圍;
的取值范圍;
(Ⅱ)若線段AB的垂直平分線交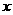 軸于點N,求
軸于點N,求 面積的最大值.
面積的最大值.
普通高等學校春季招生考試
數學試題(理工農醫類)參考解答及評分標準
說明:
(13)已知球內接正方體的表面積為S,那么球體積等于_______________.
(14)橢圓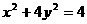 長軸上一個頂點為A,以A為直角頂點作一個內接于橢圓的等腰直角三角形,該三角形的面積是_______________.
長軸上一個頂點為A,以A為直角頂點作一個內接于橢圓的等腰直角三角形,該三角形的面積是_______________.
(15)已知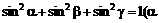 、
、 、
、 均為銳角),那么
均為銳角),那么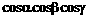 的最大值等于____________________.
的最大值等于____________________.
(16)已知 、
、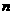 是直線,
是直線,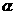 、
、 、
、 是平面,給出下列命題:
是平面,給出下列命題:
① 若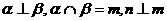 ,則
,則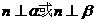 ;
;
②若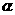 ∥
∥ ,
, ,則
,則 ∥
∥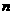 ;
;
③若 不垂直于
不垂直于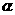 ,則
,則 不可能垂直于
不可能垂直于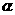 內的無數條直線;
內的無數條直線;
④若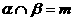 ,
,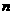 ∥
∥ ,且
,且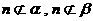 ,則
,則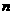 ∥
∥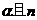 ∥
∥ .
.
其中正確的命題的序號是_______________(注:把你認為正確的命題的序號都填上)
(1)集體 的子集個數是
的子集個數是
(A)32 (B)31 (C)16 (D)15
(2)函數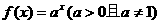 對于任意的實數
對于任意的實數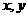 都有
都有
(A)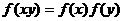 (B)
(B)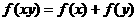
(C)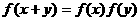 (D)
(D)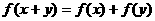
(3)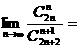
(A)0 (B)2 (C) (D)
(D)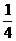
(4)函數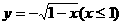 的反函數是
的反函數是
(A)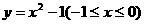 (B)
(B)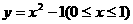
(C) (D)
(D)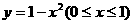
(5)極坐標系中,圓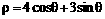 的圓心的坐標是
的圓心的坐標是
(A) (B)
(B) (C)
(C) (D)
(D)
(6)設動點P在直線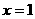 上,O為坐標原點.以OP為直角邊、點O為直角頂點作等腰
上,O為坐標原點.以OP為直角邊、點O為直角頂點作等腰 ,則動點Q的軌跡是
,則動點Q的軌跡是
(A)圓 (B)兩條平行直線 (C)拋物線 (D)雙曲線
(7)已知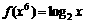 ,那么
,那么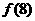 等于
等于
(A)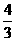 (B)8 (C)18 (D)
(B)8 (C)18 (D)
(8)若A、B是銳角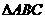 的兩個內角,則點
的兩個內角,則點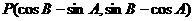 在
在
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(9)如果圓錐的側面展開圖是半圓,那么這個圓錐的頂角(圓錐軸截面中兩條母線的夾角)是
(A)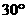 (B)
(B)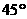 (C)
(C) (D)
(D)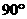
(10)若實數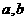 滿足
滿足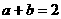 ,則
,則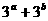 的最小值是
的最小值是
(A)18 (B)6 (C)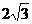 (D)
(D)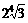
(11)右圖是正方體的平面展開圖.在這個正方體中,
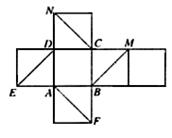 ①
①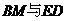 平行
平行
②CN與BE是異面直線
③CN與BM成 角
角
④DM與BN垂直
以上四個命題中,正確命題的序號是
(A)①②③ (B)②④
(C)③④ (D)②③④
(12)根據市場調查結果,預測某種家用商品從年初開始的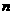 個月內累積的需求量
個月內累積的需求量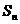 (萬件)近似地滿足
(萬件)近似地滿足
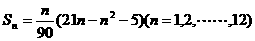
按此預測,在本年度內,需求量超過1.5萬件的月份是
(A)5月、6月 (B)6月、7月 (C)7月、8月 (D)8月、9月
第Ⅱ卷(非選擇題共90分)
|
已知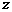 是復數,
是復數,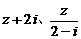 均為實數(
均為實數(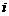 為虛數單位),且復數
為虛數單位),且復數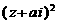 在復平面上對應的點在第一象限,求實數
在復平面上對應的點在第一象限,求實數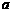 的取值范圍.
的取值范圍.
[解]
|
已知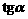 是方程
是方程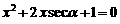 的兩個根中較小的根,求
的兩個根中較小的根,求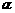 的值.
的值.
[解]
|
第2小題滿分8分.
已知正三棱錐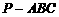 的體積為
的體積為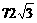 ,側面與底面所成的二面角的大小為
,側面與底面所成的二面角的大小為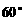 .
.
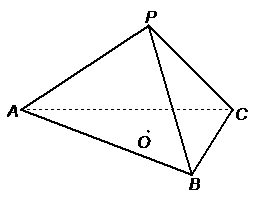 (1)證明:
(1)證明: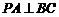 ;
;
(2)求底面中心 到側面的距離.
到側面的距離.
[證明](1)
[解](2)
|
第2小題滿分8分.
某市2004年底有住房面積1200萬平方米,計劃從2005年起,每年拆除20萬平方米的舊住房. 假定該市每年新建住房面積是上年年底住房面積的5%.
(1)分別求2005年底和2006年底的住房面積 ;
(2)求2024年底的住房面積.(計算結果以萬平方米為單位,且精確到0.01)
[解](1)
(2)
|
第2小題滿分6分,第3小題滿分7分.
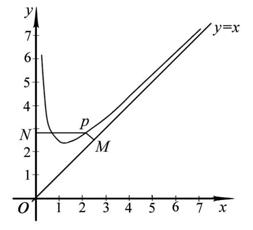 已知函數
已知函數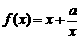 的定義域為
的定義域為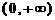 ,且
,且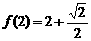 . 設點
. 設點 是函數圖象上的任意一點,過點
是函數圖象上的任意一點,過點 分別作直線
分別作直線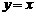 和
和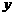 軸的垂線,垂足分別為
軸的垂線,垂足分別為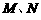 .
.
(1)求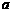 的值;
的值;
(2)問: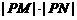 是否為定值?若是,則求出該定值,若不是,則說明理由;
是否為定值?若是,則求出該定值,若不是,則說明理由;
(3)設 為坐標原點,求四邊形
為坐標原點,求四邊形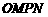 面積的最小值.
面積的最小值.
[解](1)
(2)
(3)
|
第2小題滿分8分. 第3小題滿分5分.
(1)求右焦點坐標是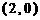 ,且經過點
,且經過點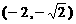 的橢圓的標準方程;
的橢圓的標準方程;
(2)已知橢圓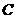 的方程是
的方程是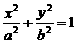
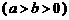 . 設斜率為
. 設斜率為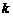 的直線
的直線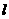 ,交橢圓
,交橢圓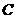 于
于
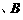 兩點,
兩點, 的中點為
的中點為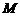 . 證明:當直線
. 證明:當直線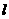 平行移動時,動點
平行移動時,動點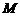 在一條過原點的定直線上;
在一條過原點的定直線上;
(3)利用(2)所揭示的橢圓幾何性質,用作圖方法找出下面給定橢圓的中心,簡要寫出作圖步驟,并在圖中標出橢圓的中心.
 [解](1)
[解](1)
[證明](2)
[解](3)
普通高等學校春季招生考試
16. 設函數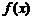 的定義域為
的定義域為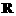 ,有下列三個命題:
,有下列三個命題:
(1)若存在常數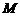 ,使得對任意
,使得對任意 ,有
,有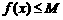 ,則
,則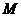 是函數
是函數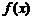 的最大值;
的最大值;
(2)若存在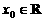 ,使得對任意
,使得對任意 ,且
,且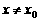 ,有
,有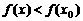 ,則
,則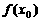 是函數
是函數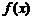
的最大值;
(3)若存在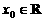 ,使得對任意
,使得對任意 ,有
,有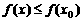 ,則
,則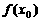 是函數
是函數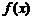 的最大值.
的最大值.
這些命題中,真命題的個數是
(A)0個. (B)1個. (C)2個. (D)3個.
[答] ( )
15. 若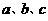 是常數,則“
是常數,則“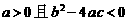 ”是“對任意
”是“對任意 ,有
,有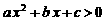 ”
”
的
(A)充分不必要條件. (B)必要不充分條件.
(C)充要條件. (D)既不充分也不必要條件.
[答] ( )
14. 在△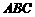 中,若
中,若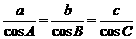 ,則△
,則△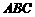 是
是
(A)直角三角形. (B)等邊三角形.
(C)鈍角三角形. (D)等腰直角三角形.
[答] ( )
13. 已知直線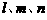 及平面
及平面 ,下列命題中的假命題是
,下列命題中的假命題是
(A)若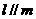 ,
,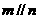 ,則
,則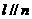 . (B)若
. (B)若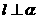 ,
,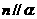 ,則
,則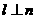 .
.
(C)若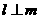 ,
,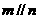 ,則
,則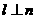 . (D)若
. (D)若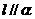 ,
,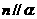 ,則
,則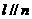 .
.
[答] ( )
12. 已知函數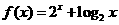 ,數列
,數列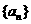 的通項公式是
的通項公式是 (
(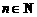 ),當
),當
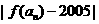 取得最小值時,
取得最小值時,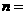 .
.
|
四個結論,其中有且只有一個結論是正確的,必須把正確結論的
代號寫在題后的圓括號內,選對得 4分,否則一律得零分.
11. 函數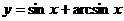 的值域是
.
的值域是
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com