
題目列表(包括答案和解析)
(17)(本大題滿分12分)已知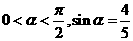
(Ⅰ)求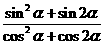 的值;
的值;
(Ⅱ)求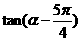 的值。
的值。
解:(Ⅰ)由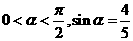 ,得
,得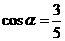 ,所以
,所以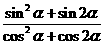 =
=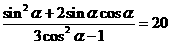 。
。
(Ⅱ)∵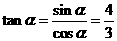 ,∴
,∴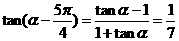 。
。
(18)(本大題滿分12分)在添加劑的搭配使用中,為了找到最佳的搭配方案,需要對各種不同的搭配方式作比較。在試制某種牙膏新品種時,需要選用兩種不同的添加劑。現有芳香度分別為0,1,2,3,4,5的六種添加劑可供選用。根據試驗設計原理,通常首先要隨機選取兩種不同的添加劑進行搭配試驗。
(Ⅰ)求所選用的兩種不同的添加劑的芳香度之和等于4的概率;
(Ⅱ)求所選用的兩種不同的添加劑的芳香度之和不小于3的概率;
解:設“所選用的兩種不同的添加劑的芳香度之和等于4”的事件為A,“所選用的兩種不同的添加劑的芳香度之和不小于3”的事件為B
 (Ⅰ)芳香度之和等于4的取法有2種:
(Ⅰ)芳香度之和等于4的取法有2種: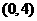 、
、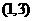 ,故
,故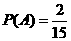 。
。
(Ⅱ)芳香度之和等于1的取法有1種: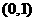 ;芳香度之和等于2的取法有1種:
;芳香度之和等于2的取法有1種: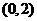 ,故
,故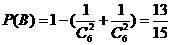 。
。
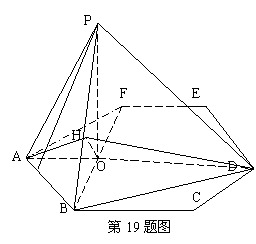
(19)(本大題滿分12分)如圖,P是邊長為1的正六邊形ABCDEF所在平面外一點,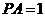 ,P在平面ABC內的射影為BF的中點O。
,P在平面ABC內的射影為BF的中點O。
(Ⅰ)證明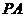 ⊥
⊥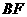 ;
;
(Ⅱ)求面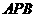 與面
與面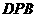 所成二面角的大小。
所成二面角的大小。
解:(Ⅰ)在正六邊形ABCDEF中,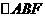 為等腰三角形,
為等腰三角形,
∵P在平面ABC內的射影為O,∴PO⊥平面ABF,∴AO為PA在平面ABF內的射影;∵O為BF中點,∴AO⊥BF,∴PA⊥BF。
(Ⅱ)∵PO⊥平面ABF,∴平面PBF⊥平面ABC;而O為BF中點,ABCDEF是正六邊形 ,∴A、O、D共線,且直線AD⊥BF,則AD⊥平面PBF;又∵正六邊形ABCDEF的邊長為1,∴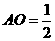 ,
,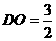 ,
,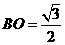 。
。
過O在平面POB內作OH⊥PB于H,連AH、DH,則AH⊥PB,DH⊥PB,所以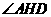 為所求二面角平面角。
為所求二面角平面角。
在 中,OH=
中,OH=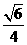 ,
,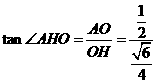 =
=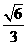 。
。
在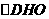 中,
中,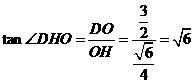 ;
;
而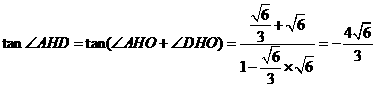
(Ⅱ)以O為坐標原點,建立空間直角坐標系,P(0,0,1),A(0,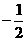 ,0),B(
,0),B(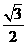 ,0,0),D(0,2,0),∴
,0,0),D(0,2,0),∴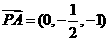 ,
,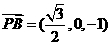 ,
,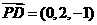
設平面PAB的法向量為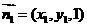 ,則
,則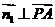 ,
,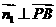 ,得
,得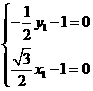 ,
,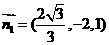 ;
;
設平面PDB的法向量為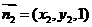 ,則
,則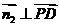 ,
,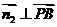 ,得
,得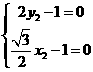 ,
,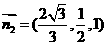 ;
;
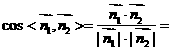
(20)(本大題滿分12分)設函數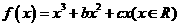 ,已知
,已知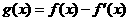 是奇函數。
是奇函數。
(Ⅰ)求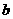 、
、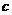 的值。
的值。
(Ⅱ)求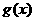 的單調區間與極值。
的單調區間與極值。
證明(Ⅰ)∵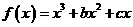 ,∴
,∴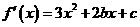 。從而
。從而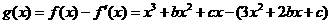 =
=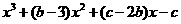 是一個奇函數,所以
是一個奇函數,所以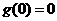 得
得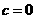 ,由奇函數定義得
,由奇函數定義得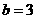 ;
;
(Ⅱ)由(Ⅰ)知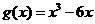 ,從而
,從而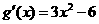 ,由此可知,
,由此可知,
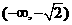 和
和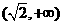 是函數
是函數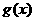 是單調遞增區間;
是單調遞增區間;
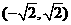 是函數
是函數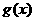 是單調遞減區間;
是單調遞減區間;
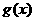 在
在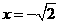 時,取得極大值,極大值為
時,取得極大值,極大值為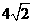 ,
,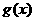 在
在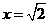 時,取得極小值,極小值為
時,取得極小值,極小值為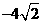 。
。
(21)(本大題滿分12分)在等差數列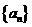 中,
中,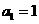 ,前
,前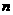 項和
項和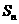 滿足條件
滿足條件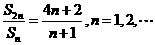 ,
,
(Ⅰ)求數列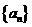 的通項公式;
的通項公式;
(Ⅱ)記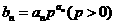 ,求數列
,求數列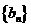 的前
的前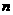 項和
項和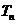 。
。
解:(Ⅰ)設等差數列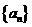 的公差為
的公差為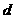 ,由
,由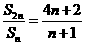 得:
得: ,所以
,所以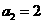 ,即
,即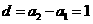 ,又
,又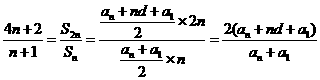 =
=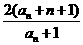 ,所以
,所以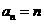 。
。
(Ⅱ)由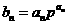 ,得
,得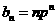 。所以
。所以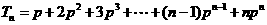 ,
,
當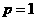 時,
時,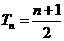 ;
;
當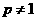 時,
時,
 ,
,

即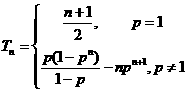 。
。
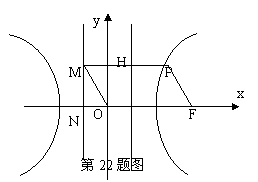
(22)(本大題滿分14分)如圖,F為雙曲線C: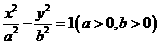 的右焦點。P為雙曲線C右支上一點,且位于
的右焦點。P為雙曲線C右支上一點,且位于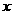 軸上方,M為左準線上一點,
軸上方,M為左準線上一點, 為坐標原點。已知四邊形
為坐標原點。已知四邊形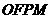 為平行四邊形,
為平行四邊形,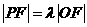 。
。
 (Ⅰ)寫出雙曲線C的離心率
(Ⅰ)寫出雙曲線C的離心率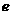 與
與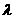 的關系式;
的關系式;
(Ⅱ)當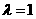 時,經過焦點F且平行于OP的直線交雙曲線于A、B點,若
時,經過焦點F且平行于OP的直線交雙曲線于A、B點,若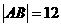 ,求此時的雙曲線方程。
,求此時的雙曲線方程。
解:∵四邊形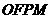 是
是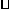 ,∴
,∴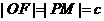 ,作雙曲線的右準線交PM于H,則
,作雙曲線的右準線交PM于H,則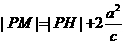 ,又
,又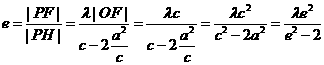 ,
,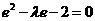 。
。
(Ⅱ)當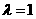 時,
時,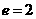 ,
,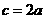 ,
,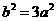 ,雙曲線為
,雙曲線為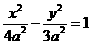 ,設P
,設P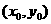 ,則
,則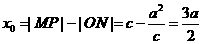 ,
,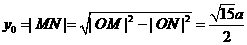 ,所以直線OP的斜率為
,所以直線OP的斜率為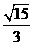 ,則直線AB的方程為
,則直線AB的方程為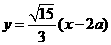 ,代入到雙曲線方程得:
,代入到雙曲線方程得: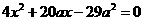 ,
,
又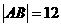 ,由
,由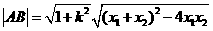 得:
得: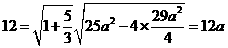 ,解得
,解得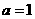 ,則
,則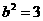 ,所以
,所以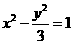 為所求。
為所求。
(13)設常數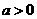 ,
,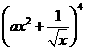 展開式中
展開式中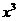 的系數為
的系數為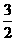 ,則
,則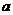 =_____。
=_____。
解: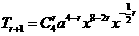 ,由
,由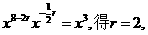
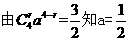 。
。
(14)在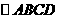 中,
中,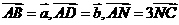 ,M為BC的中點,則
,M為BC的中點,則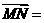 _______。(用
_______。(用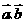 表示)
表示)
解: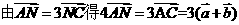 ,
,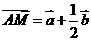 ,所以
,所以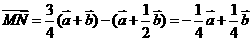 。
。
(15)函數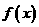 對于任意實數
對于任意實數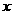 滿足條件
滿足條件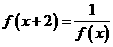 ,若
,若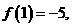 則
則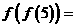 __________。
__________。
解:由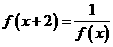 得
得 ,所以
,所以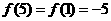 ,則
,則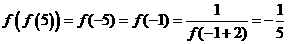 。
。
(16)平行四邊形的一個頂點A在平面 內,其余頂點在
內,其余頂點在 的同側,已知其中有兩個頂點到
的同側,已知其中有兩個頂點到 的距離分別為1和2 ,那么剩下的一個頂點到平面
的距離分別為1和2 ,那么剩下的一個頂點到平面 的距離可能是:
的距離可能是:
①1; ②2; ③3; ④4;
以上結論正確的為______________。(寫出所有正確結論的編號)
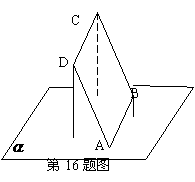 解:如圖,B、D到平面
解:如圖,B、D到平面 的距離為1、2,則D、B的中點到平面
的距離為1、2,則D、B的中點到平面 的距離為
的距離為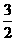 ,所以C到平面
,所以C到平面 的距離為3;
的距離為3;
B、C到平面 的距離為1、2,D到平面
的距離為1、2,D到平面 的距離為
的距離為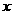 ,則
,則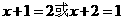 ,即
,即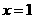 ,所以D到平面
,所以D到平面 的距離為1;
的距離為1;
C、D到平面 的距離為1、2,同理可得B到平面
的距離為1、2,同理可得B到平面 的距離為1;所以選①③。
的距離為1;所以選①③。
(1)設全集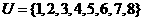 ,集合
,集合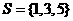 ,
,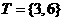 ,則
,則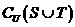 等于( )
等于( )
A.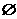 B.
B.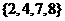 C.
C.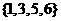 D.
D.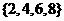
解: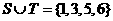 ,則
,則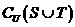 =
=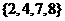 ,故選B
,故選B
(2)不等式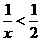 的解集是( )
的解集是( )
A.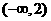 B.
B.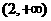 C.
C.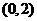 D.
D.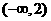
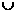
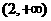
解:由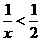 得:
得: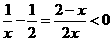 ,即
,即 ,故選D。
,故選D。
(3)函數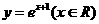 的反函數是( )
的反函數是( )
A. B.
B.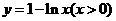
C.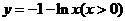 D.
D.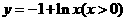
解:由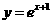 得:
得: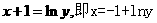 ,所以
,所以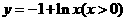 為所求,故選D。
為所求,故選D。
(4)“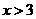 ”是
”是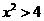 “的( )
“的( )
A.必要不充分條件 B.充分不必要條件
C.充分必要條件 D.既不充分也不必要條件
解:條件集是結論集的子集,所以選B。
(5)若拋物線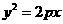 的焦點與橢圓
的焦點與橢圓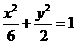 的右焦點重合,則
的右焦點重合,則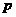 的值為( )
的值為( )
A.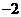 B.
B.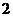 C.
C.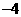 D.
D.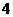
解:橢圓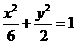 的右焦點為(2,0),所以拋物線
的右焦點為(2,0),所以拋物線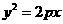 的焦點為(2,0),則
的焦點為(2,0),則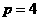 ,故選D。
,故選D。
(6)表面積為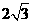 的正八面體的各個頂點都在同一個球面上,則此球的體積為
的正八面體的各個頂點都在同一個球面上,則此球的體積為
A.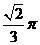 B.
B.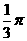 C.
C.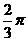 D.
D.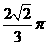
解:此正八面體是每個面的邊長均為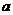 的正三角形,所以由
的正三角形,所以由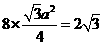 知,
知,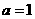 ,則此球的直徑為
,則此球的直徑為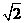 ,故選A。
,故選A。
(7)直線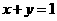 與圓
與圓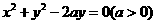 沒有公共點,則
沒有公共點,則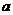 的取值范圍是
的取值范圍是
A. B.
B.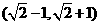 C.
C.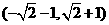 D.
D.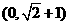
解:由圓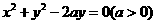 的圓心
的圓心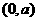 到直線
到直線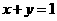 大于
大于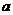 ,且
,且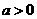 ,選A。
,選A。
(8)對于函數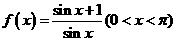 ,下列結論正確的是( )
,下列結論正確的是( )
A.有最大值而無最小值 B.有最小值而無最大值
C.有最大值且有最小值 D.既無最大值又無最小值
解:令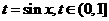 ,則函數
,則函數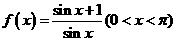 的值域為函數
的值域為函數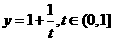 的值域,而
的值域,而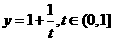 是一個減函減,故選B。
是一個減函減,故選B。
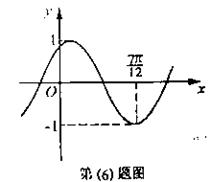 (9)將函數
(9)將函數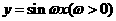 的圖象按向量
的圖象按向量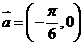 平移,平移后的圖象如圖所示,則平移后的圖象所對應函數的解析式是( )
平移,平移后的圖象如圖所示,則平移后的圖象所對應函數的解析式是( )
A.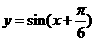 B.
B.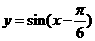
C.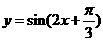 D.
D.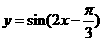
解:將函數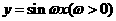 的圖象按向量
的圖象按向量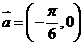 平移,平移后的圖象所對應的解析式為
平移,平移后的圖象所對應的解析式為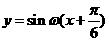 ,由圖象知,
,由圖象知,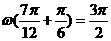 ,所以
,所以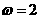 ,因此選C。
,因此選C。
(10)如果實數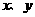 滿足條件
滿足條件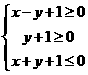 ,那么
,那么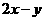 的最大值為( )
的最大值為( )
A.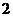 B.
B.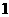 C.
C.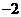 D.
D.
解:當直線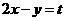 過點(0,-1)時,
過點(0,-1)時,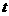 最大,故選B。
最大,故選B。
(11)如果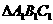 的三個內角的余弦值分別等于
的三個內角的余弦值分別等于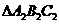 的三個內角的正弦值,則( )
的三個內角的正弦值,則( )
A.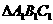 和
和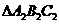 都是銳角三角形 B.
都是銳角三角形 B.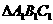 和
和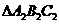 都是鈍角三角形
都是鈍角三角形
C.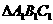 是鈍角三角形,
是鈍角三角形,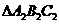 是銳角三角形
是銳角三角形
D.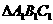 是銳角三角形,
是銳角三角形,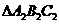 是鈍角三角形
是鈍角三角形
解: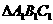 的三個內角的余弦值均大于0,則
的三個內角的余弦值均大于0,則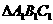 是銳角三角形,若
是銳角三角形,若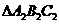 是銳角三角形,由
是銳角三角形,由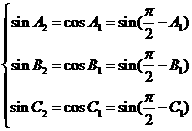 ,得
,得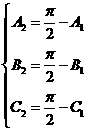 ,那么,
,那么,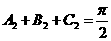 ,所以
,所以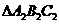 是鈍角三角形。故選D。
是鈍角三角形。故選D。
(12)在正方體上任選3個頂點連成三角形,則所得的三角形是直角非等腰三角形的概率為( )
A.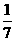 B.
B.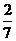 C.
C.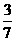 D.
D.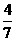
解:在正方體上任選3個頂點連成三角形可得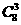 個三角形,要得直角非等腰三角形,則每個頂點上可得三個(即正方體的一邊與過此點的一條面對角線),共有24個,得
個三角形,要得直角非等腰三角形,則每個頂點上可得三個(即正方體的一邊與過此點的一條面對角線),共有24個,得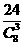 ,所以選C。
,所以選C。
2006年普通高等學校招生全國統一考試(安徽卷)理科數學
第Ⅱ卷(非選擇題 共90分)
請用0.5毫米黑色墨水簽字筆在答題卡上書寫作答,在試題卷上書寫作答無效。
15.設F是橢圓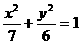 的右焦點,且橢圓上至少有21個不同的點Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…組成公差為d的等差數列,則d的取值范圍為
.
的右焦點,且橢圓上至少有21個不同的點Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…組成公差為d的等差數列,則d的取值范圍為
.
14.若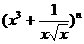 的展開式中的常數項為84,則n=
.
的展開式中的常數項為84,則n=
.
13.同時拋物線兩枚相同的均勻硬幣,隨機變量ξ=1表示結果中有正面向上,ξ=0表示結果中沒有正面向上,則Eξ= .
12.已知向量a=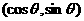 ,向量b=
,向量b=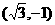 ,則|2a-b|的最大值是
.
,則|2a-b|的最大值是
.
11.設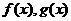 分別是定義在R上的奇函數和偶函數,當
分別是定義在R上的奇函數和偶函數,當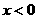 時,
時,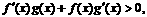
且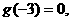 則不等式
則不等式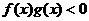 的解集是________________________.
的解集是________________________.
10.從正方體的八個頂點中任取三個點為頂點作三角形,其中直角三角形的個數為( )
A.56 B.52 C.48 D.40
9.設集合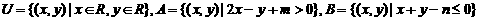 ,那么點P(2,3)
,那么點P(2,3) (
(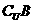 )的充要條件是 ( )
)的充要條件是 ( )
A.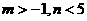 B.
B.
C.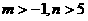 D.
D.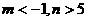
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com